第七十九课 最短路径(Floyd)







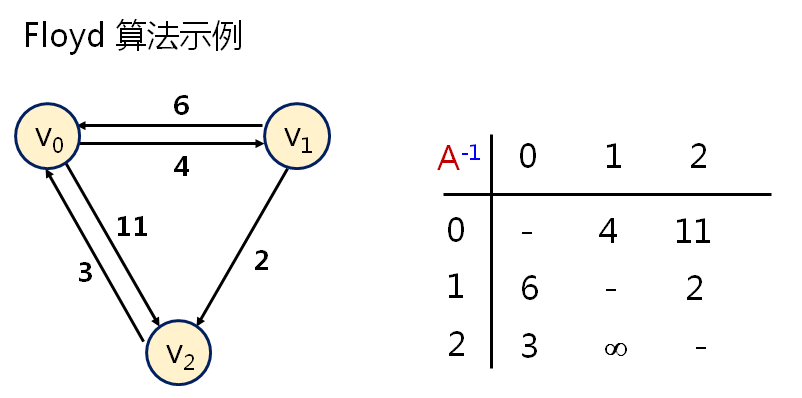
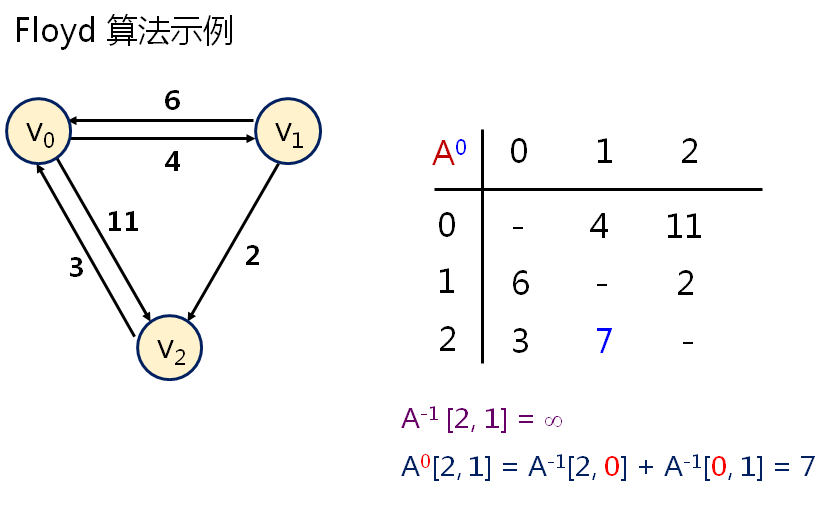
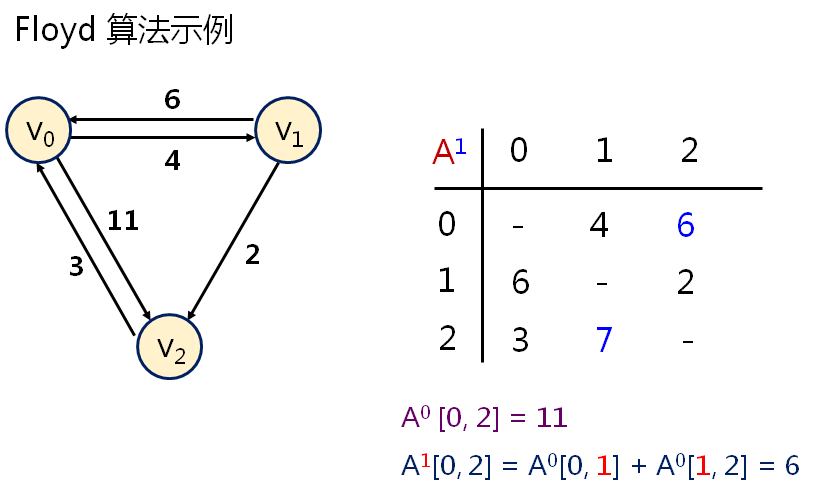
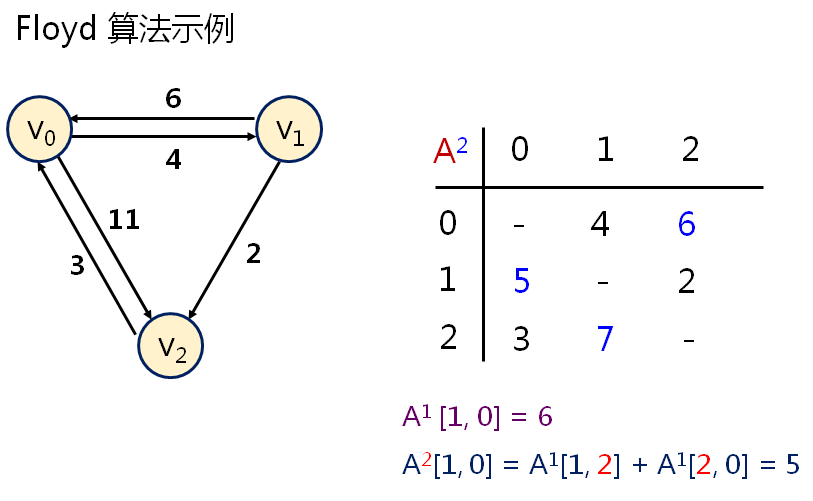



程序如下:
#ifndef GRAPH_H
#define GRAPH_H #include "Object.h"
#include "SharedPointer.h"
#include "Array.h"
#include "DynamicArray.h"
#include "LinkQueue.h"
#include "LinkStack.h"
#include "Sort.h" namespace DTLib
{ template < typename E >
struct Edge : public Object
{
int b;
int e;
E data; Edge(int i=-, int j=-)
{
b = i;
e = j;
} Edge(int i, int j, const E& value)
{
b = i;
e = j;
data = value;
} bool operator == (const Edge<E>& obj)
{
return (b == obj.b) && (e == obj.e); //在这里不关注权值大小
} bool operator != (const Edge<E>& obj)
{
return !(*this == obj);
} bool operator < (const Edge<E>& obj)
{
return (data < obj.data);
} bool operator > (const Edge<E>& obj)
{
return (data > obj.data);
}
}; template < typename V, typename E >
class Graph : public Object
{
protected:
template < typename T >
DynamicArray<T>* toArray(LinkQueue<T>& queue)
{
DynamicArray<T>* ret = new DynamicArray<T>(queue.length()); if( ret != NULL )
{
for(int i=; i<ret->length(); i++, queue.remove())
{
ret->set(i, queue.front());
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create ret object...");
} return ret;
} SharedPointer< Array<Edge<E> > > getUndirectedEdges()
{
DynamicArray<Edge<E>>* ret = NULL; if( asUndirected() )
{
LinkQueue<Edge<E>> queue; for(int i=; i<vCount(); i++)
{
for(int j=i; j<vCount(); j++)
{
if( isAdjacent(i, j) )
{
queue.add(Edge<E>(i, j, getEdge(i, j)));
}
}
} ret = toArray(queue);
}
else
{
THROW_EXCEPTION(InvalidOperationException, "This function is for undirected graph only...");
} return ret;
} int find(Array<int>& p, int v)
{
while( p[v] != -)
{
v = p[v];
} return v;
}
public:
virtual V getVertex(int i) = ;
virtual bool getVertex(int i, V& value) = ;
virtual bool setVertex(int i, const V& value) = ;
virtual SharedPointer< Array<int> > getAdjacent(int i) = ;
virtual bool isAdjacent(int i, int j) = ;
virtual E getEdge(int i, int j) = ;
virtual bool getEdge(int i, int j, E& value) = ;
virtual bool setEdge(int i, int j, const E& value) = ;
virtual bool removeEdge(int i, int j) = ;
virtual int vCount() = ;
virtual int eCount() = ;
virtual int OD(int i) = ;
virtual int ID(int i) = ; virtual int TD(int i)
{
return ID(i) + OD(i);
} bool asUndirected()
{
bool ret = true; for(int i=; i<vCount(); i++)
{
for(int j=; j<vCount(); j++)
{
if( isAdjacent(i, j) )
{
ret = ret && isAdjacent(j, i) && (getEdge(i, j) == getEdge(j, i));
}
}
} return ret;
} SharedPointer< Array< Edge<E > > > prim(const E& LIMIT, const bool MINIUM = true) //参数为理论上的最大权值
{
LinkQueue< Edge<E> > ret; if( asUndirected() )
{
DynamicArray<int> adjVex(vCount());
DynamicArray<bool> mark(vCount());
DynamicArray<E> cost(vCount());
SharedPointer< Array<int> > aj = NULL;
bool end = false;
int v = ; for(int i=; i<vCount(); i++)
{
adjVex[i] = -;
mark[i] = false;
cost[i] = LIMIT;
} mark[v] = true; aj = getAdjacent(v); for(int j=; j<aj->length(); j++)
{
cost[(*aj)[j]] = getEdge(v, (*aj)[j]);
adjVex[(*aj)[j]] = v;
} for(int i=; (i<vCount()) && !end; i++)
{
E m = LIMIT;
int k = -; for(int j=; j<vCount(); j++)
{
if( !mark[j] && (MINIUM ? (cost[j] < m) : (cost[j] > m)))
{
m = cost[j];
k = j;
}
} end = (k == -); if( !end )
{
ret.add(Edge<E>(adjVex[k], k, getEdge(adjVex[k], k))); mark[k] = true; aj = getAdjacent(k); for(int j=; j<aj->length(); j++)
{
if( !mark[(*aj)[j]] && (MINIUM ? (getEdge(k, (*aj)[j]) < cost[(*aj)[j]]) : (getEdge(k, (*aj)[j]) > cost[(*aj)[j]])) )
{
cost[(*aj)[j]] = getEdge(k, (*aj)[j]);
adjVex[(*aj)[j]] = k;
}
}
}
}
}
else
{
THROW_EXCEPTION(InvalidOperationException, "Prim operator is for undirected graph only...");
} if( ret.length() != (vCount() - ) )
{
THROW_EXCEPTION(InvalidOperationException, "No enough edge for prim operation...");
} return toArray(ret);
} SharedPointer< Array<Edge<E> > > kruskal(const bool MINMUM = true)
{
LinkQueue< Edge<E> > ret; SharedPointer< Array< Edge<E> > > edges = getUndirectedEdges(); DynamicArray<int> p(vCount()); //前驱标记数组 for(int i=; i<p.length(); i++)
{
p[i] = -;
} Sort::Shell(*edges, MINMUM); for(int i=; (i<edges->length()) && (ret.length() < (vCount() - )); i++)
{
int b = find(p, (*edges)[i].b);
int e = find(p, (*edges)[i].e); if( b != e )
{
p[e] = b; ret.add((*edges)[i]);
}
} if( ret.length() != (vCount() - ) )
{
THROW_EXCEPTION(InvalidOperationException, "No enough edges for Kruskal operation...");
} return toArray(ret);
} SharedPointer< Array<int> > BFS(int i)
{
DynamicArray<int>* ret = NULL; if( ( <= i) && (i < vCount()) )
{
LinkQueue<int> q;
LinkQueue<int> r;
DynamicArray<bool> visited(vCount()); for(int i=; i<visited.length(); i++)
{
visited[i] = false;
} q.add(i); while( q.length() > )
{
int v = q.front(); q.remove(); if( !visited[v] )
{
SharedPointer< Array<int> > aj = getAdjacent(v); for(int j=; j<aj->length(); j++)
{
q.add((*aj)[j]);
} r.add(v); visited[v] = true;
}
} ret = toArray(r);
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Index i is invalid...");
} return ret;
} SharedPointer< Array<int> > DFS(int i)
{
DynamicArray<int>* ret = NULL; if( ( <= i) && (i < vCount()) )
{
LinkStack<int> s;
LinkQueue<int> r;
DynamicArray<bool> visited(vCount()); for(int j=; j<visited.length(); j++)
{
visited[j] = false;
} s.push(i); while( s.size() > )
{
int v = s.top(); s.pop(); if( !visited[v] )
{
SharedPointer< Array<int> > aj = getAdjacent(v); for(int j=aj->length() - ; j>=; j--)
{
s.push((*aj)[j]);
} r.add(v); visited[v] = true;
}
} ret = toArray(r);
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Index i is invalid...");
} return ret;
} SharedPointer<Array<int>> dijkstra(int i, int j, const E& LIMIT)
{
LinkQueue<int> ret; if( ( <= i) && (i < vCount()) && ( <= j) && (j < vCount()) )
{
DynamicArray<E> dist(vCount());
DynamicArray<int> path(vCount());
DynamicArray<bool> mark(vCount()); for(int k=; k<vCount(); k++)
{
mark[k] = false;
path[k] = -; dist[k] = isAdjacent(i, k) ? (path[k] = i, getEdge(i, k)) : LIMIT;
} mark[i] = true; for(int k=; k<vCount(); k++)
{
E m = LIMIT;
int u = -; for(int w=; w<vCount(); w++)
{
if( !mark[w] && (dist[w] < m) )
{
m = dist[w];
u = w;
}
} if( u == - )
{
break;
} mark[u] = true; for(int w=; w<vCount(); w++)
{
if( !mark[w] && isAdjacent(u, w) && (dist[u] + getEdge(u, w) < dist[w]) )
{
dist[w] = dist[u] + getEdge(u, w);
path[w] = u;
}
}
} LinkStack<int> s; s.push(j); for(int k=path[j]; k != -; k=path[k])
{
s.push(k);
} while( s.size() > )
{
ret.add(s.top()); s.pop();
}
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Index<i, j> is invalid...");
} if( ret.length() < )
{
THROW_EXCEPTION(ArithmeticException, "There is no path grom i to j...");
} return toArray(ret);
} int floyd(int x, int y, const E& LIMIT)
{
int ret = -; if( ( <= x) && (x < vCount()) && ( <= y) && ( y < vCount()) )
{
DynamicArray< DynamicArray<E> > dist(vCount()); for(int k=; k<vCount(); k++)
{
dist[k].resize(vCount());
} for(int i = ; i<vCount(); i++)
{
for(int j=; j<vCount(); j++)
{
dist[i][j] = isAdjacent(i, j) ? getEdge(i, j) : LIMIT;
}
} for(int k=; k<vCount(); k++)
{
for(int i = ; i<vCount(); i++)
{
for(int j=; j<vCount(); j++)
{
if( (dist[i][k] + dist[k][j]) < dist[i][j] )
{
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
} ret = dist[x][y]; }
else
{
THROW_EXCEPTION(ArithmeticException, "Index<x, y> is invalid...");
} return ret;
}
}; } #endif // GRAPH_H
测试程序如下:
#include <iostream>
#include "MatrixGraph.h"
#include "ListGraph.h" using namespace std;
using namespace DTLib; template< typename V, typename E >
Graph<V, E>& GraphEasy()
{
static MatrixGraph<, V, E> g; g.setEdge(, , );
g.setEdge(, , );
g.setEdge(, , );
g.setEdge(, , );
g.setEdge(, , ); return g;
} template< typename V, typename E >
Graph<V, E>& GraphComplex()
{
static ListGraph<V, E> g(); g.setEdge(, , );
g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , ); g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); return g;
} template< typename V, typename E >
Graph<V, E>& GraphSample()
{
static ListGraph<V, E> g(); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , ); return g;
} int main()
{
Graph<int, int>& g = GraphSample<int, int>();
//int r = g.floyd(0, 2, 65536); for(int i=; i<g.vCount();i++)
{
for(int j=; j<g.vCount(); j++)
{
cout << g.floyd(i, j, ) << " ";
} cout << endl;
} cout << endl;
return ;
}
结果如下:


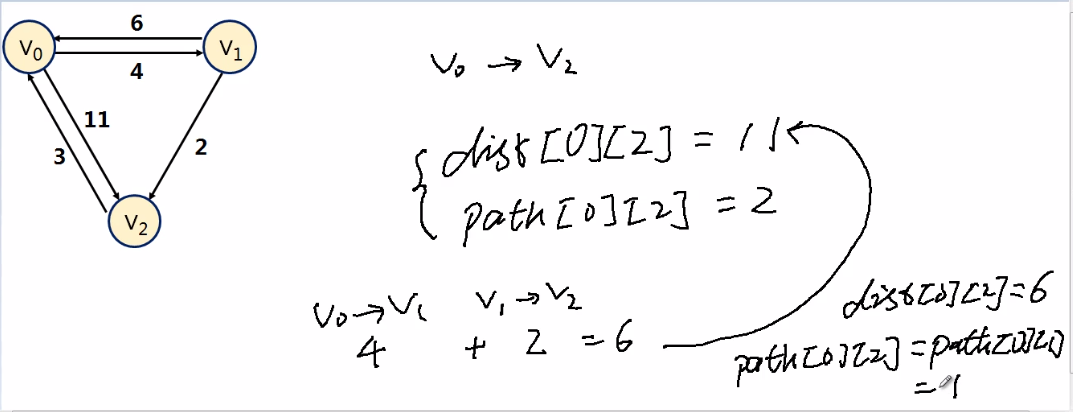
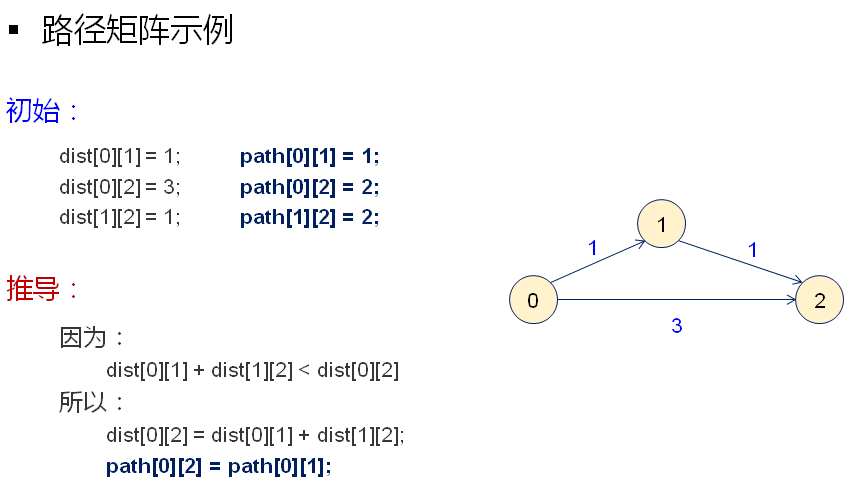

程序改进如下:
#ifndef GRAPH_H
#define GRAPH_H #include "Object.h"
#include "SharedPointer.h"
#include "Array.h"
#include "DynamicArray.h"
#include "LinkQueue.h"
#include "LinkStack.h"
#include "Sort.h" namespace DTLib
{ template < typename E >
struct Edge : public Object
{
int b;
int e;
E data; Edge(int i=-, int j=-)
{
b = i;
e = j;
} Edge(int i, int j, const E& value)
{
b = i;
e = j;
data = value;
} bool operator == (const Edge<E>& obj)
{
return (b == obj.b) && (e == obj.e); //在这里不关注权值大小
} bool operator != (const Edge<E>& obj)
{
return !(*this == obj);
} bool operator < (const Edge<E>& obj)
{
return (data < obj.data);
} bool operator > (const Edge<E>& obj)
{
return (data > obj.data);
}
}; template < typename V, typename E >
class Graph : public Object
{
protected:
template < typename T >
DynamicArray<T>* toArray(LinkQueue<T>& queue)
{
DynamicArray<T>* ret = new DynamicArray<T>(queue.length()); if( ret != NULL )
{
for(int i=; i<ret->length(); i++, queue.remove())
{
ret->set(i, queue.front());
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create ret object...");
} return ret;
} SharedPointer< Array<Edge<E> > > getUndirectedEdges()
{
DynamicArray<Edge<E>>* ret = NULL; if( asUndirected() )
{
LinkQueue<Edge<E>> queue; for(int i=; i<vCount(); i++)
{
for(int j=i; j<vCount(); j++)
{
if( isAdjacent(i, j) )
{
queue.add(Edge<E>(i, j, getEdge(i, j)));
}
}
} ret = toArray(queue);
}
else
{
THROW_EXCEPTION(InvalidOperationException, "This function is for undirected graph only...");
} return ret;
} int find(Array<int>& p, int v)
{
while( p[v] != -)
{
v = p[v];
} return v;
}
public:
virtual V getVertex(int i) = ;
virtual bool getVertex(int i, V& value) = ;
virtual bool setVertex(int i, const V& value) = ;
virtual SharedPointer< Array<int> > getAdjacent(int i) = ;
virtual bool isAdjacent(int i, int j) = ;
virtual E getEdge(int i, int j) = ;
virtual bool getEdge(int i, int j, E& value) = ;
virtual bool setEdge(int i, int j, const E& value) = ;
virtual bool removeEdge(int i, int j) = ;
virtual int vCount() = ;
virtual int eCount() = ;
virtual int OD(int i) = ;
virtual int ID(int i) = ; virtual int TD(int i)
{
return ID(i) + OD(i);
} bool asUndirected()
{
bool ret = true; for(int i=; i<vCount(); i++)
{
for(int j=; j<vCount(); j++)
{
if( isAdjacent(i, j) )
{
ret = ret && isAdjacent(j, i) && (getEdge(i, j) == getEdge(j, i));
}
}
} return ret;
} SharedPointer< Array< Edge<E > > > prim(const E& LIMIT, const bool MINIUM = true) //参数为理论上的最大权值
{
LinkQueue< Edge<E> > ret; if( asUndirected() )
{
DynamicArray<int> adjVex(vCount());
DynamicArray<bool> mark(vCount());
DynamicArray<E> cost(vCount());
SharedPointer< Array<int> > aj = NULL;
bool end = false;
int v = ; for(int i=; i<vCount(); i++)
{
adjVex[i] = -;
mark[i] = false;
cost[i] = LIMIT;
} mark[v] = true; aj = getAdjacent(v); for(int j=; j<aj->length(); j++)
{
cost[(*aj)[j]] = getEdge(v, (*aj)[j]);
adjVex[(*aj)[j]] = v;
} for(int i=; (i<vCount()) && !end; i++)
{
E m = LIMIT;
int k = -; for(int j=; j<vCount(); j++)
{
if( !mark[j] && (MINIUM ? (cost[j] < m) : (cost[j] > m)))
{
m = cost[j];
k = j;
}
} end = (k == -); if( !end )
{
ret.add(Edge<E>(adjVex[k], k, getEdge(adjVex[k], k))); mark[k] = true; aj = getAdjacent(k); for(int j=; j<aj->length(); j++)
{
if( !mark[(*aj)[j]] && (MINIUM ? (getEdge(k, (*aj)[j]) < cost[(*aj)[j]]) : (getEdge(k, (*aj)[j]) > cost[(*aj)[j]])) )
{
cost[(*aj)[j]] = getEdge(k, (*aj)[j]);
adjVex[(*aj)[j]] = k;
}
}
}
}
}
else
{
THROW_EXCEPTION(InvalidOperationException, "Prim operator is for undirected graph only...");
} if( ret.length() != (vCount() - ) )
{
THROW_EXCEPTION(InvalidOperationException, "No enough edge for prim operation...");
} return toArray(ret);
} SharedPointer< Array<Edge<E> > > kruskal(const bool MINMUM = true)
{
LinkQueue< Edge<E> > ret; SharedPointer< Array< Edge<E> > > edges = getUndirectedEdges(); DynamicArray<int> p(vCount()); //前驱标记数组 for(int i=; i<p.length(); i++)
{
p[i] = -;
} Sort::Shell(*edges, MINMUM); for(int i=; (i<edges->length()) && (ret.length() < (vCount() - )); i++)
{
int b = find(p, (*edges)[i].b);
int e = find(p, (*edges)[i].e); if( b != e )
{
p[e] = b; ret.add((*edges)[i]);
}
} if( ret.length() != (vCount() - ) )
{
THROW_EXCEPTION(InvalidOperationException, "No enough edges for Kruskal operation...");
} return toArray(ret);
} SharedPointer< Array<int> > BFS(int i)
{
DynamicArray<int>* ret = NULL; if( ( <= i) && (i < vCount()) )
{
LinkQueue<int> q;
LinkQueue<int> r;
DynamicArray<bool> visited(vCount()); for(int i=; i<visited.length(); i++)
{
visited[i] = false;
} q.add(i); while( q.length() > )
{
int v = q.front(); q.remove(); if( !visited[v] )
{
SharedPointer< Array<int> > aj = getAdjacent(v); for(int j=; j<aj->length(); j++)
{
q.add((*aj)[j]);
} r.add(v); visited[v] = true;
}
} ret = toArray(r);
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Index i is invalid...");
} return ret;
} SharedPointer< Array<int> > DFS(int i)
{
DynamicArray<int>* ret = NULL; if( ( <= i) && (i < vCount()) )
{
LinkStack<int> s;
LinkQueue<int> r;
DynamicArray<bool> visited(vCount()); for(int j=; j<visited.length(); j++)
{
visited[j] = false;
} s.push(i); while( s.size() > )
{
int v = s.top(); s.pop(); if( !visited[v] )
{
SharedPointer< Array<int> > aj = getAdjacent(v); for(int j=aj->length() - ; j>=; j--)
{
s.push((*aj)[j]);
} r.add(v); visited[v] = true;
}
} ret = toArray(r);
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Index i is invalid...");
} return ret;
} SharedPointer<Array<int>> dijkstra(int i, int j, const E& LIMIT)
{
LinkQueue<int> ret; if( ( <= i) && (i < vCount()) && ( <= j) && (j < vCount()) )
{
DynamicArray<E> dist(vCount());
DynamicArray<int> path(vCount());
DynamicArray<bool> mark(vCount()); for(int k=; k<vCount(); k++)
{
mark[k] = false;
path[k] = -; dist[k] = isAdjacent(i, k) ? (path[k] = i, getEdge(i, k)) : LIMIT;
} mark[i] = true; for(int k=; k<vCount(); k++)
{
E m = LIMIT;
int u = -; for(int w=; w<vCount(); w++)
{
if( !mark[w] && (dist[w] < m) )
{
m = dist[w];
u = w;
}
} if( u == - )
{
break;
} mark[u] = true; for(int w=; w<vCount(); w++)
{
if( !mark[w] && isAdjacent(u, w) && (dist[u] + getEdge(u, w) < dist[w]) )
{
dist[w] = dist[u] + getEdge(u, w);
path[w] = u;
}
}
} LinkStack<int> s; s.push(j); for(int k=path[j]; k != -; k=path[k])
{
s.push(k);
} while( s.size() > )
{
ret.add(s.top()); s.pop();
}
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Index<i, j> is invalid...");
} if( ret.length() < )
{
THROW_EXCEPTION(ArithmeticException, "There is no path from i to j...");
} return toArray(ret);
} SharedPointer<Array<int>> floyd(int x, int y, const E& LIMIT)
{
LinkQueue<int> ret; if( ( <= x) && (x < vCount()) && ( <= y) && ( y < vCount()) )
{
DynamicArray< DynamicArray<E> > dist(vCount());
DynamicArray< DynamicArray<int> > path(vCount()); for(int k=; k<vCount(); k++)
{
dist[k].resize(vCount());
path[k].resize(vCount());
} for(int i = ; i<vCount(); i++)
{
for(int j=; j<vCount(); j++)
{
path[i][j] = -;
dist[i][j] = isAdjacent(i, j) ? (path[i][j]=j, getEdge(i, j)) : LIMIT;
}
} for(int k=; k<vCount(); k++)
{
for(int i = ; i<vCount(); i++)
{
for(int j=; j<vCount(); j++)
{
if( (dist[i][k] + dist[k][j]) < dist[i][j] )
{
dist[i][j] = dist[i][k] + dist[k][j];
path[i][j] = path[i][k];
}
}
}
} while( (x != -) && (x != y) )
{
ret.add(x);
x = path[x][y];
} if( x != - )
{
ret.add(x);
}
}
else
{
THROW_EXCEPTION(ArithmeticException, "Index<x, y> is invalid...");
} if( ret.length() < )
{
THROW_EXCEPTION(ArithmeticException, "There is no path from x to y...");
} return toArray(ret);
}
}; } #endif // GRAPH_H
测试程序如下:
#include <iostream>
#include "MatrixGraph.h"
#include "ListGraph.h" using namespace std;
using namespace DTLib; template< typename V, typename E >
Graph<V, E>& GraphEasy()
{
static MatrixGraph<, V, E> g; g.setEdge(, , );
g.setEdge(, , );
g.setEdge(, , );
g.setEdge(, , );
g.setEdge(, , ); return g;
} template< typename V, typename E >
Graph<V, E>& GraphComplex()
{
static ListGraph<V, E> g(); g.setEdge(, , );
g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , ); g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); return g;
} template< typename V, typename E >
Graph<V, E>& GraphSample()
{
static ListGraph<V, E> g(); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , ); return g;
} int main()
{
Graph<int, int>& g = GraphSample<int, int>();
SharedPointer<Array<int>> r = g.floyd(, , ); for(int i=; i<r->length();i++)
{
cout << (*r)[i] << " ";
} cout << endl;
return ;
}
结果如下:
小结:

第七十九课 最短路径(Floyd)的更多相关文章
- 第七十八课 最短路径(Dijkstra)
核心思想是从已知的最短路径推算未知的最短路径. 添加程序: #ifndef GRAPH_H #define GRAPH_H #include "Object.h" #include ...
- KALI LINUX WEB 渗透测试视频教程—第十九课-METASPLOIT基础
原文链接:Kali Linux Web渗透测试视频教程—第十九课-metasploit基础 文/玄魂 目录 Kali Linux Web 渗透测试视频教程—第十九课-metasploit基础..... ...
- NeHe OpenGL教程 第三十九课:物理模拟
转自[翻译]NeHe OpenGL 教程 前言 声明,此 NeHe OpenGL教程系列文章由51博客yarin翻译(2010-08-19),本博客为转载并稍加整理与修改.对NeHe的OpenGL管线 ...
- NeHe OpenGL教程 第二十九课:Blt函数
转自[翻译]NeHe OpenGL 教程 前言 声明,此 NeHe OpenGL教程系列文章由51博客yarin翻译(2010-08-19),本博客为转载并稍加整理与修改.对NeHe的OpenGL管线 ...
- NeHe OpenGL教程 第十九课:粒子系统
转自[翻译]NeHe OpenGL 教程 前言 声明,此 NeHe OpenGL教程系列文章由51博客yarin翻译(2010-08-19),本博客为转载并稍加整理与修改.对NeHe的OpenGL管线 ...
- python第二十九课——文件读写(复制文件)
自定义函数:实现文件复制操作有形参(2个) 没有返回值相似版(不用) def copyFile(src,dest): #1.打开两个文件:1个关联读操作,1个关联写操作 fr=open(src,'rb ...
- python第二十九课——文件读写(读取读取中文字符)
演示:读取中文字符 结论: 1).如果不设置encoding,默认使用gbk进行编解码 2).如果编码和解码不一致,最终导致报错,但是一旦设置了errors='ingore',那么就不会报错,而采取乱 ...
- 第三百七十九节,Django+Xadmin打造上线标准的在线教育平台—xadmin的安装
第三百七十九节,Django+Xadmin打造上线标准的在线教育平台—xadmin的安装 xadmin介绍 xadmin是基于Django的admin开发的更完善的后台管理系统,页面基于Bootstr ...
- “全栈2019”Java第七十九章:类中可以嵌套接口吗?
难度 初级 学习时间 10分钟 适合人群 零基础 开发语言 Java 开发环境 JDK v11 IntelliJ IDEA v2018.3 文章原文链接 "全栈2019"Java第 ...
随机推荐
- Linux mail 邮件发送
Linux mail 邮件介绍 在Linux系统下我们可以通过”mail“命令,发送邮件,在运维中通常我们它来实现邮件告警. 安装 (方案1) 一.安装邮件服务 yum install -y send ...
- (转) Ensemble Methods for Deep Learning Neural Networks to Reduce Variance and Improve Performance
Ensemble Methods for Deep Learning Neural Networks to Reduce Variance and Improve Performance 2018-1 ...
- java程序员面试交流项目经验
粘贴自:https://blog.csdn.net/wangyuxuan_java/article/details/8778211 1:请你介绍一下你自己 这是面试官常问的问题.一般人回答这个问题过于 ...
- Learning-Python【6】:Python数据类型(2)—— 列表、元组
一.列表类型 1.用途:记录多值,比如人的多个爱好 2.定义方式:在[ ]内用逗号分隔开多个任意类型的值 li = [1, 2, 3] 3.常用操作+内置方法 优先掌握的操作: 1)按索引存取值:可以 ...
- ASP.NET图片上传(配合jquery.from.js 插件)
前端: js: function AjaxKouBeiShopEdit() { var options = { dataType: "json&q ...
- Java项目中使用log记录日志的一些总结
本文介绍了一下自己在Java项目中使用log的一些总结,从日志的作用.日志的选用.日志级别介绍.日志记录的一些最佳实践几个方面阐述. 日志的作用 主要作用包括: 1.出问题后定位当时问题 2.显示程序 ...
- adt安装----只为测试使用adb命令,故无需安装过于复杂
下载并安装Android SDK 借鉴自原文 https://blog.csdn.net/qq_15304853/article/details/79168248 官网(可FQ选择):http:// ...
- 第 8 章 容器网络 - 068 - 分析 Calico 的网络结构
分析 Calico 的网络结构 在 host1 中运行容器 bbox1 并连接到 cal_net1: docker container run --network cal_net1 --name bb ...
- https 适配
1info plist <key>NSAppTransportSecurity</key> <dict> <key>NSAllowsArbitraryL ...
- rocketmq ----> 学习笔记
官网:http://rocketmq.apache.org 1.环境搭建 准备: rocketmq-all-4.3.0-bin-release.zip 必须配置:JAVA_HOME=/home/rui ...
