PAT A1127 ZigZagging on a Tree （30 分）——二叉树，建树，层序遍历

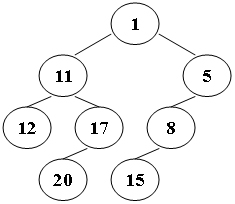
Suppose that all the keys in a binary tree are distinct positive integers. A unique binary tree can be determined by a given pair of postorder and inorder traversal sequences. And it is a simple standard routine to print the numbers in level-order. However, if you think the problem is too simple, then you are too naive. This time you are supposed to print the numbers in "zigzagging order" -- that is, starting from the root, print the numbers level-by-level, alternating between left to right and right to left. For example, for the following tree you must output: 1 11 5 8 17 12 20 15.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the inorder sequence and the third line gives the postorder sequence. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the zigzagging sequence of the tree in a line. All the numbers in a line must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

8
12 11 20 17 1 15 8 5
12 20 17 11 15 8 5 1

Sample Output:

1 11 5 8 17 12 20 15

 #include <stdio.h>
 #include <algorithm>
 #include <queue>
 using namespace std;
 const int maxn=;
 int pos[maxn],in[maxn];
 int n,m;
 vector<int> res[];
 struct node{
     int data;
     node* left,*right;
     int lvl;
 };
 node* create(int inl,int inr,int posl,int posr){
     if(inl > inr) return NULL;
     node* root = new node;
     root->data = pos[posr];
     int k;
     for(k=inl;k<=inr;k++){
         if(pos[posr]==in[k]) break;
     }
     int numleft=k-inl;
     root->left = create(inl,k-,posl,posl+numleft-);
     root->right = create(k+,inr,posl+numleft,posr-);
     return root;
 }
 void pr(node* root){
     queue<node*> q;
     root->lvl=;
     q.push(root);
     while(!q.empty()){
         node* now=q.front();
         q.pop();
         res[now->lvl].push_back(now->data);
         if(now->left!=NULL){
             now->left->lvl=now->lvl+;
             q.push(now->left);
         }
         if(now->right!=NULL){
             now->right->lvl=now->lvl+;
             q.push(now->right);
         }
     }
 }
 int main(){
     scanf("%d",&n);
     for(int i=;i<n;i++){
         scanf("%d",&in[i]);
     }
     for(int i=;i<n;i++){
         scanf("%d",&pos[i]);
     }
     node* root = create(,n-,,n-);
     pr(root);
     int cnt=;
     for(int i=;i<;i++){
         if(i%==){
             for(int j=res[i].size()-;j>=;j--){
                 printf("%d",res[i][j]);
                 cnt++;
                 if(cnt<n)printf(" ");
             }
         }
         else{
             for(int j=;j<res[i].size();j++){
                 printf("%d",res[i][j]);
                 cnt++;
                 if(cnt<n)printf(" ");
             }
         }
         if(cnt==n)break;
     }
 }

注意点：最简单的一道30分题了。只要会建树，再层序遍历，把每层的数据保存起来，再根据层数正着输出或是反向输出就ac了。

ps:也可以用deque双向队列更方便的实现。每层的输出其实可以不用开vector数组，一层遍历完后输出就好了。