关联规则挖掘算法之Apriori算法

Apriori算法是一种挖掘关联规则的频繁项集算法，其核心思想是通过候选集生成和情节的向下封闭检测两个阶段来挖掘频繁项集。

关于这个算法有一个非常有名的故事："尿布和啤酒"。故事是这样的：美国的妇女们经常会嘱咐她们的丈夫下班后为孩子买尿布，而丈夫在买完尿布后又要顺 手买回自己爱喝的啤酒，因此啤酒和尿布在一起被购买的机会很多。这个举措使尿布和啤酒的销量双双增加，并一直为众商家所津津乐道。

关联规则应用：

1. Apriori算法应用广泛，可用于消费市场价格分析，猜测顾客的消费习惯，比如较有名的“尿布和啤酒”的故事；

2.网络安全领域中的入侵检测技术；

3.可用在用于高校管理中，根据挖掘规则可以有效地辅助学校管理部门有针对性的开展贫困助学工作；

4.也可用在移动通信领域中，指导运营商的业务运营和辅助业务提供商的决策制定。

关联规则算法的主要应用是购物篮分析，是为了从大量的订单中发现商品潜在的关联。其中常用的一个算法叫Apriori先验算法。

项集：在关联分析中，包含0个或多个项的集合被称为项集（itemset）。如果一个项集包含k个项，则称它为k-项集。例如:{啤酒，尿布，牛奶，花生} 是一个4-项集。空集是指不包含任何项的项集。

关联规则（association rule）：是形如 X → Y 的蕴含表达式，其中X和Y是不相交的项集，即：X∩Y=∅。关联规则的强度可以用它的支持度（support）和置信度（confidence）来度量。

支持度：一个项集或者规则在所有事物中出现的频率，确定规则可以用于给定数据集的频繁程度。σ(X):表示项集X的支持度计数

项集X的支持度：s(X)=σ(X)/N；规则X → Y的支持度：s(X → Y) = σ(X∪Y) / N

通俗解释：简单地说，X==>Y的支持度就是指物品集X和物品集Y同时出现的概率。

概率描述：物品集X对物品集Y的支持度support（X==>Y）=P（X n Y）

实例说明：某天共有1000 个顾客到商场购买物品，其中有150个顾客同时购买了圆珠笔和笔记本，那么上述的关联规则的支持度就是15％。

置信度：确定Y在包含X的事务中出现的频繁程度。c(X → Y) = σ(X∪Y)/σ(X)

通俗解释：简单地说，可信度就是指在出现了物品集X 的事务T 中，物品集Y 也同时出现的概率有多大。

概率描述：物品集X对物品集Y的置信度confidence（X==>Y）=P（X|Y）

实例说明：上该关联规则的可信度就回答了这样一个问题：如果一个顾客购买了圆珠笔，那么他也购买笔记本的可能性有多大呢？在上述例子中，购买圆珠笔的顾客中有65％的人购买了笔记本, 所以可信度是65％。

期望置信度（Expected confidence）

定义：设W 中有e ％的事务支持物品集B，e ％称为关联规则A→B 的期望可信度度。

通俗解释：期望可信度描述了在没有任何条件影响时，物品集B 在所有事务中出现的概率有多大。

实例说明：如果某天共有1000 个顾客到商场购买物品，其中有250 个顾客购买了圆珠笔，则上述的关联规则的期望可信度就是25 ％。

概率描述：物品集A对物品集B的期望置信度为support（B）=P（B）

提升度（lift）

定义：提升度是可信度与期望可信度的比值

通俗解释：提升度反映了“物品集A的出现”对物品集B的出现概率发生了多大的变化。

实例说明：上述的关联规则的提升度=65%/25%=2.6

概率描述：物品集A对物品集B的期望置信度为lift（A==>B）=confidence（A==>B）/support(B)=p(B|A)/p(B)

支持度是一种重要的度量，因为支持度很低的规则可能只是偶然出现，低支持度的规则多半也是无意义的。因此，

支持度通常用来删去那些无意义的规则；

置信度度量是通过规则进行推理具有可靠性。对于给定的规则X → Y，置信度越高，Y在包含X的事物中出现的可能性就越大。即Y在给定X下的条件概率P(Y|X)越大。

一句话关联规则：关联规则是展现项集(itemsets)间关联(association)与相关性(correlation)的规则！

如何来度量一个规则是否够好？

有两个量，置信度(Confidence)和支持度(Support)。

支持度：就是概率（一项就是其出现的概率，多项就是其同时出现的概率）

置信度：条件概率（A出现后，B也出现的概率）

总之，可信度是对关联规则的准确度的衡量，支持度是对关联规则重要性的衡量。支持度说明了这条规则在所有事务中有多大的代表性，显然支持度越大，关联规则越重要。有些关联规则可信度虽然很高，但支持度却很低，说明该关联规则实用的机会很小，因此也不重要。

在关联规则挖掘中，满足一定最小置信度以及支持度的集合成为频繁集（frequent itemset），或者强关联。关联规则挖掘则是一个寻找频繁集的过程。

几个重要公式：

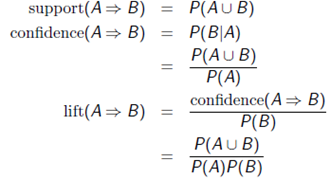
P(A)是包含A项的case(这里的cases即为数据库中的transaction每笔交易记录)百分比或概率！

使用Aprior算法挖掘频繁项集，关联规则或者关联超边(hyperedge)，Aprior算法运用逐层(level-wise)方法搜索频繁项集。

#####用法说明

apriori(data, parameter = NULL, appearance = NULL, control = NULL)

#####参数说明

Data：交易数据(transactions)类对象或任何能够被转化成transaction的数据结构

Parameter：APparameter类对象或命名列表。挖掘规则默认的行为是：支持度=0.1；置信度=0.8；输出的最大规则长度；

Appearance：APappearance类对象或命名列表。

Control：APcontrol类对象或命名列表。控制挖掘算法的性能！

####细节说明

APparameter中minlen(最小规则数)默认的值是1，这意味着将会产生只有一项(item:比如,先前项/LHS)的规则：{}=>{beer}—这项规则说明，no matter what other items are involved the item in the RHS will appear with the probability given by the rule's confidence (which equals the support)。如果想要避免这些规则，可以使用参数：parameter=list(minlen=2)！

####返回值说明：返回一个rules类对象或itemsets类对象。

实例：

library(arules) #载入arules包
library(grid)
library(arulesViz)  # 加载可视化包
data("SunBai") #一个小例子数据库作为类的一个对象提供的加权关联规则挖掘
summary(SunBai) #summary的结果和具体含义如##中所示
#探索和准备数据：
#（1）事务型数据每一行指定一个单一的实例，每条记录包括用逗号隔开的任意数量的产品清单
# 通过inspect()函数可以看到超市的交易记录，每次交易的商品名称；
# 通过summary()函数可以查看该数据集的一些基本信息。
#总共有6条交易记录transaction，8个商品item。density=0.375表示在稀疏矩阵中1的百分比。最频繁出现的商品item，以及其出现的次数。可以计算出最大支持度。
# 每笔交易包含的商品数目，以及其对应的5个分位数和均值的统计信息。如：一条交易包含一件商品；一条包含两件；两条包含三件；一条包含四件；一条包含五件。其下统计信息表明：最低一次交易只含一件商品，第一分位数是2.25，意味着25%的交易包含不超过2.25个item。中位数是3表面50%的交易购买的商品不超过3件。

<注> lhs=left hand side；rhs=right hand side.

2）关联规则—调整参数

#如果只想检查其它变量和客户是否幸存的关系，那么需要提前设置变量rhs=c("Survived=No", "Survived=Yes")

inspect(SunBai[1:5]) #通过inspect函数查看SunBai数据集的前5次交易记录

itemFrequency(SunBai[,1:3]) #itemFrequency()函数可以查看商品的交易比例

itemFrequencyPlot(SunBai,support = 0.1) # support = 0.1 表示支持度至少为0.1
itemFrequencyPlot(SunBai,topN = 20) # topN = 20 表示支持度排在前20的商品
head(transactionInfo(SunBai))  利用transactionInfo函数查看前六数据

# 训练模型
rules=apriori(SunBai,parameter = list(support=0.2,confidence=0.5))#设置支持度0.2，置信度0.5对数据进行关联规则处理
# rules=apriori(SunBai,parameter = list(support=0.2,confidence=0.5,minlen = 2)) #minlen = 2 表示规则中至少包含两种商品，这可以防止仅仅是由于某种商品被频繁购买而创建的无用规则
summary(rules)

#提高模型的性能
# 根据购物篮分析的目标，最有用的规则或许是那些具有高支持度、信度和提升度的规则。arules包中包含一个sort()函数，通过指定参数by为"support","confidence"或者"lift"对规则列表进行重新排序。 在默认的情况下，排序是降序排列，可以指定参数decreasing=FALSE反转排序方式。

inspect(head(sort(rules, by = "lift"), 3))#lift（提升度），表示用来度量一类商品相对于它的一般购买率，此时被购买的可能性有多大 (Lift)是避免了一些不平衡数据标签的偏差性，Lift越大，则数据质量较好；Lift越小，则数据越不平衡。在此处设置lift值为3.

library(arulesViz) # 加载可视化包

plot(rules, method = "grouped")

plot(rules, method='scatterplot') # 散点图判断大量规则的支持度与置信度分布情况

plot(rules,interactive=TRUE) #可以使用interactive=TRUE来实现散点图的互动功能，可以选中一些点查看其具体的规则

还有类似“气泡图”的展现形式：提升度lift是圈的颜色深浅，圈的大小表示支持度support的大小。LHS的个数和分组中最重要（频繁）项集显示在列的标签里。lift从左上角到右下角逐渐减少。

plot(rules, method='graph', shading = "lift",  control = list(type='items'))  # 关联图看相互关系

# measure 定义圆圈大小，shading 控制颜色深浅

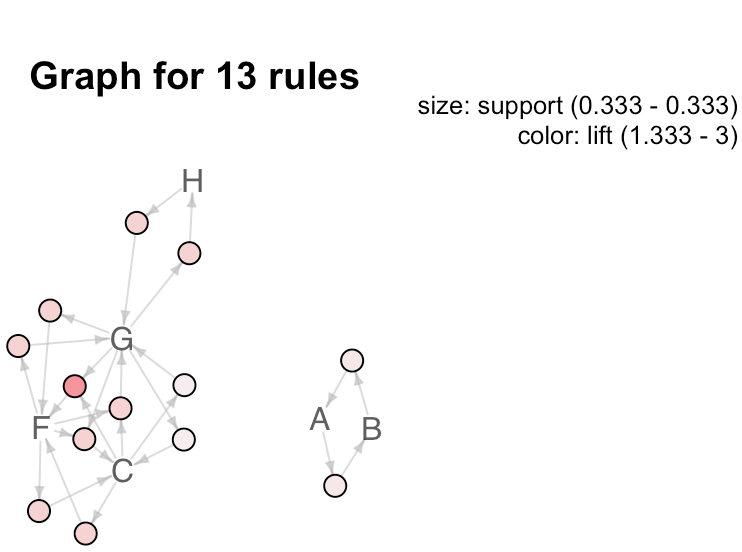
通过箭头和圆圈来表示关联规则，利用顶点代表项集，边表示规则中关系。圆圈越大表示支持度support越大，颜色越深表示提升度lift越大。但是如果规则较多的话会显得很混乱，难以发现其中的规律，因此，通常只对较少的规则使用这样的图;

# 提取关联规则的子集：可以通过subset()函数提取我们感兴趣的规则

sub_rules<-subset(rules,items %in% "C");sub_rules
inspect(sub_rules[1:5])

插播—函数介绍：

Is.subset(x,y=NULL, proper=FALSE, sparse=FALSE,...) #is.subset和is.superset函数用于在关联和项集矩阵对象中发现子集或父集！

Lower.tri(x,diag=FALSE) #返回一个与给定矩阵(在上三角或下三角中TRUE)相同大小的逻辑矩阵

提升度(lift)

Lift(A->B) = Confidence(A->B)/Support(B) 即A出现后，B也出现的条件概率除以B出现的概率。

为什么需要提升度呢？

比如：100条购买记录中，有60条包含牛奶，75条包含面包，其中有40条两者都包含。关联规则（牛奶，面包）的支持度为0.4，看似很高，但其实这个关联规则是一个误导。在用户购买了牛奶的前提下，有(40/60 = ) 0.67的概率去购买面包，而在没有任何前提条件时，用户反而有(75/100 = ) 0.75的概率去购买面包。也就是说，设置了购买牛奶的前提会降低用户购买面包的概率，也就是说面包和牛奶是互斥的。

如果lift=1，说明两个事项没有任何关联；如果lift<1，说明A事件的发生与B事件是相斥的。一般在数据挖掘中当提升度大于3时，我们才承认挖掘出的关联规则是有价值的。

参考来源于：http://www.cnblogs.com/dm-cc/p/5737147.html　　

　　　　　　http://sanwen.net/a/kezpeoo.html

　　　　　　http://www.cdadata.com/14444