单片机成长之路(51基础篇) - 008 C51 的标示符和关键字
标准 C 语言定义了 32 个关键字,如下表(ANSI C的32个关键字):
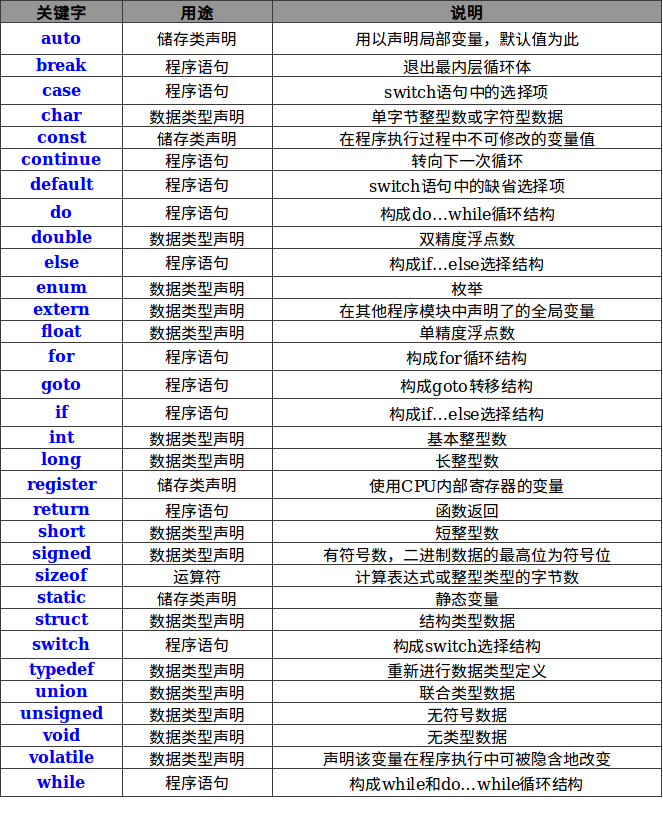
C51在此基础上针对单片机功能进行了扩展,详情见下表(C51编译器扩充关键字):
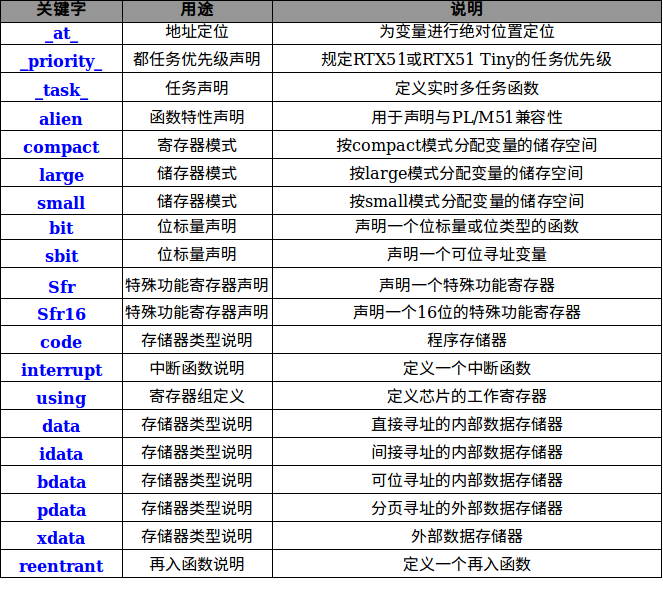
C 51的数据类型
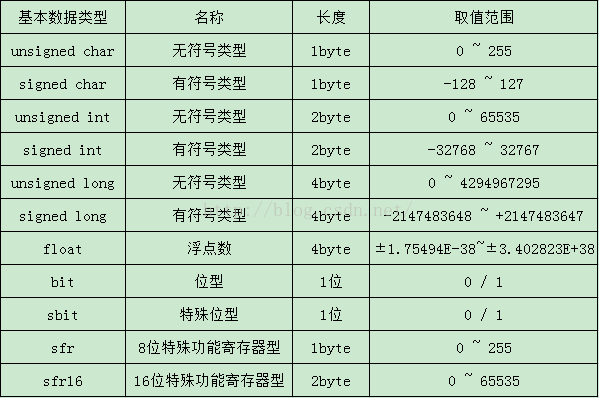
51单片机使用的C语言的存储器类型分为以下几种:
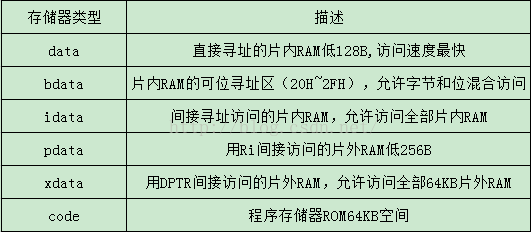
单片机成长之路(51基础篇) - 008 C51 的标示符和关键字的更多相关文章
- 单片机成长之路(51基础篇) - 015 关于sdcc的多文件编译范例二
本文是续 单片机成长之路(51基础篇) - 009 关于sdcc的多文件编译范例(一)编写的. 在实际的工作中,单片机的头文件和功能函数不可能同全部放在同一个文件夹下面,我们把单片机成长之路(51基础 ...
- 单片机成长之路(51基础篇) - 009 关于sdcc的多文件编译范例(一)
本文是续 单片机成长之路(51基础篇) - 006 在Linux下搭建51单片机的开发烧写环境编写的. 本范例主要由(main.c ,delay.h,delay.c,makefile)4个文件组成,s ...
- (转)Python成长之路【第九篇】:Python基础之面向对象
一.三大编程范式 正本清源一:有人说,函数式编程就是用函数编程-->错误1 编程范式即编程的方法论,标识一种编程风格 大家学习了基本的Python语法后,大家就可以写Python代码了,然后每个 ...
- Sass进阶之路,之一(基础篇)
Sass 学习Sass之前,应该要知道css预处理器这个东西,css预处理器是什么呢? Css预处理器定义了一种新的语言将Css作为目标生成文件,然后开发者就只要使用这种语言进行编码工作了.预处理器通 ...
- python成长之路第三篇(1)_初识函数
目录: 函数 为什么要使用函数 什么是函数 函数的返回值 文档化函数 函数传参数 文件操作(二) 1.文件操作的步骤 2.文件的内置方法 函数: 一.为什么要使用函数 在日常写代码中,我们会发现有很多 ...
- C++自学成长之路(第一篇)
今天开始我将开启C++自学成长之路,今天是第一天,在以前就一直在网上查找关于c++的资料,想买一本好一点的,权威一点的资料书,通过努力查找,我选择了c++ primer,在网上这本书的好评如潮.更多的 ...
- 单片机成长之路(51基础篇) - 006 在Linux下搭建51单片机的开发烧写环境
在Linux下没有像keli那样好用的IDE来开发51单片机,开发环境只能自己搭建了. 第一步:安装交叉编译工具 a) 安装SDCC sudo apt-get install sdcc b)测试SDC ...
- 单片机成长之路(51基础篇) - 002 STC单片机冷启动和复位有什么区别
STC单片机简介 STC单片机是一款增强型51单片机,完全兼容MCS-51,还增加了新的功能,比如新增两级中断优先级,多一个外中断,内置EEPROM,硬件看门狗,具有掉电模式,512B内存等.还支持I ...
- 单片机成长之路(51基础篇) - 017 C51中data,idata,xdata,pdata的区别(转)
从数据存储类型来说,8051系列有片内.片外程序存储器,片内.片外数据存储器,片内程序存储器还分直接寻址区和间接寻址类型,分别对应code.data.xdata.idata以及根据51系列特点而设定的 ...
随机推荐
- Qt Creator插件Todo
转载:http://techieliang.com/2017/12/502/ 文章目录 1. 插件启动 2. 插件效果 3. 插件配置 4. 使用 码代码的过程往往并不是一气呵成,有时候需要记录 ...
- ZOJ 1109 Language of FatMouse 【Trie树】
<题目链接> 题目大意: 刚开始每行输入两个单词,第二个单词存入单词库,并且每行第二个单词映射着对应的第一个单词.然后每行输入一个单词,如果单词库中有相同的单词,则输出它对应的那个单词,否 ...
- kafka-manager配置和使用
kafka-manager配置 最主要配置就是用于kafka管理器状态的zookeeper主机.这可以在conf目录中的application.conf文件中找到. kafka-manager.zkh ...
- AS安装过程中出现的错误
1.首先是You may need to adjust the proxy settings in Gradle.的错误, 主要是看你有没有图中红线所画的gradle的压缩包 如果没有,那就前往htt ...
- 大数据环境完全分布式搭建 hadoop2.4.1
(如果想要安装视频及相关软件可以博私聊我 qq 731487514) hadoop2.0已经发布了稳定版本了,增加了很多特性,比如HDFS HA.YARN等.最新的hadoop-2.4.1又增加了YA ...
- 潭州课堂25班:Ph201805201 django框架 第五课 自定义简单标签,包含标签,模型类创建,梳理类创建 (课堂笔记)
自定义标签同自定义过渡器一样,要创建文件,在配置文件中以APP方法注册,对方法进注册,在 html 文件中引入,.. 由模板传参 在 在配置文件中改时区: 由视图函数传参 包含标签: 当有这种重复的代 ...
- [CF536D]Tavas in Kansas
[CF536D]Tavas in Kansas 题目大意: 一张\(n(n\le2000)\)个点,\(m(m\le10^5)\)条边的无向带权连通图(权值可以为负).A.B两人分别在\(s,t\)点 ...
- Unable to find utility "instruments", not a developer tool or in PATH
在调试ios上的项目的时候出现报错 unable to find utility "instruments", not a developer tool or in PATH 报错 ...
- BZOJ2647 : [Neerc2011]Journey
$|x|+|y|=\max(x+y,x-y,-x+y,-x-y)$,设$f[i][j]$表示在$(0,0)$,朝向方向$j$,执行第$i$条指令后的信息: $cir$:是否陷入循环 $d$:朝向 $x ...
- BZOJ2616 : SPOJ PERIODNI
长为$A$,宽为$B$的矩阵放$K$个车的方案数$=C(A,K)\times C(B,K)\times K!$. 建立笛卡尔树,那么左右儿子独立,设$f[i][j]$表示$i$子树内放$j$个车的方案 ...
