BUAAOO第一单元的总结

---恢复内容开始---

Homework1 简单多项式求导

程序架构

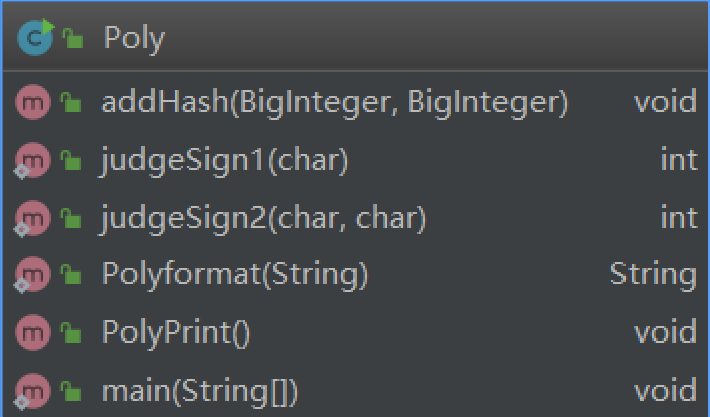
由于对java的生疏和不了解，第一次作业很羞愧的只用了一个类。

1.在输入之后调用Polyformat函数检查输入的格式，A检索有无非法字符，B检索有符号整数格式，C消除所有空格并对表达式前加符号。

2.调用Poly构造器，使用正则表达式对表达式进行处理，将得到的一个个因子的导数调用addhash存入hashmap中，并在检索完成之后再对所得到的字符串的长度求和并与传入Poly的表达式长度比较来完成最后一次格式检查。

3调用PolyPrint将hashmap中的表达式整理化简并且输出。

BUG的出现

1.输入对\S和与\t的混淆。

        for (int i = 0; i < str.length(); i++) {

            if (!str.substring(i, i + 1).matches("[\\d\\sx*^\\+\\-]")) {

                return "WRONG FORMAT!";

            }

        }

如上代码就会导致对本应该判定WF的\f输入却判定为正常输入。

应该修改为如下代码：

if (!str.substring(i, i + 1).matches("[\\d\\t x*^\\+\\-]")) {

                return "WRONG FORMAT!";

            }

2.对当输入为空串或者是hashmap为空时无任何输出。这个修改也较为简单在此不多赘述。

Homework2 包含简单幂函数和简单正余弦函数的导函数

程序架构

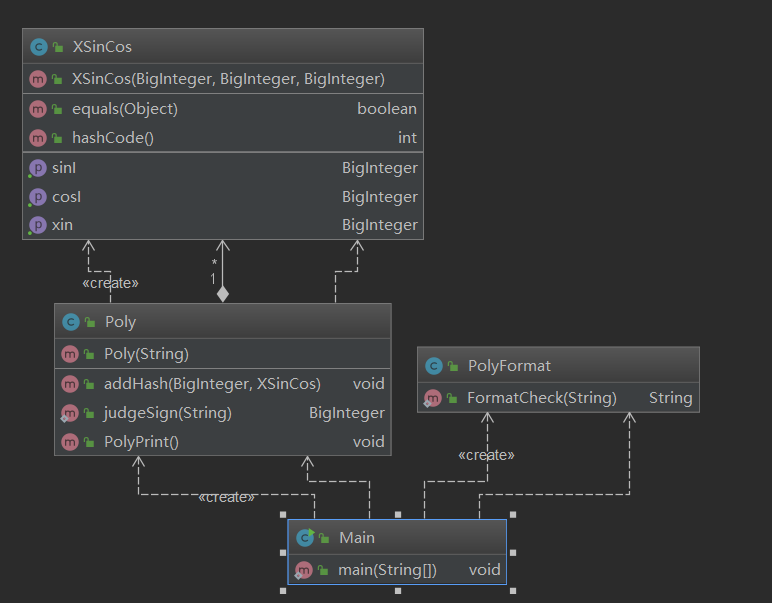
第二次作业对第一次作业的复用非常多。

1.PolyFormat类只是从之前的Poly类分出来用于美观，其中检查方法几乎不变，只是对sin(x)cos(x)等字符的引入和对+++等几个小细节的检查增加罢了。

2.在Poly类的构建之中，思路仍然一样，即将项一个一个分出来，然而对项的处理我是直接统计x的次数，sin(x)的次数和cos(x)的次数和系数，分成这四个部分，再直接应用乘法求导法则，将这个项的求导分成三个导数生成，再将这三个导数录入hashmap，当然hashmap也有所变动，它的key化为了XSinCos类，而value仍然是系数，然后在存入时完成合并同类项工作。

3最后在PolyPrint中输出。

BUG的出现

说起来也冤，我的一个化简bug被强测de了5个，直接导致强测爆炸。直接上错误代码

            for (int i = 0; i < ss.length() - 1; i++) {

                if (ss.charAt(i) == '1' && ss.charAt(i + 1) == '*') {

                    ss.delete(i, i + 2);

                }

            }

我做出了极其愚蠢的优化，原本我是为了化简一个项前多出的1*，然而一旦进行上述的代码操作就会使所有包含1*的式子都被消去，例如21*x会被化简为2x，例如x*sin(x)^1*cos(x)会被化简为x*sin(x)^cos(x)。

Homework3 包含简单幂函数和简单正余弦函数的导函数

程序架构

在第三次作业，我完全推翻了前两次作业的架构，因为有了嵌套，我无法仅仅通过简单的正则表达式从一串表达式中提取我所需要计算的项，因此前两次的架构是完全无法适用第三次作业的。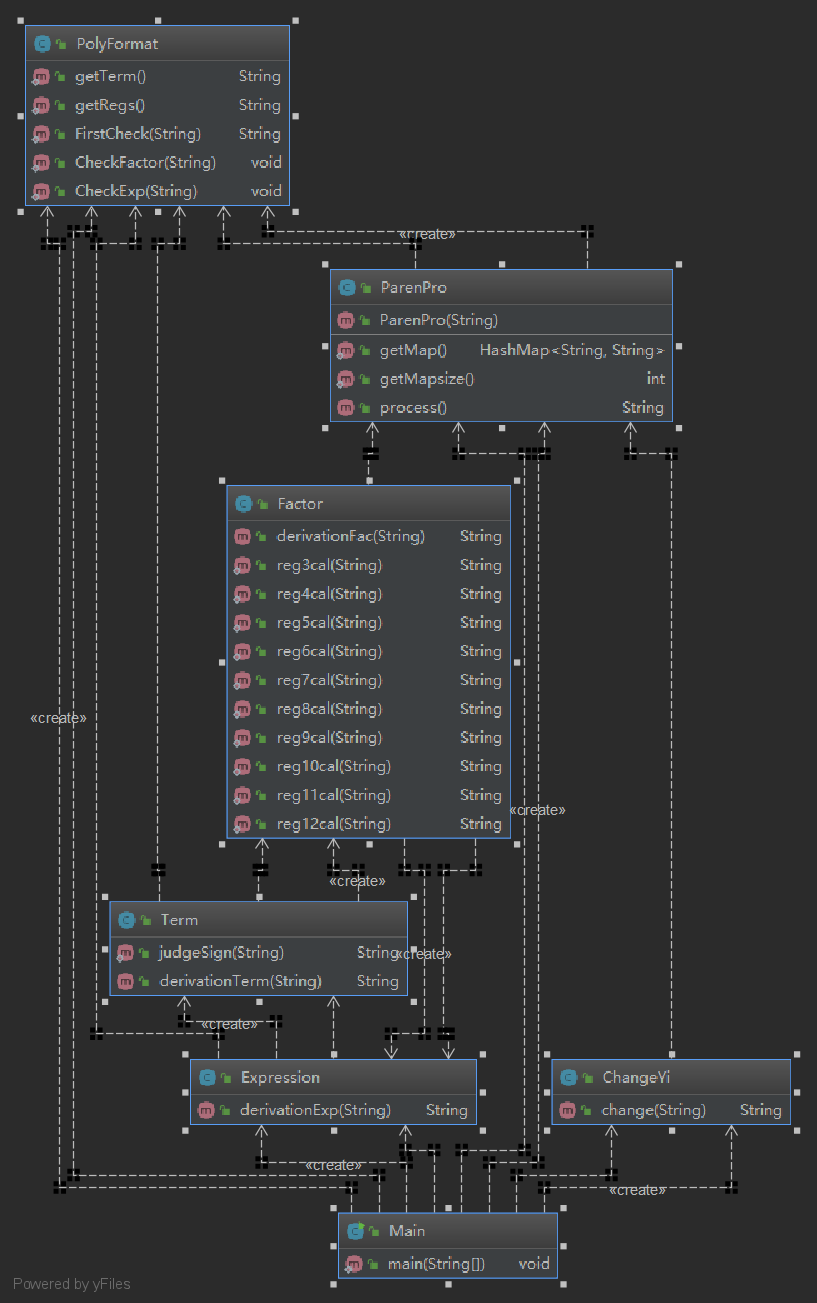

1.使用PolyFormat的FirstCheck()进行如第一二次作业的最基础的检查，这个检查非常基础，仅仅是初次的排除很明显的格式错误。

2.用ParenPro对表达式进行切分处理。具体细节：使用栈从内向外对括号进行检查，从最内层的括号开始提取括号中的式子并且将它替换为y1，y2，y3……例如3*sin(cos(x))*(1+3*x)会被替换为3*sin(y2)*(y3),而y2为cos(y1),y3为(1+3*x)，y1为x，注意替换的差异：sincos(x)和（表达式）不同，因为还需要对yi进行format检查，而sincos()内仅仅只能是因子，而（表达式）里可以是表达式也可以是因子（*单一因子也是表达式），所以替换有差异，而且(表达式)是要将括号也替换，而sincos只要将括号中的内容替换即可。替换的yi存入ParenPro的hashmap中，yi为key，yi代表的串为value，用于之后的递归调用。

3.在替换过程中，调用PolyFormat中的checkFactor()检查sincos的yi所表示的因子，用checkExp()检查（表达式）的yi所表示的表达式，内部即可用正则即可，因为在2.中是由内向外分解括号的，因此保证yi所表示的式子最多只有单层括号存在，即sin（）和cos（），当然还得注意因子的增加，yi因子和sincos(yi)^的增加，只要使用正则表达式即可完成检查工作。

4.完成替换工作，即可将替换完的字符串传入Expression类中进行求导，Expression对字符串进行分割，将分割的一个个项传入Term中进行运算，Term中继续分割项为因子，将因子传入Factor项中进行运算，Factor中完成递归调用，若为普通因子直接计算，若含有yi，从hashmap中调出yi的字符串再次传入Expression中进行运算，从而完成递归调用工作。

5.最后传出的求导字符串仍然含有yi，因此要最后一次调用change函数再次使用hashmap将yi依次替换，最后就为求出的式子。

复杂度分析

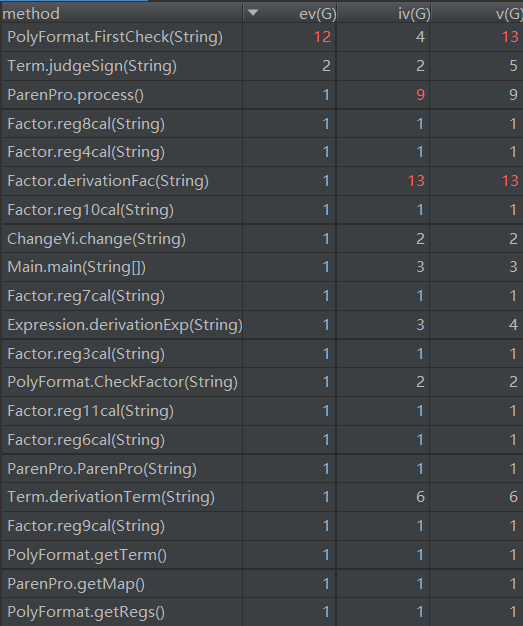
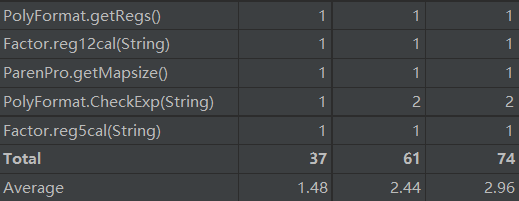
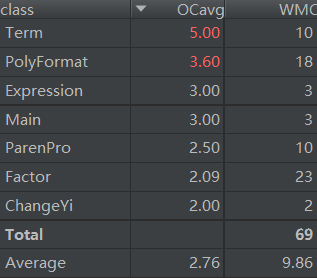
可以看出PolyFormat的FirstCheck函数的非结构化程度和结构复杂程度都十分高，这就是因为它调用众多正则表达式并进行多次单独的循环判断所造成。而Factor类的detivationFac的程序耦合度相当高，因为它是进行递归的环节，需要再次调用Expression类，并且我对每个因子都创建了一个求导方法，从而造成耦合度高、独立路径多。我感觉在这两块上还是有太多欠缺的地方了。

BUG的出现

第三次最主要的一个bug就是对sin(- 10)的输入无法判断为WF，其主要原因就是FirstCheck()的处理出现问题。由于对第二次代码的复用，没有考虑sincos()检查内部是否为因子的操作，在firstcheck中只会检查有符号整数是否正确，然后去空格，从而导致原本为表达式的- 10被化简为因子-10，从而产生bug。我思考了一下，直接在firstcheck中加入特判，因为sincos(- 10)的出现仅仅会出现在最内部的括号中，即第一次检查一定可以检查到，所以用正则特判就能解决这个问题。

三次作业总结

优点

没有使用长正则表达式，而是使用while(m.find){m.group()}的结构对表达式进行拆分判别，从而减少了爆栈的出现。

缺点

十分多

1：表达式化简极其偷懒。虽然第一二次都进行了化简，但是第三次作业几乎没有化简，造成大量多余括号和*1、*0的出现使表达式变得臃肿冗余。

2：对面向对象的理解十分浅薄。虽然第三次分成了Exp、Term、Factor类，但是类之间耦合关系仍然严重，面向过程化仍然严重。

3：程序的适用性很差。因为没有太多考虑架构问题，如果有所变动，可能需要大改。

4：鲁棒性很差。对于try-catch的使用太过于生疏（其实根本没有用），造成奇怪的输入就可能会使程序崩溃。

总结

总的来说，第一单元的作业算是java的入门，但是也非常的艰难，因为从无到有的过程本身就是最为艰难的。我还有许多欠缺的，对整个程序的架构，对继承接口等掌握，对try-catch的熟悉，还有对调试的熟练程度都是我应该重视并且赶紧练习的。我也没啥好的经验能和大家分享的，只有继续向大家学习。

---恢复内容结束---