浅谈线段树 Segment Tree

　　　众所周知，线段树是algo中很重要的一项！

　一.简介

　　　　

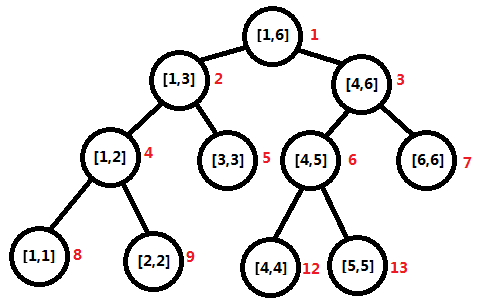
　　线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

　　使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。而未优化的空间复杂度为2N，实际应用时一般还要开4N的数组以免越界，因此有时需要离散化让空间压缩。

　　　二.用途

　　单点 ： 查询（query）修改（add,mul）

　　　　区间 ： 查询（区间和），修改，最大值（max)，最小值（min)。

　　

　　三. 实现方式

　　1.建树

　　　由于每个点都表示一个区间，所以他有很多信息（左儿子，右儿子，区间sum）　所以我们用结构体存. 因为之后要用到懒标记，所以结构体还有两个懒标记。

　　懒标记   ： 以上图为例，如果想在1 - 6区间内加一，我们就将这个信息从根节点传递到下一层，这时2,3点都有一个add = 1的懒标记，这样就表示已经加过1了，下次如果还要加，那么直接加在懒标记上。就比如你挣了一笔钱，暂时不用，就存在银行里了。之后如果求解需要递归，那么这个懒标记就向下传，并且传完后自己要清零！（这样更新后的状态就是 原状态 + 子区间点的个数 * 传下里的懒标记，（example  sum = 5(原状态）+ 4（区间里有4个数，都加了个2） * 2（懒标记））-------很玄学

　　乘法的懒标记（luogu p3373）：需要特别注意下

　　　　比如 懒标记原本为2 + 3
　　现在传下一个乘8 那么就变为（2 + 3) * 8
　　然后再传一个加三，就会变成（2 + 3 + 3） * 8
　　所以我们这么存 2 * 8 + 3 * 8
　　这样加3后值才是正确的！

　　上代码

代码中% P 为题目要求

 struct Node {
     int l, r;
     ll sum;
     ll add, mul;

     Node() {
         l = r = sum = add = ;
         mul = ;
     }

     void update_add(ll value) {
         add = (add + value) % P;
         sum = (sum + (r - l + ) * value) % P;
     }

     void update_mul(ll value) {
         sum = (sum * value) % P;
         mul = (mul * value) % P;
         add = (add * value) % P;
     }
 } t[N << ];

我的建树可能比较怪，当递归到根节点再cin，一边递归一边更新（push_up,后面有）

 void build_tree(int p, int l, int r) {
     t[p].l = l, t[p].r = r;
     if (l == r) {
         cin >> t[p].sum;
         return;
     }
     int mid = (t[p].l + t[p].r) >> ;
     build_tree(lc(p), l, mid);
     build_tree(rc(p), mid + , r);
     push_up(p);
 }

左儿子右儿子

inline int lc(int p) {
    return p << ;
}

inline int rc(int p) {
    return p <<  | ;
}

向上push_up更新信息（sum),向下传懒标记（push_down) 切记传完后自己状态要恢复哦！

 void push_up(int p) {
     t[p].sum = t[lc(p)].sum + t[rc(p)].sum;
 }

 void push_down(int p) {
     if (t[p].mul != ) {
         t[lc(p)].update_mul(t[p].mul);
         t[rc(p)].update_mul(t[p].mul);
         t[p].mul = ;
     }
     if (t[p].add) {
         t[lc(p)].update_add(t[p].add);
         t[rc(p)].update_add(t[p].add);
         t[p].add = ;
     }
 }

Å%%%Then

当我们进行区间改动时

（黑色为总区间，红色为需要修改的区间）

如果当前区间是全部区间的子集————那很好，咱们可以直接修改

如果当前区间和总区间有交集，那么就递归，找到第一个完全包含他的区间，然后修改，再递归上去

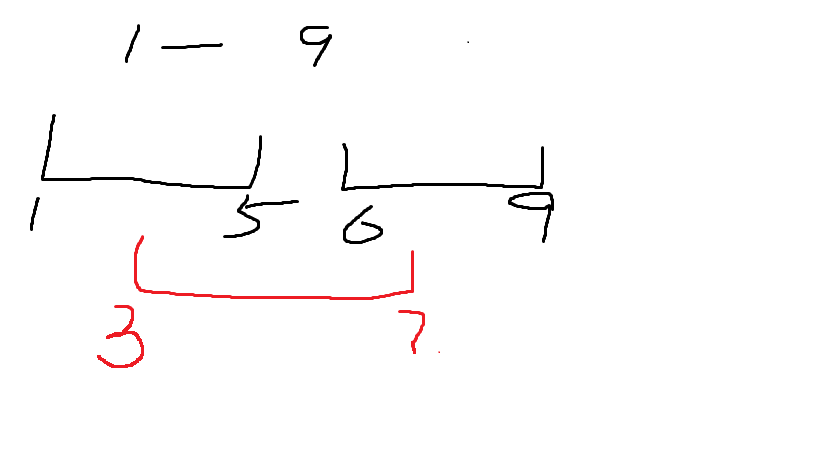
上代码！！！

 void update1(int p, int l, int r, ll value) {//乘法更新
     if (t[p].l >= l && t[p].r <= r) {
         t[p].update_mul(value);
         return;
     }
     push_down(p);
     int mid = (t[p].l + t[p].r) >> ;
     if (l <= mid) update1(lc(p), l, r, value);
     if (r > mid) update1(rc(p), l, r, value);
     push_up(p);
 }

 void update2(int p, int l, int r, ll value) {//加法更新
     if (t[p].l >= l && t[p].r <= r) {
         t[p].update_add(value);
         return;
     }
     push_down(p);
     int mid = (t[p].l + t[p].r) >> ;
     if (l <= mid) update2(lc(p), l, r, value);
     if (r > mid) update2(rc(p), l, r, value);
     push_up(p);
 }

 ll query(int p, int l, int r) {//区间查询，如果是单点差距的话l == r
     if (t[p].l >= l && t[p].r <= r) {
         return t[p].sum % P;
     }
     push_down(p);
     ll sum = ;
     int mid = (t[p].l + t[p].r) >> ;
     if (l <= mid) sum = (sum + query(lc(p), l, r)) % P;
     if (r > mid) sum = (sum + query(rc(p), l, r)) % P;
     return sum % P;
 }

当然还可以求RMQ问题

 struct Node
 {
     ll minn,maxx;
 }t[];

 //build 里加几句
 t[p].maxx = max(t[lc(p)].maxx,t[rp(p)].maxx);
 t[p].minn = min(t[lc(p)].minn,t[rp(p)].minn);

 int ans1,ans2;
 void new_query(int p,int l,int r)
 {
     if(t[p].l == l && t[p].r == r)
     {
         ans1 = max(ans1,t[p].maxx);
         ans2 = max(ans2,t[p].minn);
         return;
     }
     int mid = (t[p].l + t[p].r) >> ;
     if(r <= mid)
         query(lc(p),l,r);
     else if (l > mid)
         query(rc(p),l,r);
     else
     {
         query(lc(p),l,mid);
         query(rp(p),mid + ,r);
     }
 }

下面附上总代码（代码按照luogu 线段树2的模板打的，可AC）

 #include <iostream>
 #include<algorithm>
 using namespace std;
 const int N = 1e5 + ;
 typedef long long ll;

 ll P;

 struct Node {
     int l, r;
     ll sum;
     ll add, mul;
 //    ll minn,mmax;
     Node() {
         l = r = sum = add = ;
         mul = ;
     }

     void update_add(ll value) {
         add = (add + value) % P;
         sum = (sum + (r - l + ) * value) % P;
     }

     void update_mul(ll value) {
         sum = (sum * value) % P;
         mul = (mul * value) % P;
         add = (add * value) % P;
     }
 } t[N << ];

 inline int lc(int p) {
     return p << ;
 }

 inline int rc(int p) {
     return p <<  | ;
 }

 void push_up(int p) {
     t[p].sum = t[lc(p)].sum + t[rc(p)].sum;
 }

 void push_down(int p) {
     if (t[p].mul != ) {
         t[lc(p)].update_mul(t[p].mul);
         t[rc(p)].update_mul(t[p].mul);
         t[p].mul = ;
     }
     if (t[p].add) {
         t[lc(p)].update_add(t[p].add);
         t[rc(p)].update_add(t[p].add);
         t[p].add = ;
     }
 }

 void build_tree(int p, int l, int r) {
     t[p].l = l, t[p].r = r;
     if (l == r) {
         cin >> t[p].sum;
         return;
     }
     int mid = (t[p].l + t[p].r) >> ;
     build_tree(lc(p), l, mid);
     build_tree(rc(p), mid + , r);
 //    t[p].maxx = max(t[lc(p)].maxx,t[rp(p)].maxx);
 //    t[p].minn = min(t[lc(p)].minn,t[rp(p)].minn);
     push_up(p);
 }

 void update1(int p, int l, int r, ll value) {
     if (t[p].l >= l && t[p].r <= r) {
         t[p].update_mul(value);
         return;
     }
     push_down(p);
     int mid = (t[p].l + t[p].r) >> ;
     if (l <= mid) update1(lc(p), l, r, value);
     if (r > mid) update1(rc(p), l, r, value);
     push_up(p);
 }

 void update2(int p, int l, int r, ll value) {
     if (t[p].l >= l && t[p].r <= r) {
         t[p].update_add(value);
         return;
     }
     push_down(p);
     int mid = (t[p].l + t[p].r) >> ;
     if (l <= mid) update2(lc(p), l, r, value);
     if (r > mid) update2(rc(p), l, r, value);
     push_up(p);
 }

 ll query(int p, int l, int r) {
     if (t[p].l >= l && t[p].r <= r) {
         return t[p].sum % P;
     }
     push_down(p);
     ll sum = ;
     int mid = (t[p].l + t[p].r) >> ;
     if (l <= mid) sum = (sum + query(lc(p), l, r)) % P;
     if (r > mid) sum = (sum + query(rc(p), l, r)) % P;
     return sum % P;
 }
 /*int ans1,ans2;
 void new_query(int p,int l,int r)
 {
     if(t[p].l == l && t[p].r == r)
     {
         ans1 = max(ans1,t[p].maxx);
         ans2 = max(ans2,t[p].minn);
         return;
     }
     int mid = (t[p].l + t[p].r) >> 1;
     if(r <= mid)
         new_query(lc(p),l,r);
     else if (l > mid)
         new_query(rc(p),l,r);
     else
     {
         new_query(lc(p),l,mid);
         new_query(rp(p),mid + 1,r);
     }
 }
 */

 int main()
 {
     int n, m;
     cin >> n >> m >> P;
     build_tree(, , n);
     while (m--) {
         int op, l, r, num;
         cin >> op >> l >> r;
         if (op ==  || op == ) cin >> num;
         if (op == ) update1(, l, r, num);
         else if (op == ) update2(, l, r, num);
         else cout << query(, l, r) << endl;
     }
 }

 //Juddav007 0.0

（all)

THANKS FOR WATCHING!