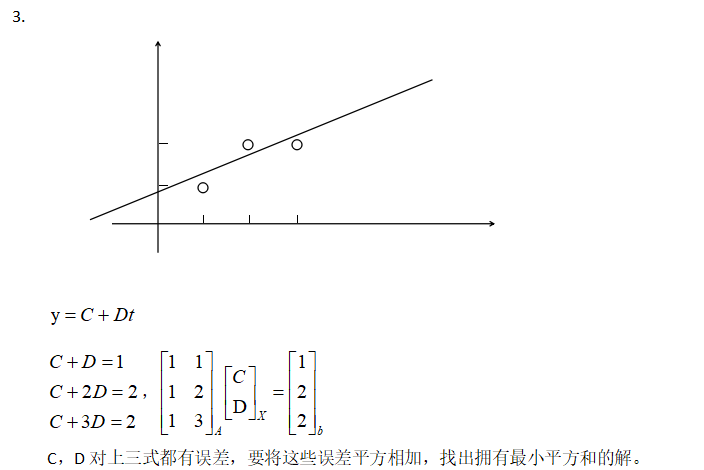
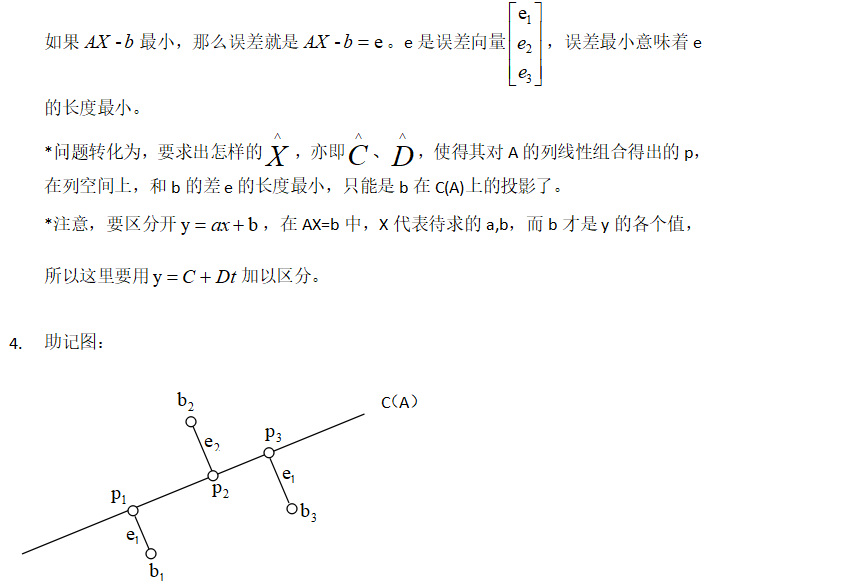
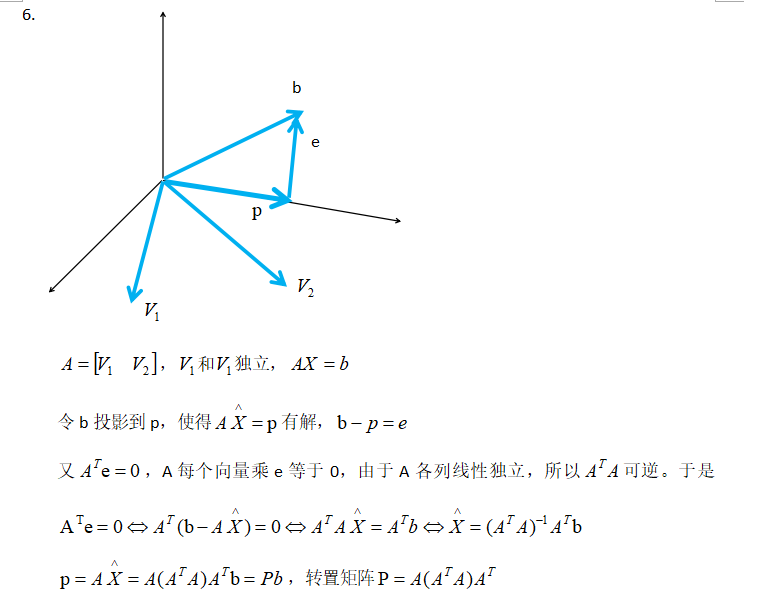
MIT线性代数：16.投影矩阵和最小二乘的更多相关文章

  1. 投影矩阵、最小二乘法和SVD分解

    投影矩阵广泛地应用在数学相关学科的各种证明中,但是由于其概念比较抽象,所以比较难理解.这篇文章主要从最小二乘法的推导导出投影矩阵,并且应用SVD分解,写出常用的几种投影矩阵的形式. 问题的提出 已知有 ...

  2. MIT线性代数：3.矩阵相乘

  3. 【脚下生根】之深度探索安卓OpenGL投影矩阵

    世界变化真快,前段时间windows开发技术热还在如火如荼,web技术就开始来势汹汹,正当web呈现欣欣向荣之际,安卓小机器人,咬过一口的苹果,winPhone开发平台又如闪电般划破了混沌的web世界 ...

  4. Android OpenGL ES(六)----进入三维在代码中创建投影矩阵和旋转矩阵

    我们如今准备好在代码中加入透视投影了. Android的Matrix类为它准备了两个方法------frustumM()和perspectiveM(). 不幸的是.frustumM()的个缺陷,它会影 ...

  5. WEBGL学习【八】模型视图投影矩阵

    <!--探讨WEBGL中不同图形的绘制方法:[待测试2017.11.6]--> <!DOCTYPE HTML> <html lang="en"> ...

  6. OpenGL投影矩阵(Projection Matrix)构造方法

    (翻译,图片也来自原文) 一.概述 绝大部分计算机的显示器是二维的(a 2D surface).在OpenGL中一个3D场景需要被投影到屏幕上成为一个2D图像(image).这称为投影变换(参见这或这 ...

  7. OpenGL投影矩阵

    概述 透视投影 正交投影 概述 计算机显示器是一个2D平面.OpenGL渲染的3D场景必须以2D图像方式投影到计算机屏幕上.GL_PROJECTION矩阵用于该投影变换.首先,它将所有定点数据从观察坐 ...

  8. (转)投影矩阵的推导(Deriving Projection Matrices)

    转自:http://blog.csdn.net/gggg_ggg/article/details/45969499 本文乃<投影矩阵的推导>译文,原文地址为: http://www.cod ...

  9. OpenGL中两种计算投影矩阵的函数

    OpenGL无意间同时看到两种创建投影矩阵的写法,可以说它们完成的是同样的功能,但写法完全不同,可以观摩一下什么叫做异曲同工之妙... 第一种: gltMakeShadowMatrix函数是重点 // ...

随机推荐

  1. K8s 从懵圈到熟练 – 集群网络详解

    作者 | 声东 阿里云售后技术专家 导读:阿里云 K8S 集群网络目前有两种方案:一种是 flannel 方案:另外一种是基于 calico 和弹性网卡 eni 的 terway 方案.Terway ...

  2. php 正则判断是否是手机号码 最新

    php 正则判断是否是手机号码 最新 标签: php正则 2013-09-22 14:31 55076人阅读 评论(1) 收藏 举报  分类: php(42)  版权声明:本文为博主原创文章,若转载请 ...

  3. bootstrap具体知识点(2)

    3.以移动设备为优先 <meta name=”viewport” content=”width=device-width,initial-scale=1,user-scalable=no”> ...

  4. web前端之移动端：知识汇

    移动前端自适应适配方法总结 移动端前端适配方案(总结) -- 面试重点 不要再问我移动适配的问题了 一.响应式布局: // Extra small devices (portrait phones, ...

  5. Android实现apk插件方式换肤

    换肤思路: 1.什么时候换肤? xml加载前换肤,如果xml加载后换肤,用户将会看见换肤之前的色彩,用户体验不好. 2.皮肤是什么? 皮肤就是apk,是一个资源包,包含了颜色.图片等. 3.什么样的控 ...

  6. python编程基础之九

    原码, 反码, 补码原码,即用二进制表示正数: 原码 == 反码 == 补码负数: 反码: 原码除符号位之外全部取反 补码: 反码 + 1 位运算:运算符 作用 & 按位与 | 按位或 ^ 按 ...

  7. MySQL基础（四）常用函数

    转载自 http://blog.csdn.net/evankaka MySQL数据库中提供了很丰富的函数.MySQL函数包括数学函数.字符串函数.日期和时间函数.条件判断函数.系统信息函数.加密函数. ...

  8. 像智能手机一样管理云端应用：阿里云联合微软全球首发开放应用模型（OAM）

    2019 年 10 月 17 日上午 9 点 15 分,阿里巴巴合伙人.阿里云智能基础产品事业部总经理蒋江伟在 QCon 上海<基于云架构的研发模式演进>主题演讲中,正式宣布: " ...

  9. Qt 找不到rc.exe

    Qt在window下出现编译错误: LINK : fatal error LNK1158: 无法运行“rc.exe” 解决: 找到rc.exe的放置路径,比如我的在下面: C:\Program Fil ...

  10. 初识AutoIt

    1.定义 AutoIt 目前最新是v3版本,这是一个使用类似BASIC脚本语言的免费软件,它设计用于Windows GUI(图形用户界面)中进行自动化操作.它利用模拟键盘按键,鼠标移动和窗口/控件的组 ...