B-Tree详解

之前写过一篇关于索引的文章《SQL夯实基础（五）：索引的数据结构》，这次我们主要详细讨论下B-Tree。

B-树

B-tree，即B树，而不要读成B减树，它是一种多路搜索树（并不是二叉的）：

1.定义任意非叶子结点最多只有M个儿子；且M>2；

2.根结点的儿子数为[2, M]；

3.除根结点以外的非叶子结点的儿子数为[M/2, M]；

4.每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）

5.非叶子结点的关键字个数=指向儿子的指针个数-1；

6.非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；

7.非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；

8.所有叶子结点位于同一层；

如：（M=3）

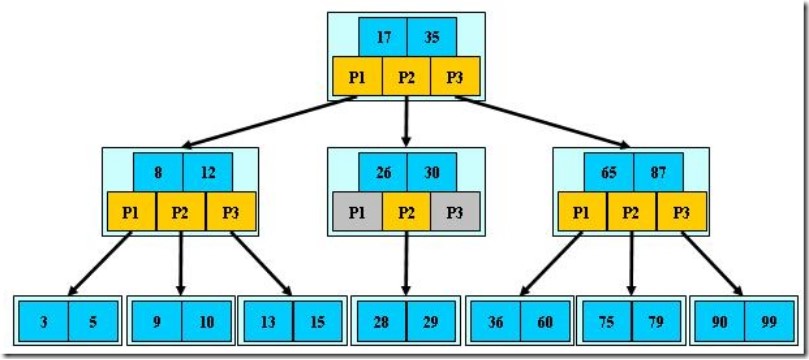
B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点；

B-树的特性：

1.关键字集合分布在整颗树中；

2.任何一个关键字出现且只出现在一个结点中；

3.搜索有可能在非叶子结点结束；

4.其搜索性能等价于在关键字全集内做一次二分查找；

5.自动层次控制；

　　由于限制了除根结点以外的非叶子结点，至少含有M/2个儿子，确保了结点的至少利用率，其最底搜索性能为：O（logN）

　　所以B-树的性能总是等价于二分查找（与M值无关），也就没有B树平衡的问题；

由于M/2的限制，在插入结点时，如果结点已满，需要将结点分裂为两个各占M/2的结点；删除结点时，需将两个不足M/2的兄弟结点合并；

---

B-树与二叉搜索树对比

基础：磁盘IO与预读

　　磁盘读取依靠的是机械运动，分为寻道时间、旋转延迟、传输时间三个部分，这三个部分耗时相加就是一次磁盘IO的时间，大概9ms左右。这个成本是访问内存的十万倍左右；正是由于磁盘IO是非常昂贵的操作，所以计算机操作系统对此做了优化：预读；每一次IO时，不仅仅把当前磁盘地址的数据加载到内存，同时也把相邻数据也加载到内存缓冲区中。因为局部预读原理说明：当访问一个地址数据的时候，与其相邻的数据很快也会被访问到。每次磁盘IO读取的数据我们称之为一页（page）。一页的大小与操作系统有关，一般为4k或者8k。这也就意味着读取一页内数据的时候，实际上发生了一次磁盘IO。

　　我们知道二叉查找树查询的时间复杂度是O（logN），查找速度最快和比较次数最少，既然性能已经如此优秀，但为什么实现索引是使用B-Tree而不是二叉查找树，关键因素是磁盘IO的次数。

数据库索引是存储在磁盘上，当表中的数据量比较大时，索引的大小也跟着增长，达到几个G甚至更多。当我们利用索引进行查询的时候，不可能把索引全部加载到内存中，只能逐一加载每个磁盘页，这里的磁盘页就对应索引树的节点。

二叉树

我们先来看二叉树查找时磁盘IO的次：定义一个树高为4的二叉树，查找值为10：

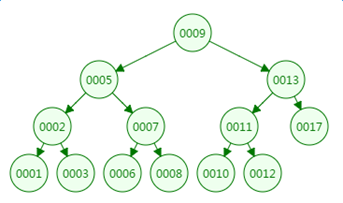
第一次磁盘IO：

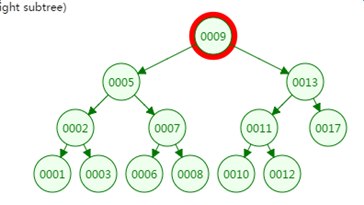
第二次磁盘IO

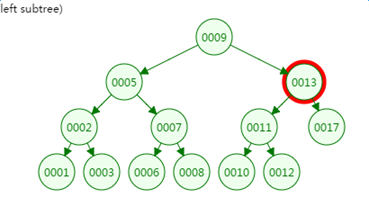
第三次磁盘IO:

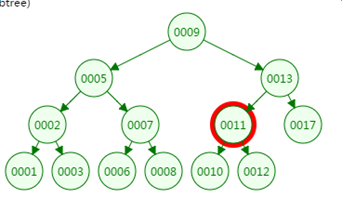
第四次磁盘IO：

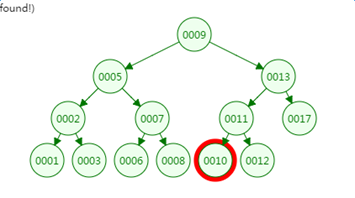
　　从二叉树的查找过程了来看，树的高度和磁盘IO的次数都是4，所以最坏的情况下磁盘IO的次数由树的高度来决定。

　　从前面分析情况来看，减少磁盘IO的次数就必须要压缩树的高度，让瘦高的树尽量变成矮胖的树，所以B-Tree就在这样伟大的时代背景下诞生了。

B-Tree

m阶B-Tree满足以下条件：

1、每个节点最多拥有m个子树

2、根节点至少有2个子树

3、分支节点至少拥有m/2颗子树（除根节点和叶子节点外都是分支节点）

4、所有叶子节点都在同一层、每个节点最多可以有m-1个key，并且以升序排列

如下有一个3阶的B树，观察查找元素21的过程：

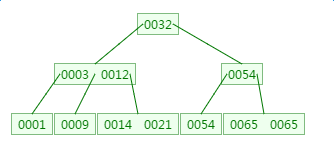
第一次磁盘IO：

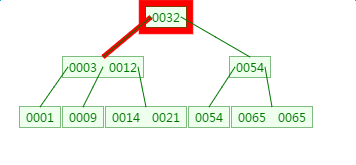
第二次磁盘IO：

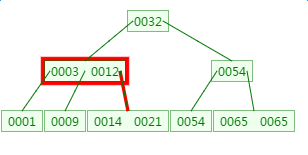
这里有一次内存比对：分别跟3与12比对

第三次磁盘IO:

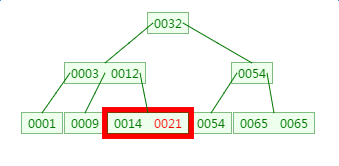
这里有一次内存比对，分别跟14与21比对

从查找过程中发现，B树的比对次数和磁盘IO的次数与二叉树相差不了多少，所以这样看来并没有什么优势。

但是仔细一看会发现，比对是在内存中完成中，不涉及到磁盘IO，耗时可以忽略不计。另外B树种一个节点中可以存放很多的key（个数由树阶决定）。

相同数量的key在B树中生成的节点要远远少于二叉树中的节点，相差的节点数量就等同于磁盘IO的次数。这样到达一定数量后，性能的差异就显现出来了。

---

B树的新增

在刚才的基础上新增元素4，它应该在3与9之间：

---

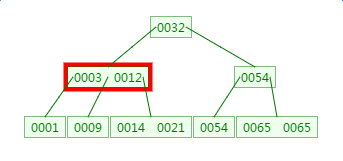
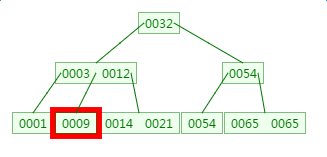
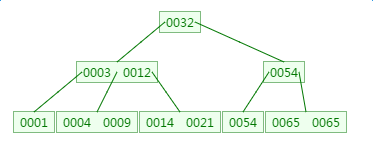
B树的删除

除元素9：

---

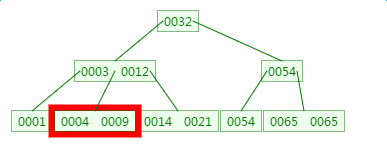
总结

　　插入或者删除元素都会导致节点发生裂变反应，有时候会非常麻烦，但正因为如此才让B树能够始终保持多路平衡，这也是B树自身的一个优势：自平衡。B树主要应用于文件系统以及部分数据库索引，如MongoDB，大部分关系型数据库索引则是使用B+树实现。