基于操作系统原理的Linux 系统的安装

---

---

一、实验目的

1．了解Linux操作系统的发行版本。

2．掌握Red Hat Linux 9.0的安装方法。

（可用Red Hat Linux 5.0版本替代9.0版本）

3．了解Linux其他版本（红旗Linux或Slackware Linux）的安装方法。

二、实验内容

1. 安装及配置VMWare(系统已安装，则此步跳过)

1)、完成新建虚拟机向导；

2）、VMWare的基础配置

2．VMware 下Linux 的安装

1）、启动安装程序，正式进入系统安装界面

2）、重新引导系统

三、实验平台

1．实验工具：Red Hat Linux 9.0（或红旗Linux、Slackware Linux）安装光盘。

2．实验设备：计算机一台，装有虚拟机系统VMWare，实验过程通过VMWare系统启Linux系统工作。

四、实验步骤

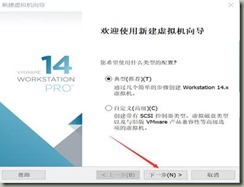
1. 安装及配置VMWare(系统已安装，则此步跳过)

1)、完成新建虚拟机向导。

点击创建新的虚拟机，在弹出的对话框中选择经典类型的配置并单击下一步，如图4-1所示；

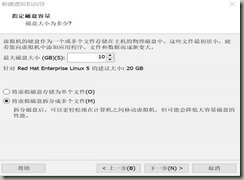
在安装来源中，选择稍后安装操作系统，并点击下一步；在安装系统类型中，选择Linux（L），同时其版本选择Red Hat Enterprise Linux 5，继续下一步；虚拟机的命名名称和安装位置，跳过。

这里由于实际实验机器的条件不同，可将最大磁盘大小调为10GB，选择“将虚拟磁盘拆分成多个文件”，如图4-2所示：

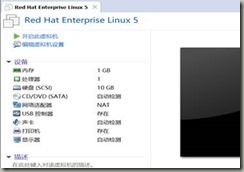
继续下一步，单击完成即可。

2）、VMWare的基础配置

在窗口中，单击“编辑虚拟机设置”，如图4-3所示：

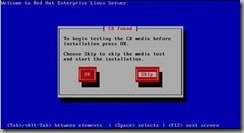
将虚拟机配置调整如下：

内存调整为4GB，有关虚拟机的处理器可根据实际条件自行调整，

重要的是在“CD/DVD(SATA)”中，将连接定位到系统镜像文件之后，单击确定即可。

2．VMware 下Linux 的安装

1）、启动安装程序，正式进入系统安装界面

将鼠标光标摄入窗口，并按下键盘“Enter”键，在弹出的界面中选择“Skip”选项并回车，如图4-4所示：

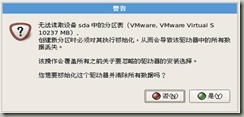
单击“下一步”，在系统语言中，根据实际情况选择简体中文，并一直继续“下一步”操作；在安装号码对话框中选择“跳过输入安装号码”，并确定和跳过。当对话框，跳出如图4-5的内容时，选择“是”：

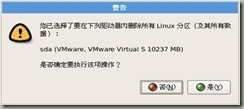
然后单击“下一步”, 当对话框，跳出如图4-6的内容时，选择“是”，之后一直默认下一步即可：

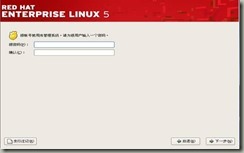
如图4-7所示，在为根账号输入密码时，可根据实际需要而定，在本例实验中，将root密码设置为：123456 ，一直默认“下一步”即可。

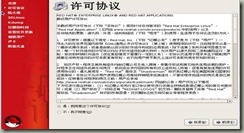
2）、重新引导系统

在上一步的基础上，单击“重新引导”即可进入系统的引导，这说明安装系统已基本完成。在“许可协议”中同意许可协议，并一直继续“前进”操作，本例实验将跳过新建用户步骤，如图4-8所示：

图4-8

五、运行结果

1. 安装及配置VMWare(系统已安装，则此步跳过)

当单击“开启此虚拟机”，能成功弹出如图5-1所示的内容，则说明完成了新建虚拟机向导和VMWare的基础配置：

2．VMware 下Linux 的安装

由重新引导对话框提示可知，系统的基本安装已经完成，如图5-2所示：

当界面出现如图5-3的内容，则说明本实验已经正确完成操作。

六、实验总结

经过本实验，得以丰富经验，可总结如下：

1、 系统之所以不能从光盘启动，在于“启动时连接”一项没有被选中了、硬件设备本身就没有光盘、或者是选择虚拟设备节点没有选择为IDE；

2、 本例实验虽然顺畅，但此处依旧为大家总结安装Red Hat Linux过程中常出现的问题。

如：启动虚拟机，弹出一个框“已将该虚拟机配置为使用 64 位客户机操作系统。但是，无法执行 64 位操作。此主机支持 Intel VT-x，但 Intel VT-x 处于禁用状态。如果已在 BIOS/固件设置中禁用 Intel VT-x，或主机自更改此设置后从未重新启动，则 Intel VT-x 可能被禁用。

(1) 确认 BIOS/固件设置中启用了 Intel VT-x 并禁用了“可信执行”。

(2) 如果这两项 BIOS/固件设置有一项已更改，请重新启动主机。

(3) 如果您在安装 VMware Workstation 之后从未重新启动主机，请重新启动。

(4) 将主机的 BIOS/固件更新至最新版本。”

3、红旗Linux与 Red Hat Linux主要区别在于，用途的不一样。如：红旗LINUX主要应用于服务器方面，而Red Hat Linux能够把Linux和开源技术以及企业级的培训、技术支持和咨询融合得如此美妙。