E-triples II_2019牛客暑期多校训练营（第四场）

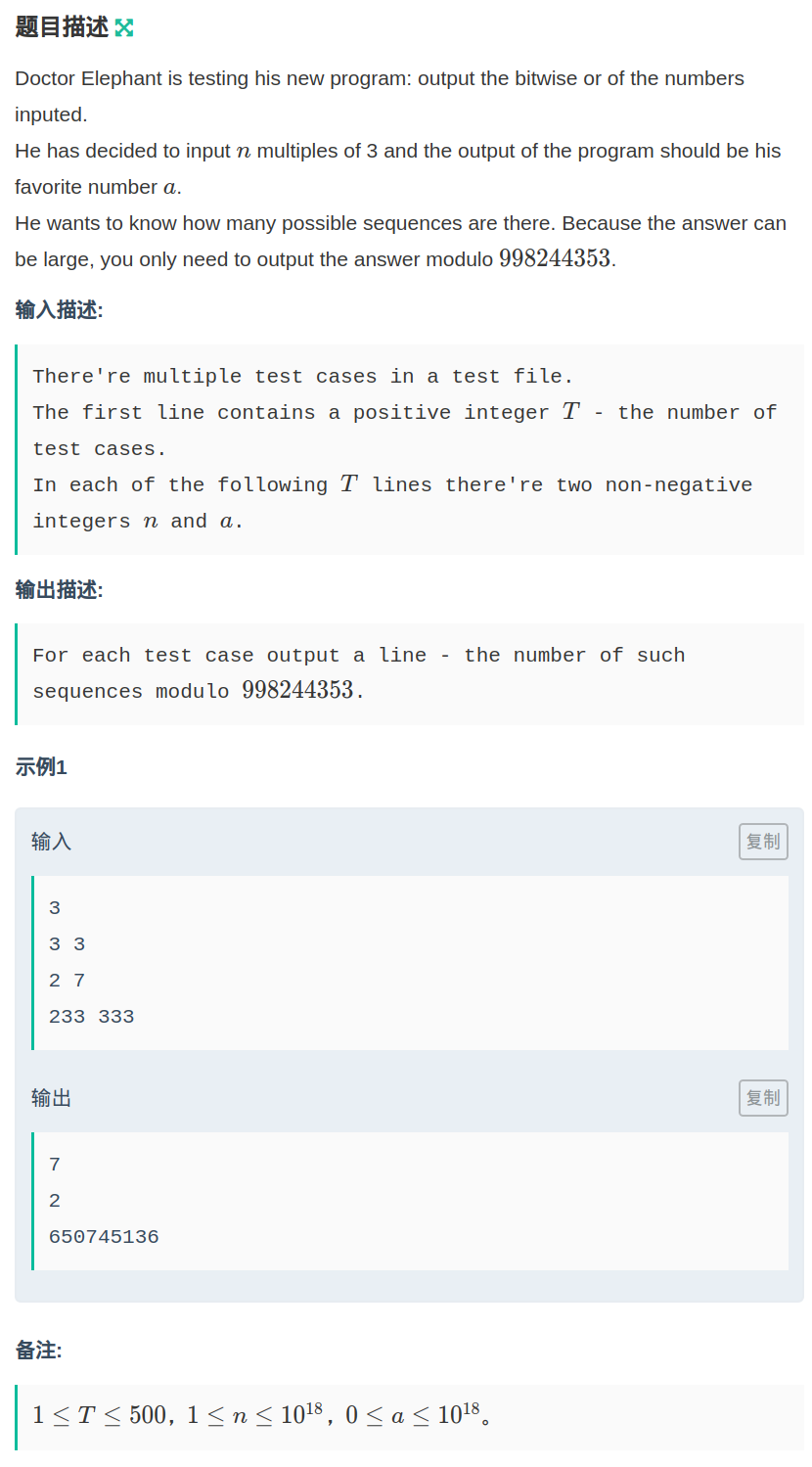
求用n个3的倍数的数按位或出数字a的方案数有多少种（0也算3的倍数）

题解

• 若数b的每个二进制位上的1，在a中也为1，则称b为a的子集
• 容易知道任意个a的子集按位或出来的结果还是a的子集
• 若问题改为按位或出来的结果是a的子集的方案数，那么答案就是a的子集中是3的倍数的子集个数的n次方
  
  接着我们对子集按二进制上的1 mod 3的个数划分，例如1101有两个1mod3=1, 一个1mod3 = 2，设\(S[i][j]\)表示a的子集中有i个mod3=1，j个mod3=2的子集的子集 中是3的倍数的个数，例如a = 1101的一个子集1001表示的状态为\(S[1][1]\), 1001的子集中是3的倍数的有1001和0000所以\(S[1][1] = 2\)，那么\(S[i][j]\)的n次方就可以表示为用n个3的倍数的数按位或出来的结果的状态是S[i][j]的子集方案数
  
  那么\(\sum_{i=1}^kS[i][k-i]\)就表示或出来的结果最多匹配上a中K个1的方案数，那么我们就可以用最多匹配上a中K个1的方案数，减去匹配上a中K-1个1的方案数得出答案，但是这样简单的相减是不行的因为\(S[i][k-i]\)的子集是会有重叠的，会多扣掉最多匹配k-2个1的方案数，根据容斥原理应当减去最多匹配K-1的方案数，加上最多匹配K-2的方案数，扣掉K-3加上K-4...

代码

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
const int mx = 65;
const ll mod = 998244353;
int C[mx][mx], S[mx][mx];

ll pow_mod(ll a, ll b) {
    ll ans = 1;
    while (b > 0) {
        if (b & 1) ans = ans * a % mod;
        a = a * a % mod;
        b /= 2;
    }
    return ans;
}

int main() {
    C[0][0] = 1;
    for (int i = 1; i < mx; i++) {
        C[i][0] = 1;
        for (int j = 1; j <= i; j++) {
            C[i][j] = (C[i-1][j-1] + C[i-1][j]) % mod;
        }
    }

    for (int i = 0; i < mx; i++) {
        for (int j = 0; j < mx; j++) {
            for (int p = 0; p <= i; p++) {
                for (int q = 0; q <= j; q++) {
                    if ((p + 2*q) % 3 != 0) continue;
                    S[i][j] += C[i][p] * C[j][q] % mod;
                    S[i][j] %= mod;
                }
            }
        }
    }
    S[0][0] = 1;

    int T;
    scanf("%d", &T);

    while (T--) {
        ll n, a, x = 0, y = 0;
        scanf("%lld%lld", &n, &a);
        for (int i = 0; i < 64; i++) {
            if (a & (1LL<<i)) {
                if (i % 2 == 0) x++;
                else y++;
            }
        }
        ll ans = 0;
        for (int i = 0; i <= x; i++) {
            for (int j = 0; j <= y; j++) {
                ll tmp = C[x][i] * C[y][j] % mod * pow_mod(S[i][j], n) % mod;
                if ((x+y-i-j) % 2) tmp *= -1;
                ans = (ans + tmp) % mod;
            }
        }
        ans = (ans + mod) % mod;
        printf("%lld\n", ans);
    }
    return 0;
}