哈夫曼树C++实现详解

哈夫曼树的介绍

Huffman Tree，中文名是哈夫曼树或霍夫曼树，它是最优二叉树。

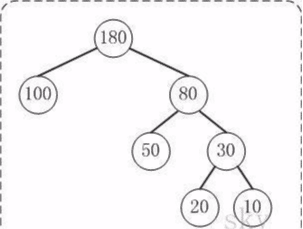
定义：给定n个权值作为n个叶子结点，构造一棵二叉树，若树的带权路径长度达到最小，则这棵树被称为哈夫曼树。 这个定义里面涉及到了几个陌生的概念，下面就是一颗哈夫曼树，我们来看图解答。

(01) 路径和路径长度

定义：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。

例子：100和80的路径长度是1，50和30的路径长度是2，20和10的路径长度是3。

(02) 结点的权及带权路径长度

定义：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。

例子：节点20的路径长度是3，它的带权路径长度= 路径长度 * 权 = 3 * 20 = 60。

(03) 树的带权路径长度

定义：树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL。

例子：示例中，树的WPL= 1*100 + 2*80 + 3*20 + 3*10 = 100 + 160 + 60 + 30 = 350。

比较下面两棵树

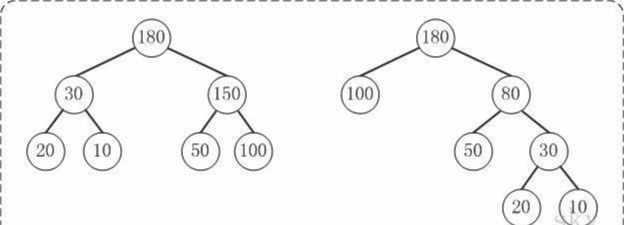
上面的两棵树都是以{10, 20, 50, 100}为叶子节点的树。

左边的树WPL=2*10 + 2*20 + 2*50 + 2*100 = 360

右边的树WPL=350

左边的树WPL > 右边的树的WPL。你也可以计算除上面两种示例之外的情况，但实际上右边的树就是{10,20,50,100}对应的哈夫曼树。至此，应该堆哈夫曼树的概念有了一定的了解了，下面看看如何去构造一棵哈夫曼树。

哈夫曼树的图文解析

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，哈夫曼树的构造规则为：

1. 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；

2. 在森林中选出根结点的权值最小的两棵树进行合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；

3. 从森林中删除选取的两棵树，并将新树加入森林；

4. 重复(02)、(03)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

以{5,6,7,8,15}为例，来构造一棵哈夫曼树。

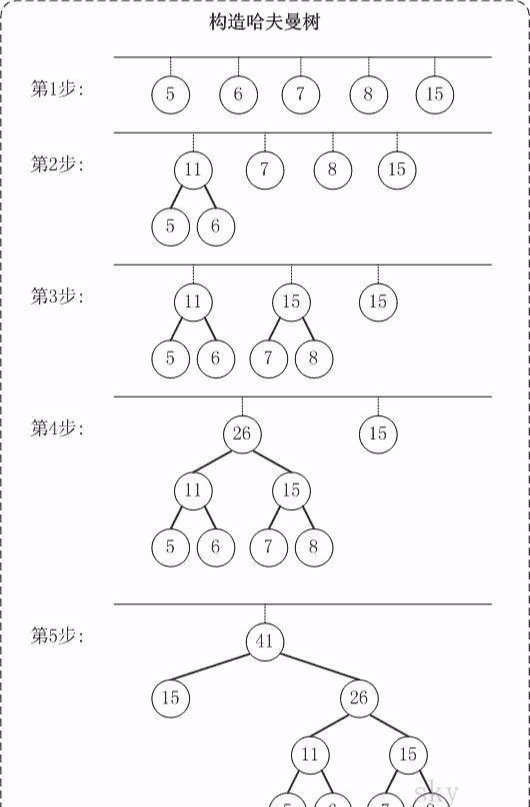
第1步：创建森林，森林包括5棵树，这5棵树的权值分别是5,6,7,8,15。

第2步：在森林中，选择根节点权值最小的两棵树(5和6)来进行合并，将它们作为一颗新树的左右孩子(谁左谁右无关紧要，这里，我们选择较小的作为左孩子)，并且新树的权值是左右孩子的权值之和。即，新树的权值是11。 然后，将"树5"和"树6"从森林中删除，并将新的树(树11)添加到森林中。

第3步：在森林中，选择根节点权值最小的两棵树(7和8)来进行合并。得到的新树的权值是15。 然后，将"树7"和"树8"从森林中删除，并将新的树(树15)添加到森林中。

第4步：在森林中，选择根节点权值最小的两棵树(11和15)来进行合并。得到的新树的权值是26。 然后，将"树11"和"树15"从森林中删除，并将新的树(树26)添加到森林中。

第5步：在森林中，选择根节点权值最小的两棵树(15和26)来进行合并。得到的新树的权值是41。 然后，将"树15"和"树26"从森林中删除，并将新的树(树41)添加到森林中。

此时，森林中只有一棵树(树41)。这棵树就是我们需要的哈夫曼树！

哈夫曼树的基本操作

哈夫曼树的重点是如何构造哈夫曼树。本文构造哈夫曼时，用到了以前介绍过的"(二叉堆)最小堆"。下面对哈夫曼树进行讲解。

1. 基本定义

GIF

template <class T>class HuffmanNode{ public: T key; // 权值 HuffmanNode *left; // 左孩子 HuffmanNode *right; // 右孩子 HuffmanNode *parent;// 父结点 HuffmanNode(){} HuffmanNode(T value, HuffmanNode *l, HuffmanNode *r, HuffmanNode *p): key(value),left(l),right(r),parent(p) {}};

HuffmanNode是哈夫曼树的节点类。

template <class T>class Huffman { private: HuffmanNode<T> *mRoot; // 根结点 public: Huffman(); ~Huffman(); // 前序遍历"Huffman树" void preOrder(); // 中序遍历"Huffman树" void inOrder(); // 后序遍历"Huffman树" void postOrder(); // 创建Huffman树 void create(T a[], int size); // 销毁Huffman树 void destroy(); // 打印Huffman树 void print(); private: // 前序遍历"Huffman树" void preOrder(HuffmanNode<T>* tree) const; // 中序遍历"Huffman树" void inOrder(HuffmanNode<T>* tree) const; // 后序遍历"Huffman树" void postOrder(HuffmanNode<T>* tree) const; // 销毁Huffman树 void destroy(HuffmanNode<T>* &tree); // 打印Huffman树 void print(HuffmanNode<T>* tree, T key, int direction);};

Huffman是哈夫曼树对应的类，它包含了哈夫曼树的根节点和哈夫曼树的相关操作。

2. 构造哈夫曼树

/* * 创建Huffman树 * * 参数说明： * a 权值数组 * size 数组大小 * * 返回值： * Huffman树的根节点 */template <class T>void Huffman<T>::create(T a[], int size){ int i; HuffmanNode<T> *left, *right, *parent; MinHeap<T> *heap = new MinHeap<T>(); // 建立数组a对应的最小堆 heap->create(a, size); for(i=0; i<size-1; i++) { left = heap->dumpFromMinimum(); // 最小节点是左孩子 right = heap->dumpFromMinimum(); // 其次才是右孩子 // 新建parent节点，左右孩子分别是left/right； // parent的大小是左右孩子之和 parent = new HuffmanNode<T>(left->key+right->key, left, right, NULL); left->parent = parent; right->parent = parent; // 将parent节点数据拷贝到"最小堆"中 if (heap->copyOf(parent)!=0) { cout << "插入失败!" << endl << "结束程序" << endl; destroy(parent); parent = NULL; break; } } mRoot = parent; // 销毁最小堆 heap->destroy(); delete heap;}

首先通过heap->create(a, size)来创建最小堆。最小堆构造完成之后，进入for循环。

每次循环时：

(01) 首先，将最小堆中的最小节点拷贝一份并赋值给left，然后重塑最小堆(将最小节点和后面的节点交换位置，接着将"交换位置后的最小节点"之前的全部元素重新构造成最小堆)；

(02) 接着，再将最小堆中的最小节点拷贝一份并将其赋值right，然后再次重塑最小堆；

(03) 然后，新建节点parent，并将它作为left和right的父节点；

(04) 接着，将parent的数据复制给最小堆中的指定节点。

在二叉堆中已经介绍过堆，这里就不再对堆的代码进行说明了。