之前我们知道，方差是一组数据的离散程度，它的公式为：

那么如果我们有几组数据，需要知道这几组数据的协同性呢？

举个例子，还是在小红，几次考试成绩如下：

入学考试：数学：80，语文：80

期中考试：数学：90，语文：70

期末考试：数学：70，语文：90

小蓝，几次考试成绩如下：

入学考试：数学：60，语文：60

期中考试：数学：70，语文：70

期末考试：数学：80，语文：80

好，我们把数据放着，先说一下概念。所谓的协方差，就是用来统计两组数据之间的协同程度，协方差矩阵是用来遍历不同组数据的方差。

协方差用公式表示为：

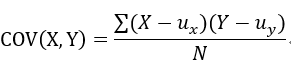
方差是协方差的特殊表现形式，即X=Y的时候。

OK，我们现在再来看上面的数据，根据这个公式，计算小红数学和总分的协方差为：

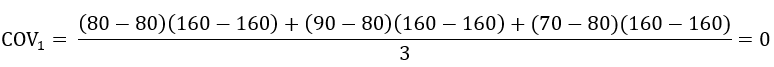
计算小蓝数学和总分的协方差为：

从这些数据上可以看出，小红的协方差为0，表明数学和总分没有什么关系，因为他的数学考得好，语文就考的不好。但小蓝的协方差是正的，表示他的数学进步，语文也跟着进步，总分自然提高了，是个全面发展的好青年。

那么我们想全面的表现语文、数学、总分之间的相关性，该如何表示呢？嗯，有个东西叫协方差矩阵，它可以表示多组数据之间两两之间的协方差。

比如按上面小红的数学成绩和总分的关系，形成数据集

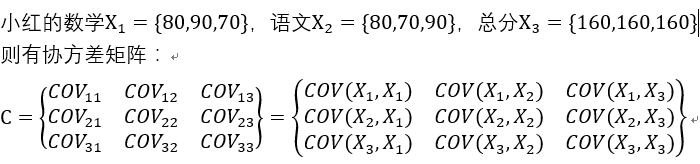
SLAM的数学基础（2）：协方差和协方差矩阵的更多相关文章

  1. 方差variance, 协方差covariance, 协方差矩阵covariance matrix

    https://www.jianshu.com/p/e1c8270477bc?utm_campaign=maleskine&utm_content=note&utm_medium=se ...

  2. 方差variance, 协方差covariance, 协方差矩阵covariance matrix | scatter matrix | weighted covariance | Eigenvalues and eigenvectors

    covariance, co本能的想到双变量,用于描述两个变量之间的关系. correlation,相关性,covariance标准化后就是correlation. covariance的定义: 期望 ...

  3. 视觉SLAM的数学基础 第一篇 3D空间的位置表示

    视觉SLAM中的数学基础 第一篇 3D空间的位置表示 前言 转眼间一个学期又将过去,距离我上次写<一起做RGBD SLAM>已经半年之久.<一起做>系列反响很不错,主要由于它为 ...

  4. SLAM的数学基础（4）：先验概率、后验概率、贝叶斯准则

    假设有事件A和事件B,可以同时发生但不是完全同时发生,如以下韦恩图所示: 其中,A∩B表示A和B的并集,即A和B同时发生的概率. 如此,我们很容易得出,在事件B发生的情况下,事件A发生的概率为: 这个 ...

  5. SLAM的数学基础（3）：几种常见的概率分布的实现及验证。

    分布,在计算机学科里一般是指概率分布,是概率论的基本概念之一.分布反映的是随机或某个系统中的某个变量,它的取值的范围和规律. 常见的分布有:二项分布.泊松分布.正态分布.指数分布等,下面对它们进行一一 ...

  6. SLAM的数学基础（1）：什么是方差，有什么意义？

    小红班上有两组同学的数学考试分数为: 第一组:小红:100分,小明:60分,小宇:20分 第二组:小蓝:70分,小华:60分,小杰:50分 那么很容易算出,第一组的平均分是60分,第二组的平均分也是6 ...

  7. 自主移动机器人同时定位与地图创建（SLAM）方法概述

    1.引言: 机器人的研究越来越多的得到关注和投入,随着计算机技术和人工智能的发展,智能自主移动机器人成为机器人领域的一个重要研究方向和研究热点.移动机器人的定位和地图创建是自主移动机器人领域的热点研究 ...

  8. 协方差（Covariance）

    统计学上用方差和标准差来度量数据的离散程度 ,但是方差和标准差是用来描述一维数据的(或者说是多维数据的一个维度),现实生活中我们常常会碰到多维数据,因此人们发明了协方差(covariance),用来度 ...

  9. 向量的表示及协方差矩阵 （PCA的理论基础）

    原文:http://blog.csdn.net/songzitea/article/details/18219237 引言 当面对的数据被抽象为一组向量,那么有必要研究一些向量的数学性质.而这些数学性 ...

随机推荐

  1. GPU端到端目标检测YOLOV3全过程（下）

    GPU端到端目标检测YOLOV3全过程(下) Ubuntu18.04系统下最新版GPU环境配置 安装显卡驱动 安装Cuda 10.0 安装cuDNN 1.安装显卡驱动 (1)这里采用的是PPA源的安装 ...

  2. Postman 的基本功能按钮解释、发送post请求及get请求、查看响应信息

    一.界面功能按钮: 二.postman模拟发送post请求: 三.postman模拟get请求: 选择请求类型-->输入请求URL-->点击send发送 四.查看响应信息

  3. 【NX二次开发】Block UI 选项卡控件

    [NX二次开发]Block UI 选项卡控件

  4. sql优化问题

    一.分析阶段 一 般来说,在系统分析阶段往往有太多需要关注的地方,系统各种功能性.可用性.可靠性.安全性需求往往吸引了我们大部分的注意力,但是,我们必须注意,性能 是很重要的非功能性需求,必须根据系统 ...

  5. JAVA设计模式（6：单例模式详解）

    单例模式作为一种创建型模式,在日常开发中用处极广,我们先来看一一段代码: // 构造函数 protected Calendar(TimeZone var1, Locale var2) { this.l ...

  6. 机器人路径规划其二 A-Star Algorithm【附动态图源码】

    首先要说明的是,机器人路径规划与轨迹规划属于两个不同的概念,一般而言,轨迹规划针对的对象为机器人末端坐标系或者某个关节的位置速度加速度在时域的规划,常用的方法为多项式样条插值,梯形轨迹等等,而路径规划 ...

  7. Oracle数据泵导出数据库

    Oracle数据泵导出数据库 特别注意:如果后续要导入的数据库版本低,所有导出命令就需要在后面加一个version=指定版本. 例如从11g导出数据导入到10g,假设10g具体版本为10.2.0.1, ...

  8. 安聊服务端Netty的应用

    Netty简介 Netty是一个面向网络编程的Java基础框架,它基于异步的事件驱动,并且内置多种网络协议的支持,可以快速地开发可维护的高性能的面向协议的服务器和客户端. 安聊简介 安聊是一个即时聊天 ...

  9. 乘风破浪，Java遇见OpenJDK GA(Build By Microsoft)，即将晋升为Azure云管理服务默认JVM

    什么是Microsoft Build of OpenJDK Java Development Kit (JDK) 是Sun公司(已被Oracle收购)针对Java开发员的软件开发工具包.自从Java推 ...

  10. 解决WebStorm开发vue提示Module is not installed、Unresolved variable or type

    WebStorme2021.1版本: Setting->Languages->JavaScript->Webpack由原先的disable选为Automatically即可(右下角弹 ...