Codeforces 506E - Mr. Kitayuta's Gift（神仙矩阵乘法）

Codeforces 题目传送门 & 洛谷题目传送门

神仙题 %%%%%%%%%%%%%

u1s1 感觉这道题风格很省选（

下记 \(m=|s|\)，首先探讨 \(n+m\) 为偶数的情形。

首先考虑一个暴力的 DP，我们设 \(dp_{i,l,r}\) 表示当前考虑了回文串的前 \(i\) 个字符和后 \(i\) 个字符，前 \(i\) 个字符恰好匹配了 \(s\) 的 \([1,l-1]\) 区间中的字符，后 \(i\) 个字符恰好匹配了 \(s\) 的 \([r+1,m]\) 区间中的字符的方案数，再记 \(g_i\) 为当前考虑了回文串的前 \(i\) 个字符和后 \(i\) 个字符。

考虑转移，分四种情况：

1. \(r-l\le 1\) 且 \(s_l=s_r\)，那么如果我们在 \(i+1\) 位置填上 \(s_l\) 那么就匹配结束了，即 \(g_{i+1}\leftarrow dp_{i,l,r}\)，否则还是只能完全匹配 \([1,l-1]\) 和 \([r+1,n]\) 中的字符，即 \(dp_{i+1,l,r}\leftarrow 25·dp_{i,l,r}\)。
2. \(r-l\ge 2\) 且 \(s_l=s_r\)，那么如果我们在从左往右数和从右往左数第 \(i+1\) 的位置填上 \(s_l\) 就可以匹配到 \([1,l]\) 和 \([r,m]\)，即 \(dp_{i+1,l+1,r-1}\leftarrow dp_{i,l,r}\)，否则还是有 \(dp_{i+1,l,r}\leftarrow 25·dp_{i,l,r}\)
3. \(s_l\ne s_r\)，那么如果我们在从左往右数和从右往左数第 \(i+1\) 的位置填 \(s_l\)，左端点就可以多匹配一位，即 \(dp_{i+1,l+1,r}\leftarrow dp_{i,l,r}\)，同理如果我们填 \(s_r\)，右端点就可以多匹配一位，即 \(dp_{i+1,l,r-1}\leftarrow dp_{i,l,r}\)，否则还是只能完全匹配 \([1,l-1]\) 和 \([r+1,n]\) 中的字符，即 \(dp_{i+1,l,r}\leftarrow 24·dp_{i,l,r}\)。
4. \(g\) 的转移：显然由于我们已经匹配结束了，剩下的位置填什么都行，即 \(g_{i+1}\leftarrow 26·g_i\)。

最终答案即为 \(g_{(n+m)/2}\)

这样暴力是 \(nm^2\) 的，如果强行把 \((l,r)\) 看作一个二元组套矩乘，那可以实现 \(m^6\log n\) 的优秀复杂度，一脸过不去。

我们考虑优化，敏感一些的同学应该可以注意到这个 DP 转移方程有点像 DAG 上的 DP，事实上，如果我们把所有二元组 \((l,r)\) 以及 \(g_i\)（下记为目标点）分别看作一个点，对于形如 \(dp_{i+1,x}\leftarrow z·dp_{i,y}\) 的状态转移方程式，我们就从 \(y\) 到 \(x\) 连 \(z\) 条边，那么答案就是 \((1,m)\) 表示的点到目标点的经过 \(\dfrac{n+m}{2}\) 条边的路径条数。

我们考虑探究一下这张图长啥样，比方说 \(s=\text{abaac}\)，那么建出图来就长这样（这里借用了 xht37 大佬题解里的图）：

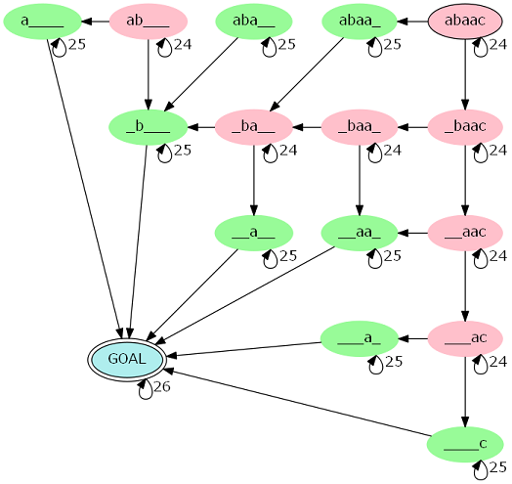
不难发现，该图是由若干个自环即若干条有向边组成了，对于每个状态 \((l,r)\) 都有一个自环连向自己，如果去掉这些自环，那形成的图显然是一个 DAG（\((l,r)\) 能到达 \((l',r')\) 当且仅当 \([l',r']\subseteq[l,r]\)，这显然构成了一个偏序关系），也就是说从源点 \((1,m)\) 到目标点，经过的非自环边的个数最多只有 \(m\)（每次经过一条边，区间长度缩小 \(1\) 或 \(2\)，因此至少缩小 \(m\) 次就能到达目标点）

并且还可以发现除了目标点上有个 \(26\) 的自环之外，自环的类型只有 \(2\) 种，那就是权值为 \(25\) 的环和权值为 \(24\) 的环，我们不妨称存在权值为 \(25\) 的自环连向自己的点为“\(25\) 点”，其余的点称为“\(24\) 点”。考虑观察这个路径个数有什么性质，我们不妨称去掉自环边后路径相同的路径为等价类，考虑对每个等价类计算一遍方案数，容易发现等价类具体先经过权值为多少的自环，后经过权值为多少的自环并不重要，我们只关心它经过了多少权值为 \(24,25,26\) 的自环，即两个等价类的路径的个数相同当且仅当这两个等价类的路径上 \(24,25,26\) 的自环的个数相同。

显然权值为 \(26\) 的自环就是废话，因为从起始点到目标点总共只会经过一个 \(26\) 的自环。而经过的 \(25\) 的自环和 \(24\) 的自环个数有一个性质，那就是如果我们记经过的 \(25\) 的自环个数为 \(c_{25}\)，经过的 \(24\) 的自环个数为 \(c_{24}\)，则 \(c_{25}=\lceil\dfrac{s-c_{24}}{2}\rceil\)，道理很简单，对于一个 \(25\) 点 \([l,r]\)，每当我们从该点走向一个别的点时，区间长度会缩短 \(2\)（当然 \(l=r\) 时只会缩短 \(1\)），而对于一个 \(24\) 点 \([l,r]\) 则会缩短 \(1\)，因此 \(c_{25}=\lceil\dfrac{s-c_{24}}{2}\rceil\)，故我们只需对于每个 \(i\) 求出经过 \(i\) 个 \(24\) 点的等价类个数，然后对每个 \(i\) 跑一遍矩阵快速幂即可。

这个东西怎么求呢？考虑记忆化搜索，记 \(f_{x,l,r}\) 为以状态 \([l,r]\) 为结尾的经过 \(x+[(l,r)\text{是否为}24\text{点}]\) 个 \(24\) 点的路径个数，转移很容易，如果 \(s_{l-1}\ne s_r\) 那 \((l-1,r)\) 为 \(24\) 点并且存在 \((l-1,r)\to (l,r)\) 的边，\(f_{x,l,r}\leftarrow f_{x,l,r}\)，\((l,r+1)\) 也同理，如果 \(s_{l-1}=s_{r+1}\)，那 \((l-1,r+1)\) 为 \(25\) 点并且存在 \((l-1,r+1)\to(l+r)\) 的边，\(f_{x,l,r}\leftarrow f_{x,l-1,r+1}\)，记忆化搜索即可，边界条件 \(f_{0,1,m}=1\)。

这样复杂度是 \(m^4\log n\) 的，还是无法通过，继续优化。

这题复杂度瓶颈在于对于每个 \(x\) 都跑一遍矩阵优化，考虑对状态进行压缩，我们在上面建一排 \(m\) 个 \(24\) 点，在下面建一排 \(\lceil\dfrac{m}{2}\rceil\) 个 \(25\) 点，对于上面一排的第 \(i\) 个点，连一条指向第二排第 \(\lceil\dfrac{m}{2}\rceil-\lceil\dfrac{m-i}{2}\rceil\) 个节点，权值为经过 \(i\) 个路径的等价类个数，然后在相邻的 \(24\) 点之间连权值为 \(1\) 的边，在相邻的 \(25\) 点之间连权值为 \(1\) 的边，然后每个 \(24\) 点上都套个权值为 \(24\) 的自环，每个 \(25\) 点上套个权值为 \(25\) 的自环，最后连一条从最右边的 \(25\) 点向目标点，权值为 \(1\) 的边，再在目标点上套个 \(26\) 的自环即可。这里还是借一张 xht37 神仙题解里的图：

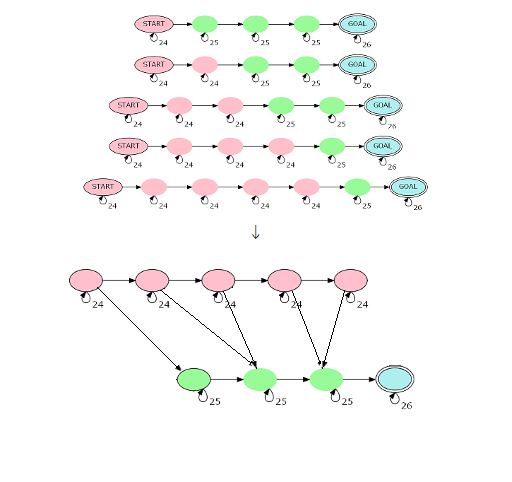
这样状态数降低到了 \(\mathcal O(m)\)，跑一遍矩乘即可，复杂度 \(m^3\log n\)。

这仅仅只是 \(n+m\) 为偶数的情况，最后考虑 \(n+m\) 为奇数的情况有什么不同。记 \(p=\dfrac{n+m-1}{2}\)，唯一的不同就是最后一步，\(dp_{p,i,i+1}\)（\(s_i=s_{i+1}\)），无法转移到 \(g_{p+1}\)。正难则反，我们考虑拿总方案数减去这部分方案数，我们只需保留最后一步从 \((i,i+1)\) 转移的链，并去掉目标点上 \(26\) 的自环即可。

最后，此题还存在卡常数的问题。这里有一个小技巧，那就是由于我们只在 \((i,j)(i<j)\) 的状态之间连边，得到的矩阵是一个下三角矩阵（我代码里使用的是先矩阵、后向量的乘法，因此对于存在边的 \((i,j)\) 我是令 \(j\) 为行号 \(i\) 为列号，因此得到的是上三角矩阵，不过差不多辣），因此我们在矩阵乘法时候只需枚举 \(1\le i\le k\le j\) 的 \((i,j,k)\)，这样常数可以减小到原来的 \(\dfrac{1}{6}\)

u1s1 这题题解码死我了

话说这场的 D1C D E 我是不是都做过了啊，u1s1 这场的 C 我都不会。

const int MAXN=200;
const int MAXM=300;
const int MOD=1e4+7;
int n,m,k;char s[MAXN+5];
struct mat{
	ll a[MAXM+5][MAXM+5];
	mat(){memset(a,0,sizeof(a));}
	mat operator *(const mat &rhs){
		mat res;
		for(int i=1;i<=k;i++) for(int l=1;l<=i;l++) for(int j=1;j<=l;j++)
			res.a[i][j]+=a[i][l]*rhs.a[l][j];
		for(int i=1;i<=k;i++) for(int j=1;j<=k;j++) res.a[i][j]%=MOD;
		return res;
	}
};
int dp[MAXN+5][MAXN+5][MAXN+5];
int dfs(int x,int l,int r){
	if(x<0) return 0;
	if(~dp[x][l][r]) return dp[x][l][r];
	if(l==1&&r==m) return dp[x][l][r]=(!x);
	dp[x][l][r]=0;
	if(l!=1&&s[l-1]!=s[r]) dp[x][l][r]=(dp[x][l][r]+dfs(x-1,l-1,r))%MOD;
	if(r!=m&&s[l]!=s[r+1]) dp[x][l][r]=(dp[x][l][r]+dfs(x-1,l,r+1))%MOD;
	if(l!=1&&r!=m&&s[l-1]==s[r+1]) dp[x][l][r]=(dp[x][l][r]+dfs(x,l-1,r+1))%MOD;
	return dp[x][l][r];
}
int main(){
	scanf("%s%d",s+1,&n);m=strlen(s+1);k=m+((m+1)>>1);
	memset(dp,-1,sizeof(dp));mat st,trs,res;
	for(int i=0;i<m;i++){
		int cnt=0;
		for(int j=1;j<=m;j++){
			cnt=(cnt+dfs(i,j,j))%MOD;
			if((j^m)&&!(s[j]^s[j+1])) cnt=(cnt+dfs(i,j,j+1))%MOD;
		}
//		printf("%d %d\n",i,cnt);
		if(i) trs.a[k-((m-i+1)>>1)][i]=cnt;
		else st.a[m][1]=cnt;
	}
	for(int i=2;i<m;i++) trs.a[i][i-1]=1;
	if(m>1) st.a[1][1]=1;
	for(int i=m;i<k;i++) trs.a[i+1][i]=1;
	for(int i=1;i<m;i++) trs.a[i][i]=24;
	for(int i=m;i<k;i++) trs.a[i][i]=25;
	trs.a[k][k]=26;
	for(int i=1;i<=k;i++) res.a[i][i]=1;
//	for(int i=1;i<=k;i++) for(int j=1;j<=k;j++) printf("%d%c",trs.a[i][j],(j==k)?'\n':' ');
	int stp=(n+m+1)>>1;
	for(;stp;stp>>=1,trs=trs*trs) if(stp&1) res=res*trs;
//	for(int i=1;i<=k;i++) for(int j=1;j<=k;j++) printf("%d%c",res.a[i][j],(j==k)?'\n':' ');
	int sum=0;for(int i=1;i<=k;i++) sum=(sum+st.a[i][1]*res.a[k][i])%MOD;
	if(!((n+m)&1)) return printf("%d\n",sum),0;
	int ans=sum;
	memset(res.a,0,sizeof(res.a));memset(trs.a,0,sizeof(trs.a));
	memset(st.a,0,sizeof(st.a));
	for(int i=0;i<m;i++){
		int cnt=0;
		for(int j=1;j<=m;j++){
			if((j^m)&&!(s[j]^s[j+1])) cnt=(cnt+dfs(i,j,j+1))%MOD;
		}
		if(i) trs.a[k-((m-i+1)>>1)][i]=cnt;
		else st.a[m][1]=cnt;
	}
	for(int i=2;i<m;i++) trs.a[i][i-1]=1;
	if(m>1) st.a[1][1]=1;
	for(int i=m;i<k;i++) trs.a[i+1][i]=1;
	for(int i=1;i<m;i++) trs.a[i][i]=24;
	for(int i=m;i<k;i++) trs.a[i][i]=25;
	for(int i=1;i<=k;i++) res.a[i][i]=1;
	stp=(n+m+1)>>1;
	for(;stp;stp>>=1,trs=trs*trs) if(stp&1) res=res*trs;
	sum=0;for(int i=1;i<=k;i++) sum=(sum+st.a[i][1]*res.a[k][i])%MOD;
	printf("%d\n",(ans-sum+MOD)%MOD);
	return 0;
}