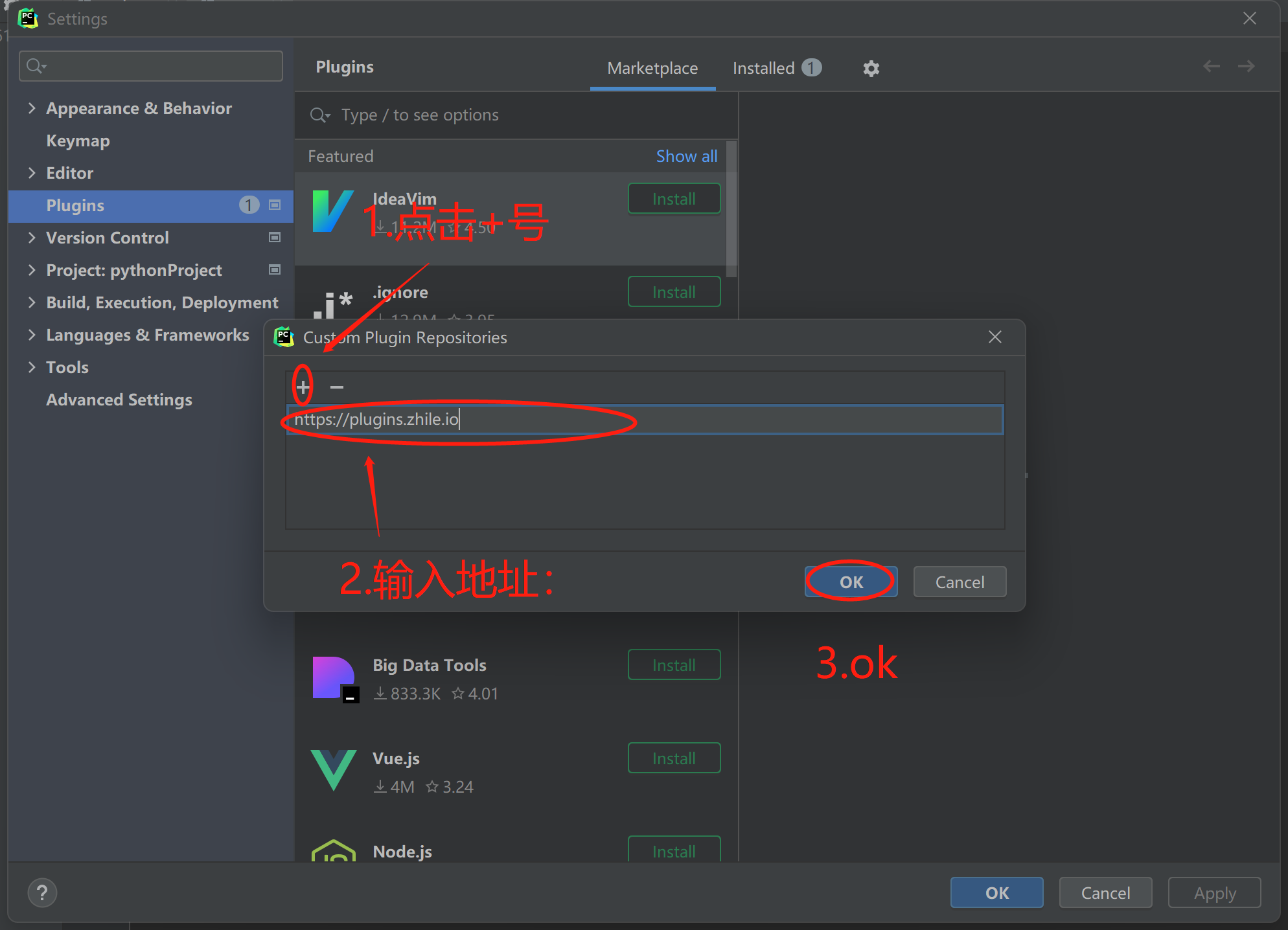
PyCharm破解无限试用
一:安装插件
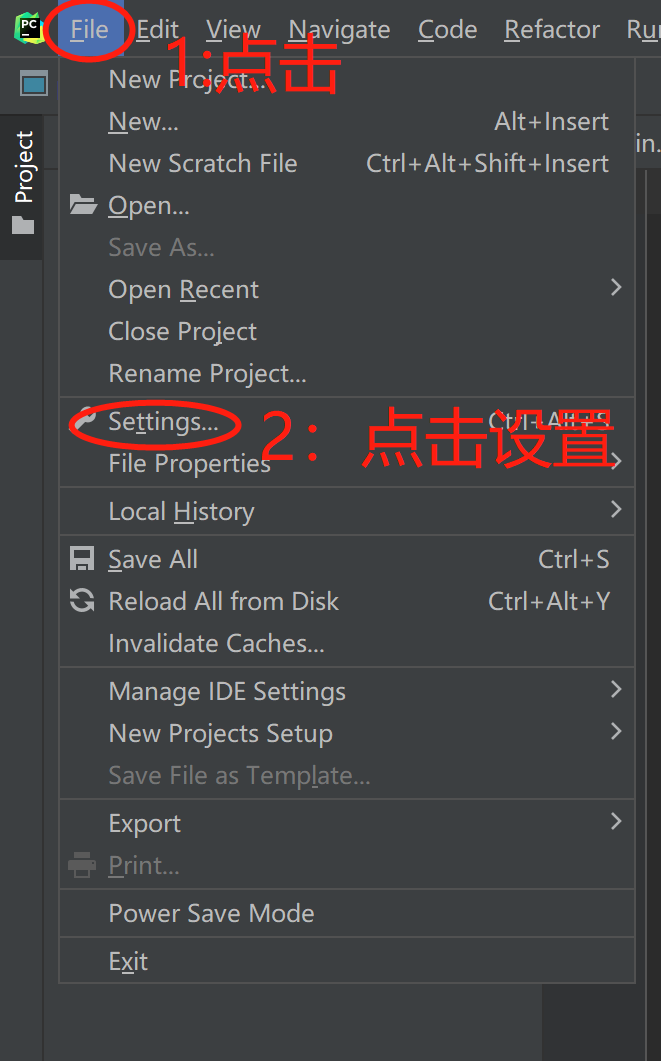
1.打开PyCharm,进入后,点击左上角File,在点击Settings(设置)。
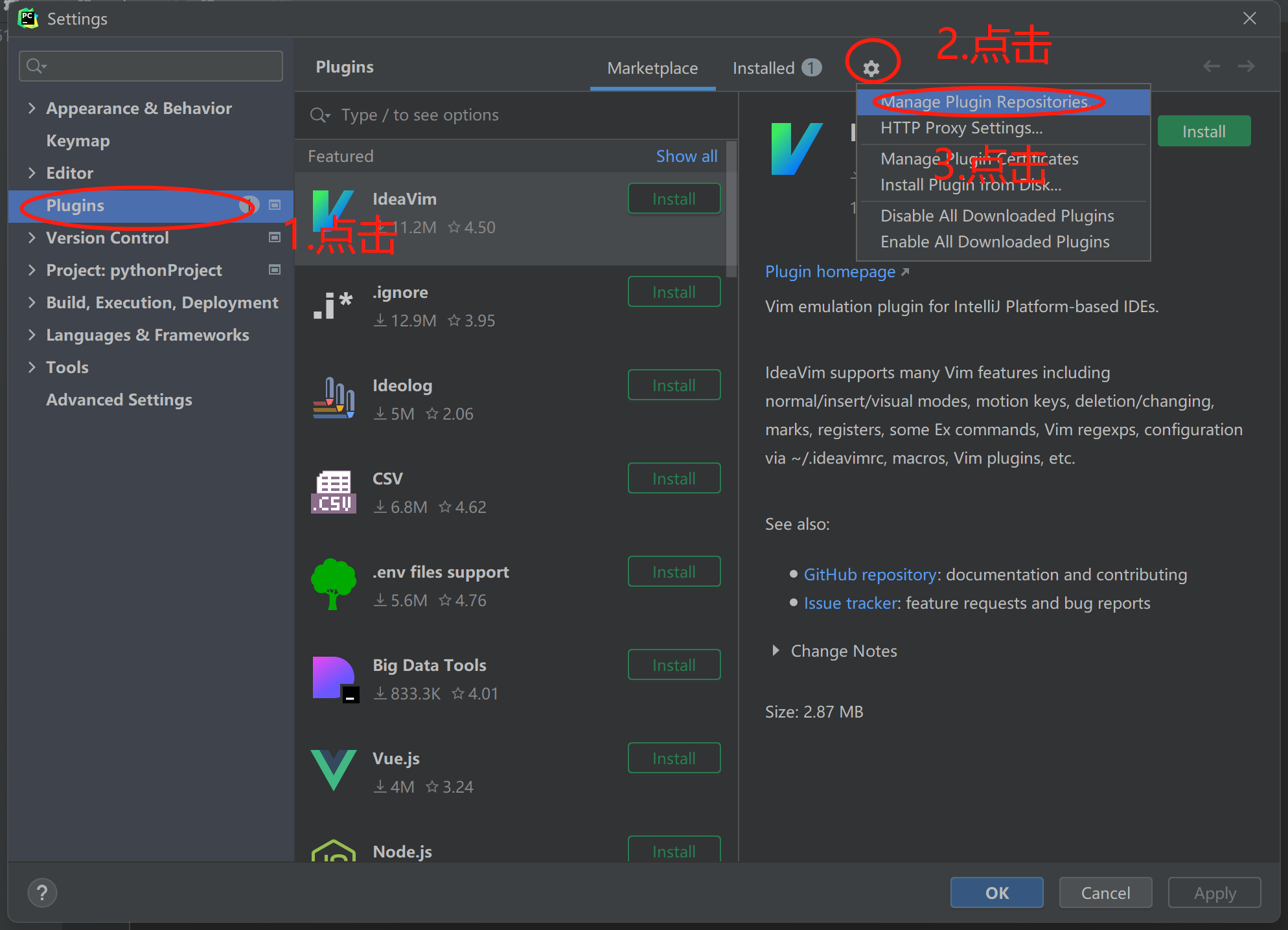
2.进入后,点击Plugins,在点击(2.设置图标),然后点击Manage Plugin Repositories进入。
3.然后,点击+号,添加插件地址:
4.搜索:IDE Eval Reset插件进行安装。如果搜索不到注意是否做好上一步,网络是否流畅,插件会提示安装成功。
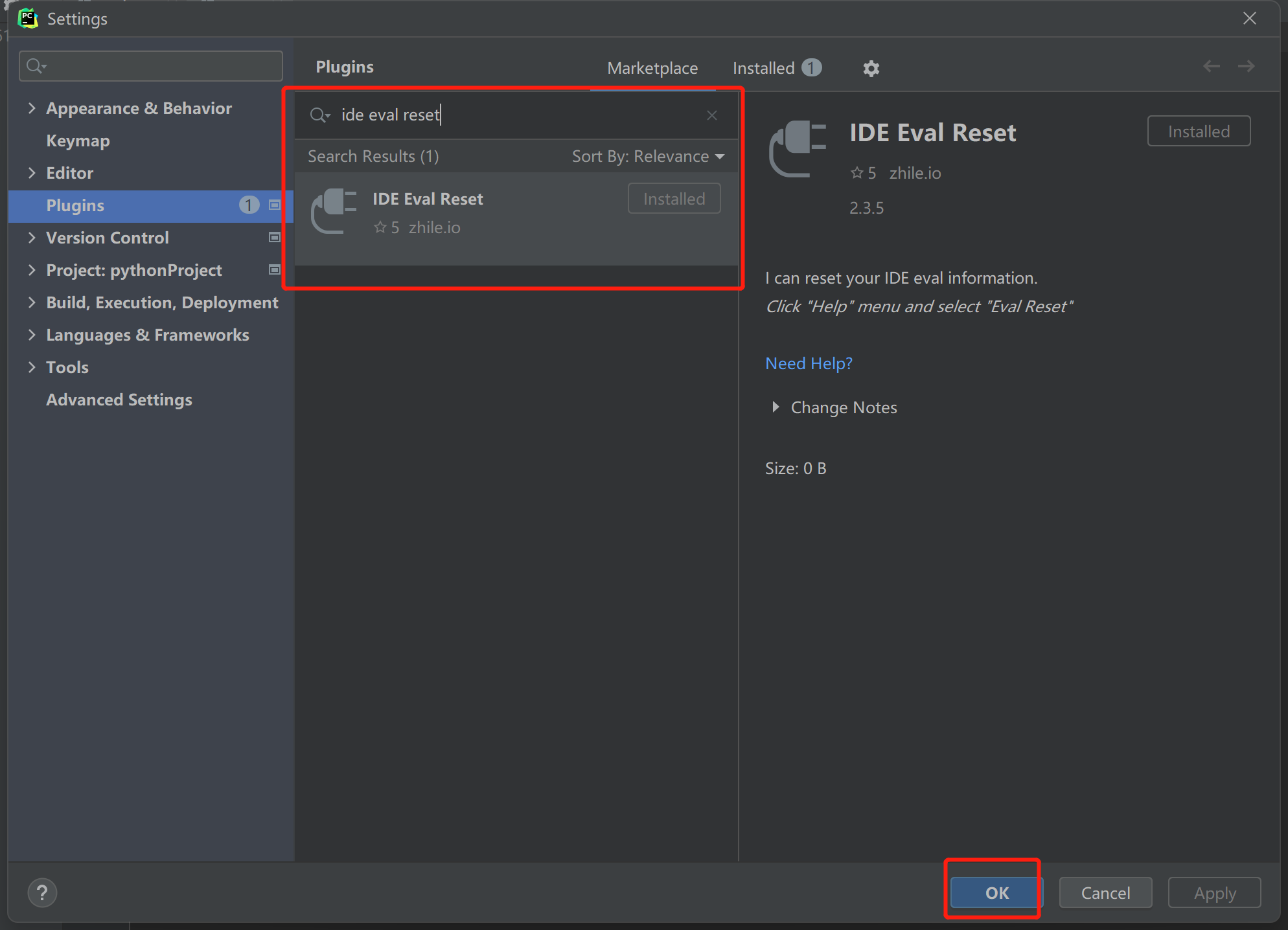
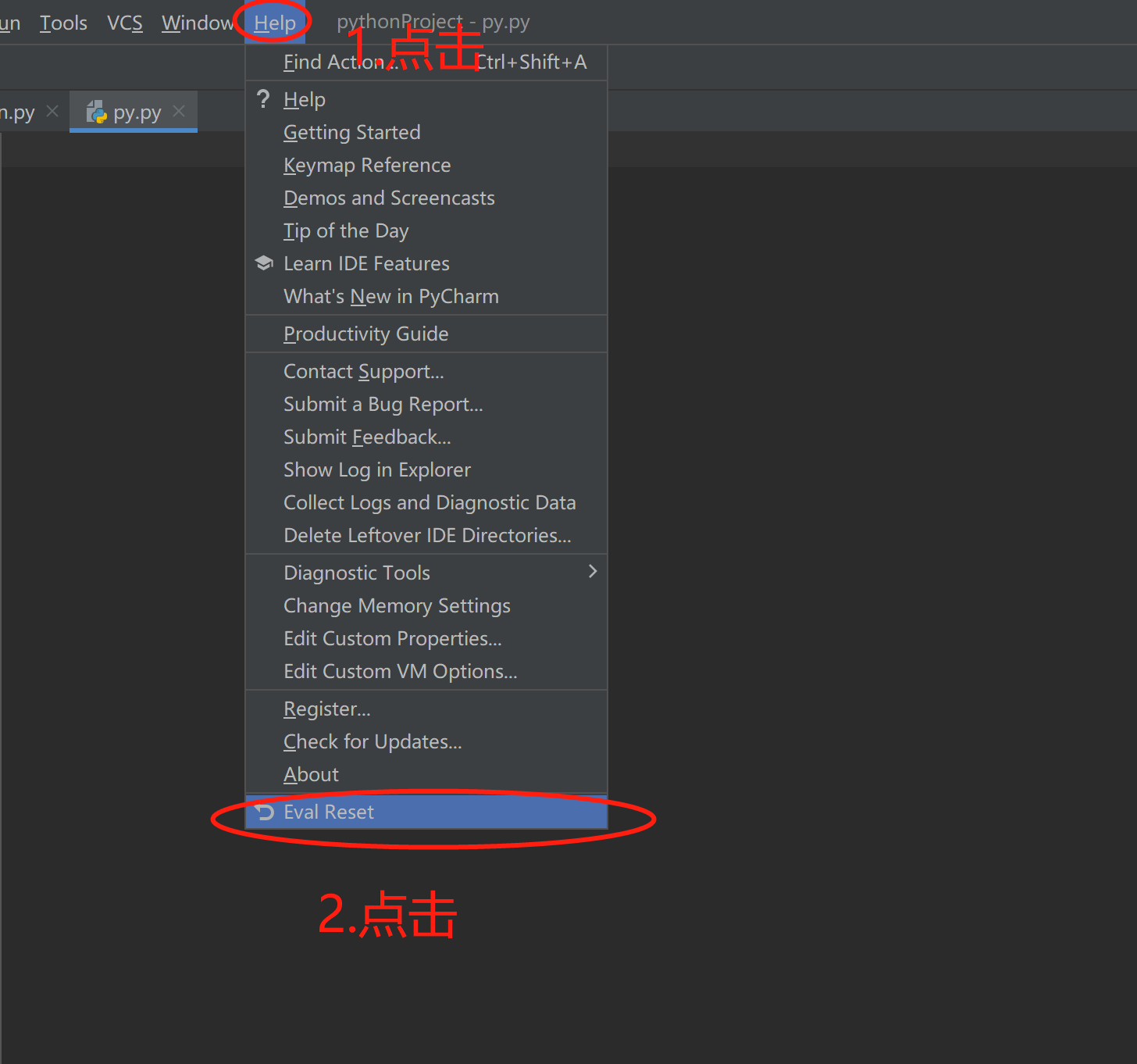
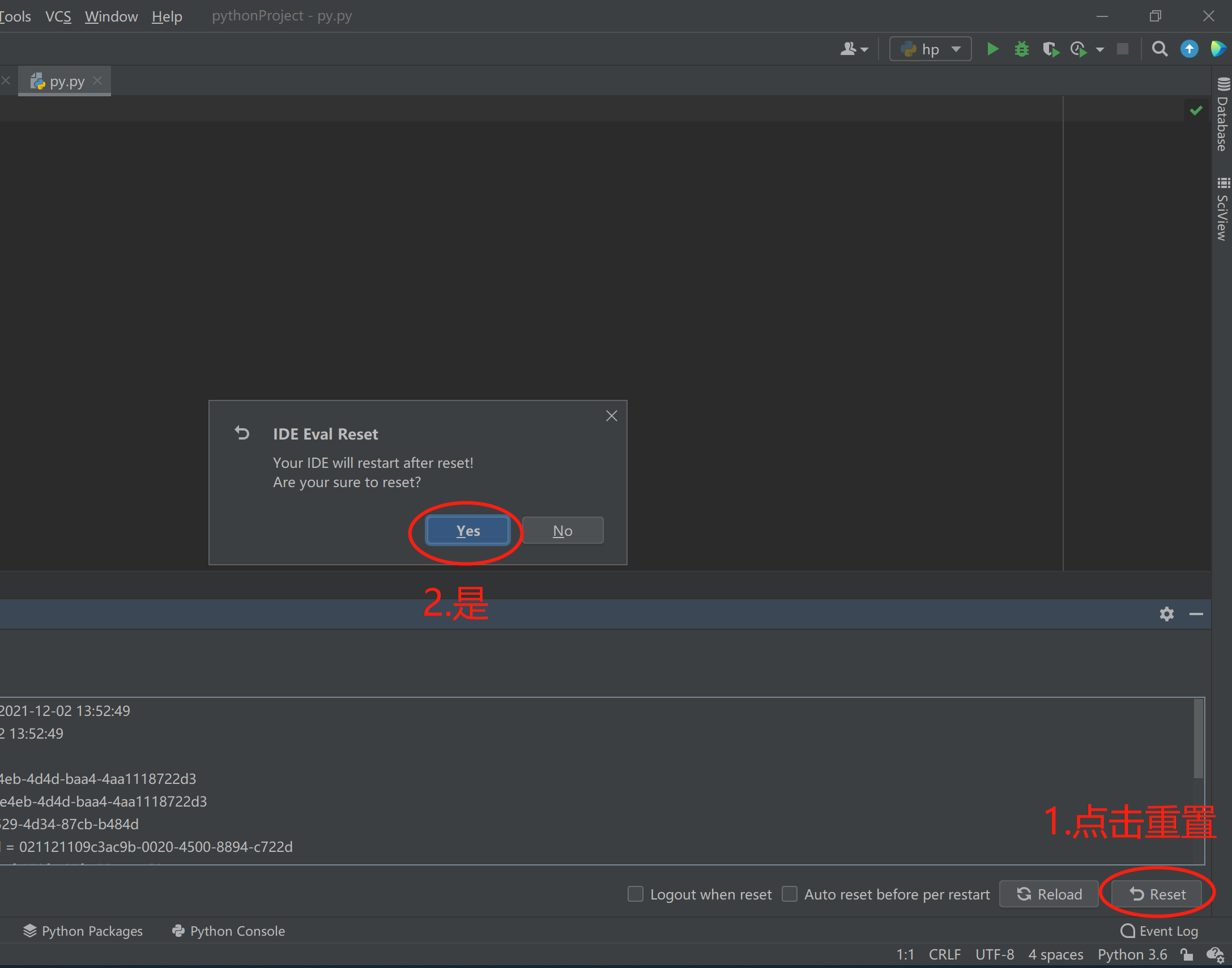
5.在点击Help,点击(2.Eval Reset).重置需要重新启动IDE生效,即可再次获得30天试用期。
PyCharm破解无限试用的更多相关文章
- [海蜘蛛] 海蜘蛛 V8 全线无限试用版 免费发布破解教程
http://bbs.p52.cn/forum.php?mod=viewthread&tid=3499&extra=page%3D1&page=1&_dsign=79c ...
- Pycharm破解版_安装从失败到成功
前言: 入门学习的时候一直用的是社区版的,现在想换个专业版的玩玩. 本文使用的环境说明: win10系统 安装过pycharm社区版,已卸载 已安装python 3.8.5 (建议看完整篇文章后再自行 ...
- Beyond Compare for mac 无限试用方法
1.在官网(http://www.scootersoftware.com/download.php)下载最新的 beyond compare. 2.解压后, 把 beyond compare 复制到应 ...
- 小白学习python第一天,Pycharm破解与用法(持续更新)
目录 Pycharm安装与破解及汉化 Pycharm安装 Pycharm破解 Pycharm汉化 Pycharm使用 添加作者.时间等信息 补充 @ Pycharm安装与破解及汉化 本人最近开始找到了 ...
- JetBrains Pycharm破解,含破解文件和安装包2019.2版
此教程支持最新的2019.3版本的Pycharm,并兼容之前的版本. 一.准备工作: 1.下载Pycharm 有条件的可以自行去官网下载,这里我提供了我下载的版本,已上传到百度网盘,链接在下方. 2. ...
- jetbrains 系列产品无限试用
无限试用插件 在线安装 需要添加第三方插件仓库地址 设置 -- Manage Plugins Reposition... -- + https://plugins.zhile.io plugins 中 ...
- 破解UltraEdit(Ver20.00.0.1040),无限试用
因为是第一次破解较大型的商业软件,所以有必要记录一下,另外UE的价格也实在太贵了... 第零步:准备 准备好破解常用软件.我常用的工具有IDA(用于静态分析).Ollydbg(动态调试).PEiD(用 ...
- 破解Kaleidoscope-2.1.0-134,无限试用
找到超时时间计算的地方,有非常多处,大概几十外,大约类似下面的代码,作者应该是copy了非常多份反复的代码, 10000C592 F2 0F 10 8D 40 FE FF FF ...
- MACOS无限试用Cornerstone的方法
MacOS上Cornerstone用起来还是比较好用的,除了add文件目录时不把底下的文件add上去之外.其实之前用Versions也还可以,奈何太贵,买不起正版,破解版又不好用.Cornerston ...
随机推荐
- 过河(状态压缩,dp)
描述 在河上有一座独木桥,一只青蛙想沿着独木桥从河的一侧跳到另一侧.在桥上有一些石子,青蛙很讨厌踩在这些石子上.由于桥的长度和青蛙一次跳过的距离都是正整数,我们可以把独木桥上青蛙可能到达的点看成数轴上 ...
- 1246 - Colorful Board
1246 - Colorful Board PDF (English) Statistics Forum Time Limit: 2 second(s) Memory Limit: 32 MB ...
- 对XSS的插入的新了解,灵感来自天驿安全
此次针对的是通过Get请求进行插入的XSS语句,或者dom型的xss,也算是了解到的新的插入方式 首先,JavaScript语言中存在拼接性 可以通过代审后闭合前置语句进行self测试是否可以拼接 s ...
- Proximal Algorithms 5 Parallel and Distributed Algorithms
目录 问题的结构 consensus 更为一般的情况 Exchange 问题 Global exchange 更为一般的情况 Allocation Proximal Algorithms 这一节,介绍 ...
- [高数]高数部分-Part II 导数与微分
Part II 导数与微分 回到总目录 Part II 导数与微分 一元函数微分的定义 一元函数定义注意点 基本求导公式 基本求导方法 复合函数求导 隐函数求导 对数求导法 反函数求导 参数方程求导 ...
- [git]初始化项目文件到git分支
将本地和远程仓库关联并push本地项目 1.VCS -> import into Version Control -> Create Git Repository 选择项目文件 2 ...
- Exchange ProxyLogon漏洞分析
Exchange ProxyLogon漏洞分析 前言 续前文继续学习Exchange漏洞 Proxyshell 影响范围 Exchange Server 2019 < 15.02.0792.01 ...
- 通过 v-once 创建低开销的静态组件
<!DOCTYPE html> <html> <head> <meta charset="utf-8"/> <script s ...
- .NET 微服务——CI/CD(4):避坑和一点经验
如果你看过之前几篇文章,应该已经Jenkins成功搭建了CICD环境,但是进入正式环境会有一些坑,不注意中招的话很难受,这里总结一下,避免重复消耗精力. 后门漏洞 Jenkins有后门,这是个老问题了 ...
- Nginx_全局命令设置
刚安装好的Nginx, 命令需要去sbin目录执行,比较麻烦,设置下全局命令,就无需进入nginx的sbin目录执行nginx命令了 1.创建文件 vim /etc/init.d/nginx 把下面代 ...