【论文笔记】Recommendations as Treatments: Debiasing Learning and Evaluation

Recommendations as Treatments: Debiasing Learning and Evaluation

Authors: Tobias Schnabel, Adith Swaminathan, Ashudeep Singh, Navin Chandak, Thorsten Joachims

ICML’16 Cornell University

---

目录

• Recommendations as Treatments: Debiasing Learning and Evaluation
  • 0. 总结
  • 1.研究目标
  • 2.问题背景
  • 3. IPS评价指标
    • 3.1 任务1：评分预测准确率评价
    • 3.2 推荐质量评价
    • 3.3 基于倾向分数的性能评估
    • 3.4 实验验证
  • 4. IPS推荐系统
  • 5. 倾向性评分的估计
  • 6. 实验
    • 6.1 实验设置
    • 6.2 采样偏差对评测指标的影响
    • 6.3 采样偏差对模型训练的影响
    • 6.4 倾向性评分估计准确度的影响
    • 6.5 真实数据集上的性能

0. 总结

本文提出了基于IPS的评测指标和模型训练方法，并提出了两种倾向性评分的估计方法。收集并公开了Coat数据集，在半合成数据集和无偏数据集上，验证了评测指标对Propensity score估计的鲁棒性和IPS-MF的性能优越性。

1.研究目标

去除选择偏差（selection-bias）对模型性能评测（evaluation）和模型训练（training）带来的不利影响。

2.问题背景

推荐系统中的选择偏差（selection bias）可能有两个来源：首先，用户更可能跟自己感兴趣的物品发生交互，不感兴趣的物品更可能没有交互记录；第二，推荐系统在给出推荐列表时也会倾向于给用户推荐符合用户兴趣的产品。

3. IPS评价指标

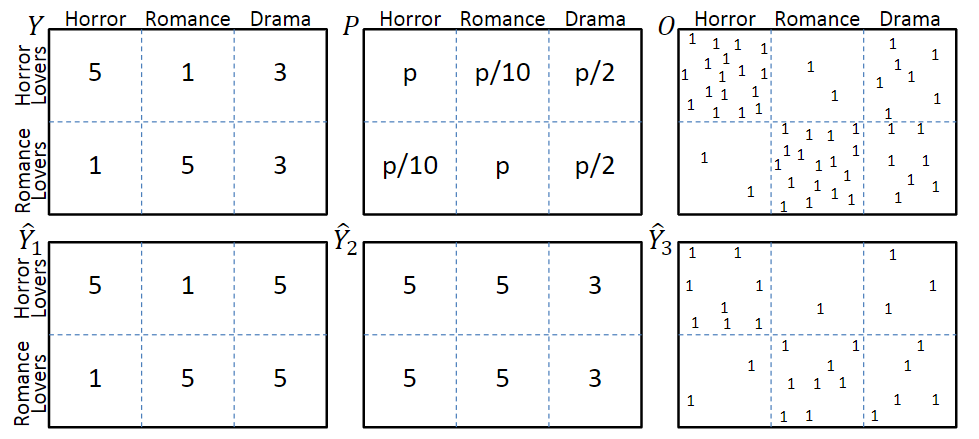
图一

考虑图一中的模型，图中第一行分别表示真实评分Y、曝光概率P和曝光分布O，其中评分越低的交互，观测到的概率也就越低。第二行\(\hat{Y}_1\)和\(\hat{Y}_2\)分别表示两种不同的预测结果，\(\hat{Y}_3\)表示是否发生了交互。

3.1 任务1：评分预测准确率评价

在理想情况下，即所有评分都被观测到时，评价指标为

\[R(\hat{Y})=\frac{1}{U \cdot I} \sum_{u=1}^{U} \sum_{i=1}^{I} \delta_{u, i}(Y, \hat{Y})
\]

但在存在selection bias的场景下，评价指标会变为

\[\hat{R}_{n a i v e}(\hat{Y})=\frac{1}{\left|\left\{(u, i): O_{u, i}=1\right\}\right|} \sum_{(u, i): O_{u, i}=1} \delta_{u, i}(Y, \hat{Y})
\]

从喜恶判断的角度，\(\hat{Y}_1\)明显优于\(\hat{Y}_2\)；但是从评价指标上看，由于\(\hat{Y}_2\)中预测错误的那些交互很少被观测到，因此，\(\hat{Y}_2\)会优于\(\hat{Y}_1\)。

3.2 推荐质量评价

评价推荐结果的质量，也就是在回答一个反事实问题：如果用户与推荐列表中的物品发生交互，而不是实际上的交互历史，用户的体验会得到多大程度的提升？

评价指标可以是DCG等。由于观测数据是有偏的，与3.1中的描述相似，最终的评价指标也是有偏的。

3.3 基于倾向分数的性能评估

解决selection bias的关键在于理解观测数据的生成机制（Assignment Mechanism），包含系统生成（Experimental Setting）和用户选择（Observational Setting）两种因素。

为了解决评测指标的偏差问题，作者提出使用逆倾向分数对观察数据加权，构建一个对理想评测指标的无偏估计器——IPS Estimator：

\[\hat{R}_{I P S}(\hat{Y} | P)=\frac{1}{U \cdot I} \sum_{(u, i): O_{u, i}=1} \frac{\delta_{u, i}(Y, \hat{Y})}{P_{u, i}}\\
\mathbb{E}_{O}\left[\hat{R}_{I P S}(\hat{Y} | P)\right] =\frac{1}{U \cdot I} \sum_{u} \sum_{i} \mathbb{E}_{O_{u, i}}\left[\frac{\delta_{u, i}(Y, \hat{Y})}{P_{u, i}} O_{u, i}\right] \\
=\frac{1}{U \cdot I} \sum_{u} \sum_{i} \delta_{u, i}(Y, \hat{Y})=R(\hat{Y})
\]

其中\(O_{u,i} ~ Bernoulli(P_{u,i})\)，\(P_{u,i}\)为propensity score。

3.4 实验验证

利用MF生成的全曝光模拟数据集，作者设计了几种评分策略，每种策略都有不同的评分错误。基于真实数据集中的曝光情况，计算曝光交互的评价指标，证明了IPS评价指标能有效抵消selection bias带来的评价误差。

4. IPS推荐系统

基于IPS的推荐系统，训练目标为：

\[\underset{V, W, A}{\operatorname{argmin}}\left[\sum_{O_{u, i}=1} \frac{\delta_{u, i}\left(Y, V^{T} W+A\right)}{P_{u, i}}+\lambda\left(\|V\|_{F}^{2}+\|W\|_{F}^{2}\right)\right]
\]

其中\(P_{u,i}\)是倾向性评分，相当于在对应的loss项上加了权重。

5. 倾向性评分的估计

作者提出了两种估计方法

1. 朴素贝叶斯估计

   这个方法似乎是对评分相同的u-i交互给出了相同的评分？

   \[P\left(O_{u, i}=1 \mid Y_{u, i}=r\right)=\frac{P(Y=r \mid O=1) P(O=1)}{P(Y=r)}
   \]

2. 逻辑斯特回归

   将所有关于u-i对的信息都作为特征，来学习一个线性模型

   \[P_{u, i}=\sigma\left(w^{T} X_{u, i}+\beta_{i}+\gamma_{u}\right)
   \]

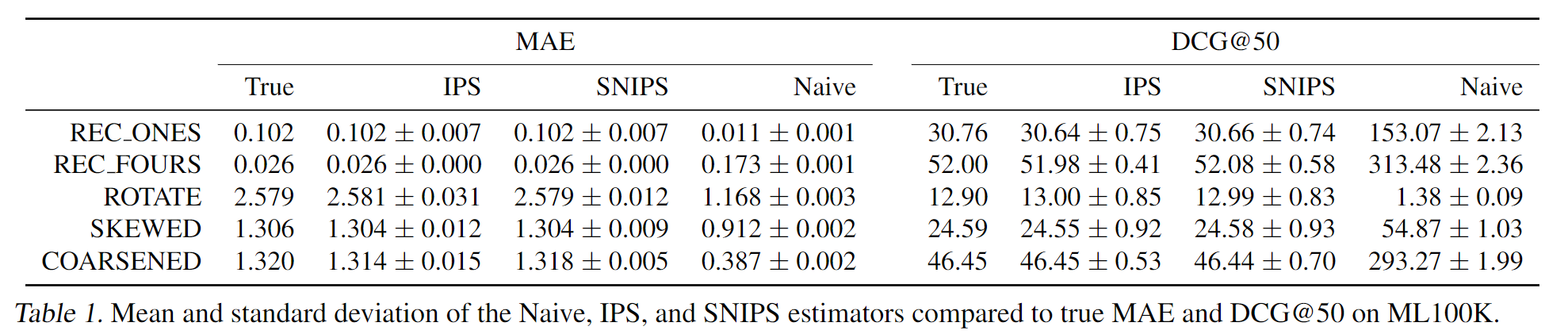
6. 实验

6.1 实验设置

训练集是有偏（MNAR）数据，使用k-折交叉验证来调参，使用无偏数据或者合成的全曝光数据作为测试集。

6.2 采样偏差对评测指标的影响

构建全曝光的合成数据集：在ML 100K数据集上，使用MF 填充所有空缺的评分，并对填充之后的评分分布进行调整，以降低高评分的比例。

实验结果见3.4

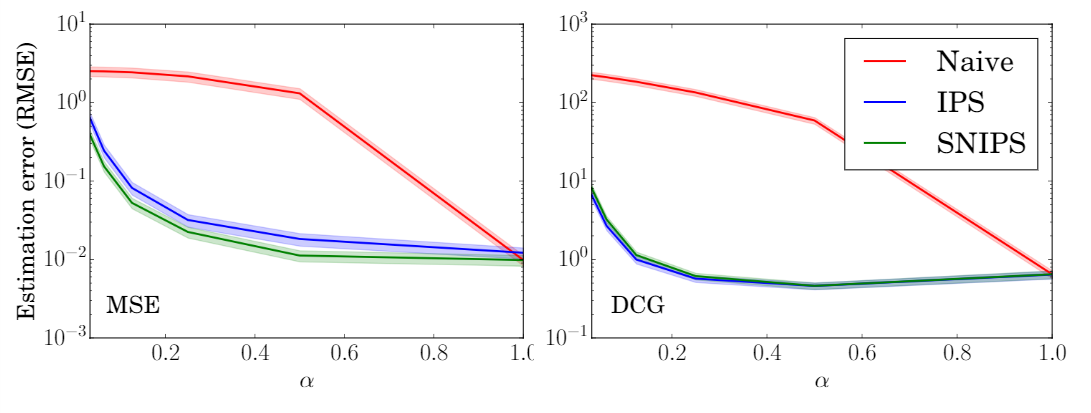
6.3 采样偏差对模型训练的影响

对于不同程度的选择偏差（\(\alpha\)越小，选择偏差越大)，实验结果如下图。

可见，IPS-MF和SNIPS-MF的性能要明显优于naive-MF。

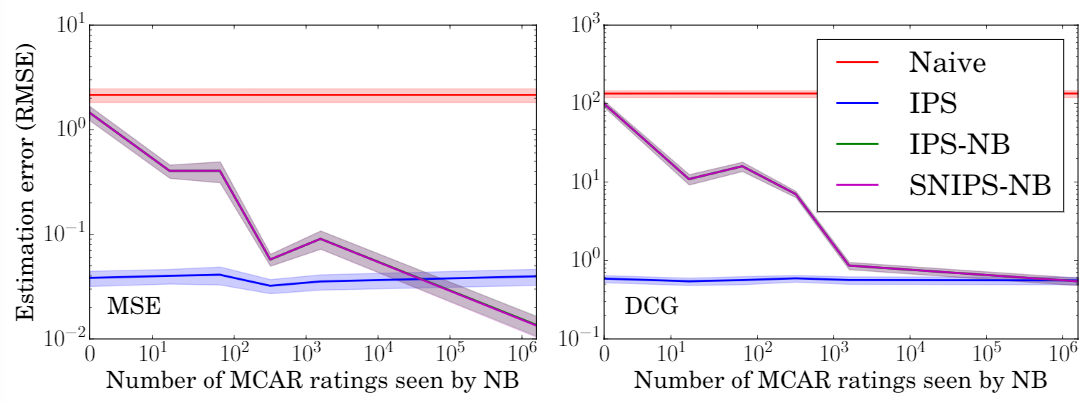
6.4 倾向性评分估计准确度的影响

使用不同比例的数据来估计倾向性评分，可以看出，在所有条件下，IPS和SNIPS都优于MF，验证了模型对倾向性评分的鲁棒性。

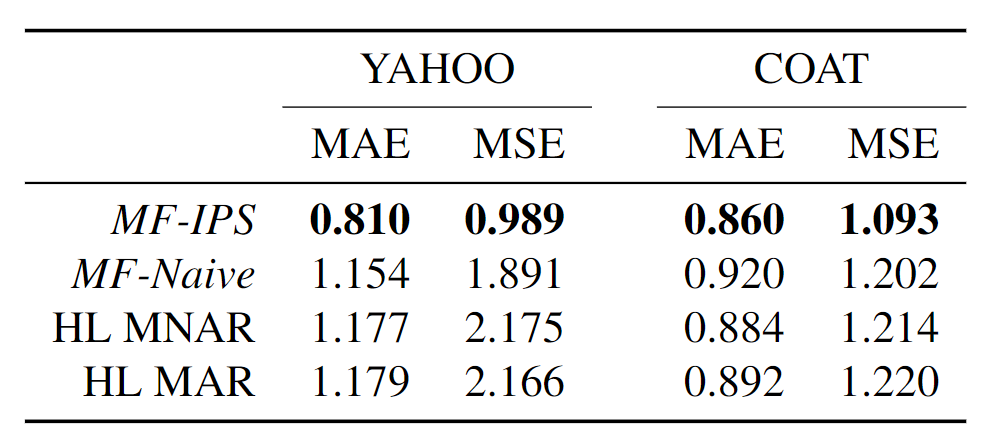
6.5 真实数据集上的性能

Yahoo! R3：使用5%的无偏数据来估计倾向性评分，95%的无偏数据作为测试集。

Coat：本文收集了一个新的无偏数据集Coat（很大的贡献），包含290个user和300个item，每个user自主选择24个商品给出评分，并对16个随机商品给出评分（1-5分）。

实验结果表明，在两个数据集上都优于最好的baseline。