【BZOJ2654】tree(生成树 二分)

题目链接

大意

给你一个无向带权连通图，每条边是黑色或白色，求一棵最小权的恰好有\(Need\)条白色边的生成树。

题目保证有解，输出最小权值。

其中每条边权在\([1,100]\)范围内。

思路

首先有一个比较明显的想法：

用Kruskal跑出一个最小生成树，然后再不断往其中加边调整白色边的数量，用LCT维护圈内最大异色边。

好吧，这种极其复杂的算法可以被以下例子卡掉。

假如随便跑的一个最小生成树是下图：

（边左边为颜色，右边为边权）



再考虑加入以下边：



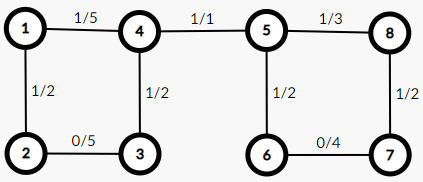
假如需要一条白边，并且按从小到大的顺序选白边，那么就会先选 6-7 这条边，删 5-8 这条边，这样做会产生 1 的贡献。但如果我们选 2-3 这条边，删 1-4 这条边，那么对答案的贡献就是 0，明显更优。

---

考虑一个正常的算法：

我们考虑给每条白边附加一个权值\(W\)，使得白边边权由\(Val\)变为\(Val+W\)，然后再跑一遍最小生成树。

可以发现，当\(W\)越大时，白边数量越少，即呈单调性。

于是考虑二分\(W\)的值，每次二分根据当前最小生成树能得到的最小或最大白边数与\(Need\)的大小关系Check就行。

正确性小记：

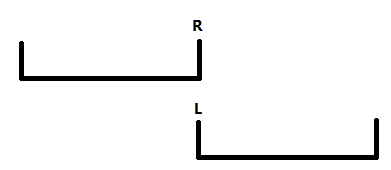
• 对于相邻的两个\(W\)值，倘若存在它们的可选白边数量区间正好不等（即无交集），而\(Need\)又正好在它们中间的情况，那么此时就会出问题（无法二分到正确解）。
• 但其实这种情况并不会出现，设两个区间的空隙为\(D(D\ge 2)\)，那么就会有至少\(D\)条白边在刚才的+1中，变得比原位上的黑边大1，设原位上的黑边数量为\(X(X\ge 1)\)。
  
  
• 设左边那个区间的右端点为\(R\)（如图），那么在算\(L\)的情况时，那\(X\)条黑边的优先级就会比\(D\)条白边的优先级高；同时，在算\(R\)的情况下也是如此。故在算\(L\)与\(R\)时，Kruskal算法中边的顺序是一样的，即相邻两个区间是会重着端点的，即\(D=0\)，即不存在\(Need\)不被任意一个区间包含的情况。
  
  

细节：

• 二分取值与最小生成树所取最小最大白边数的关系：
  
  由于对于同一个\(W\)，可能会有多种选白边数量的方法而生成相同权值的最小生成树的情况，即白边可选数量实际上是一段区间，所以我们需要考虑是取该区间的左端点还是右端点。
• 倘若是从下界逼近，即\(Ans\)选取\(L\)时，那么应取最小白边数量，这样\(L\)才会在 \(Mid\)正好为答案且\(Mid\)的白边数量区间跨越了\(Need\) 的情况下合法（\(R\)不会占\(L\)的位置）。
• 同理，\(Ans\)选取\(R\)时，应取最大白边数量。

TLE小记：

• 时间复杂度为\(O(N*log(N)*log(W))\)，其中\(log(W)\)决定着代码的命运。

代码

#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN=100005;
int N,M,Ned,Fa[MAXN];long long Ans;
struct Edge{int x,y,col,vis,id,z;}s[MAXN],tmp[MAXN];
bool cmp(Edge A,Edge B){return A.z<B.z||(A.z==B.z&&A.col<B.col);}
int Find(int x){return Fa[x]==x?x:Fa[x]=Find(Fa[x]);}
void Turn(double p){
	for(int i=1;i<=M;i++){
		s[i]=tmp[i];
		if(tmp[i].col==0)s[i].z+=p;
	}sort(s+1,s+M+1,cmp);
}
int Get(){
	int ret=0;
	for(int i=1;i<=N;i++)Fa[i]=i;
	for(int i=1;i<=M;i++){
		int x=Find(s[i].x),y=Find(s[i].y);
		if(x==y)continue;Fa[x]=y;
		if(s[i].col==0)ret++;
		s[i].vis=1;
	}
	return ret;
}
bool Check(int p){
	Turn(p);return Get()<=Ned;
}
int main(){
	scanf("%d%d%d",&N,&M,&Ned);
	for(int i=1,col;i<=M;i++)
		scanf("%d%d%d%d",&tmp[i].x,&tmp[i].y,&tmp[i].z,&tmp[i].col),tmp[i].x++,tmp[i].y++,tmp[i].id=i;
	double L=-101,R=101;
	while(L+1<R){
		double mid=(L+R)/2;
		if(Check(mid))R=mid;
		else L=mid;
	}
	Turn(L);Get();Ans=0;
	for(int i=1;i<=M;i++)
		if(s[i].vis)Ans+=tmp[s[i].id].z;
	printf("%lld\n",Ans);
}