C++实现二叉树的链接存储结构（先根、中根和后根遍历）

验证二叉树的链接存储结构及其上的基本操作。

[实验要求]：
1. 从文件创建一棵二叉树，并对其初始化；
2. 先根、中根、后根遍历二叉树；
3. 在二叉树中搜索给定结点的父结点；
4. 搜索二叉树中符合数据域条件的结点；
5. 从二叉树中删除给定结点及其左右子树。

[截图]：
1. 文件截图

2. 操作截图

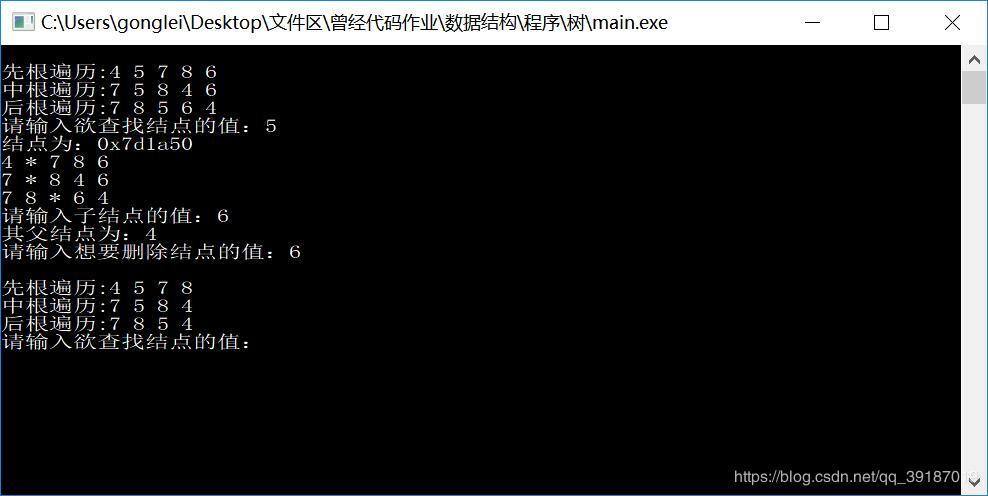
[实现代码]：
分成三个文件tree.h、tree.cpp和main.cpp

tree.h:

#ifndef _TREE_H
#define _TREE_H
#include<iostream>
#include<fstream>
using namespace std;
class Node{
 private:
  Node *right;
  Node *left;
 public:
  char data;
  Node(const char&item,Node*lptr=NULL,Node*rptr=NULL):data(item),left(lptr),right(rptr){}
  Node*getleft(void)const{return left;}
        void setleft(Node*L){left=L;}
        Node*getright(void)const{return right;}
        void setright(Node*R){right=R;}
        char&getdata(){return data;}
        void setdata(const char&item){data=item;}
};
class tree{
 private:
  Node *root;
  char stop;
 public:
  tree(Node*t=NULL):root(t){}
  ~tree(){delete root;}
  void createtree();
  Node*create(char*a);
     Node*getroot(){return root;}
     void setstop(char stop) {this->stop=stop;}
     Node*father(Node*root,Node*son);
     Node*find(Node*root,const char&item)const;
     void preorder(Node*root)const;
     void inorder(Node*root)const;
     void postorder(Node*root)const;
     void levelorder(Node*root)const;
     void deletesth(Node*t);
};
#endif

tree.cpp:
createtree函数中有打开文件操作记得修改

#include<iostream>
#include<fstream>
#include<cstdlib>
#include"tree.h"
using namespace std;
char stop=;
int ii=;
int xx=;
Node*tree::create(char *a){
 Node*root, *root1, *root2;
    char userInput;
    userInput=a[xx];
    xx++;
    if(userInput==stop){
        root=NULL;
        return root;
    }
    else{
     root=new Node(userInput,NULL,NULL);
     if(!root)
     return NULL;
     root1=create(a);
     root->setleft(root1);  //设置左子树
  root2=create(a);
     root->setright(root2);     //设置右子树
     return root;
 }
}
void tree::createtree(){
    char userStop;
    char a[];
    ifstream file("tree.txt");
    if(!file.is_open()){
     cout<<"文件打开失败！"<<endl;
     exit();
 }
 file>>userStop;
    setstop(userStop);
 while(!file.eof()){
  file>>a[ii];
  ii++;
 }
    root=create(a);
}
Node*tree::father(Node*root,Node*son){
    Node*temp;
    if(root==NULL||son==NULL)
        return NULL;
    if(root->getleft()==son||root->getright()==son)
        return root;
    temp=father(root->getleft(),son);
    if(temp!=NULL)
        return temp;
    else
        return father(root->getright(),son);
}
Node*tree::find(Node * root,const char& item)const{
    Node*temp;
    if(root==NULL)
        return NULL;
    if(root->getdata()==item)
        return root;
    temp=find(root->getleft(),item);
    if(temp!=NULL)
        return temp;
    else
        return find(root->getright(),item);
}
void tree::preorder(Node*root)const{
    if(root!=NULL) {
        cout<<root->getdata()<<" ";
        preorder(root->getleft());
        preorder(root->getright());
    }
}
void tree::inorder(Node*root)const {
    if(root != NULL) {
        inorder(root->getleft());
        cout<<root->getdata()<<" ";
        inorder(root->getright());
    }
}
void tree::postorder(Node*root)const{
    if(root!=NULL){
        postorder(root->getleft());
        postorder(root->getright());
        cout<<root->getdata()<<" ";
    }
}
void tree::deletesth(Node*t){
 if(t==NULL)return;
 if(t==root){
  delete(t);
  root=NULL;
  return;
 }
 Node*p,*q;
 p=t;
 q=father(root,p);
 if(q){
  if((q->getleft())==p)q->setleft(NULL);
  if((q->getright())==p)q->setright(NULL);
 }
 delete(p);
}

main.cpp:

#include<iostream>
#include<fstream>
#include"tree.h"
#include"tree.cpp"
using namespace std;
int main(){
 char Input;
    tree b2,bt;
    Node*father;
    Node*temp;
 b2.createtree();
 while(){
    cout<<endl<<"先根遍历:";
 b2.preorder(b2.getroot());
    cout<<endl<<"中根遍历:";
 b2.inorder(b2.getroot());
    cout<<endl<<"后根遍历:";
 b2.postorder(b2.getroot());
    cout<<endl<<"请输入欲查找结点的值：";
    cin>>Input;
    temp=b2.find(b2.getroot(),Input);
    if(temp==NULL){
        cout<<"无该结点！！！"<<endl;
    }
 else{
  cout<<"结点为："<<temp<<endl;
        temp->data='*';
        b2.preorder(b2.getroot());
        cout<<endl;
        b2.inorder(b2.getroot());
        cout<<endl;
        b2.postorder(b2.getroot());
        cout<<endl;
        temp->data=Input;
    }
    cout<<"请输入子结点的值：";
    cin>>Input;
    temp=b2.find(b2.getroot(),Input);
    father=b2.father(b2.getroot(),temp);
    if(father==NULL) {
        cout<<"无该结点！！！"<<endl;
    }
 else{
        cout<<"其父结点为："<<father->getdata()<<endl;
    }
    cout<<"请输入想要删除结点的值：";
 cin>>Input;
 temp=b2.find(b2.getroot(),Input);
 b2.deletesth(temp);}
    return ;
}