tarjan 复习笔记 割点与桥

定义分析

• 给定一个无向连通图\(G=(V,E)\)

• 对于\(x\in Y\),如果删去\(x\)及与\(x\)相连的边后，\(G\)分裂为两个或者两个以上的不连通子图，那么称\(x\)为\(G\)的割点

• 对于\((x,y)\in E\),如果删去\((x,y)\)后，\(G\)分裂为两个不连通的子图，那么就称\(（x,y）\)为\(G\)的桥或者割边

• 一般无向图（不保证连通）的割点和桥 指的是各个连通块的割点和桥

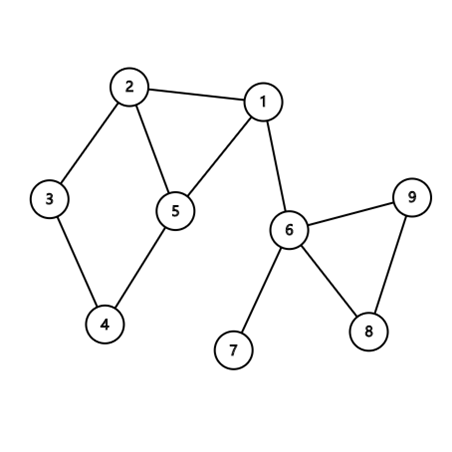
在这个图中，\(1,6\)号结点为割点，\(（1,6），（6,7）\)是桥

概念引入(Tarjan独特概念)

• 时间戳：对一张无向连通图进行DFS，使每个点只经过一遍，并且按照每个点第一次被访问的时间顺序依次标号（也就是他们的DFS序），这个标号被称为时间戳，记为\(dfs_x\).

• 搜索树：在时间戳形成的DFS过程中，我们发现所有构成递归的边构成了一棵树，称之为无向连通图的搜索树.

• 追溯值：设\(subtree(x)\)表示搜索树中以\(x\)为根的子树，节点\(u\)的追溯值我们定义为\(low_u\)，定义为一下结点时间戳的最小值.
  
  1、位于\(subtree(x)\)中的节点.
  
  2、通过一条不在搜索树上的边，可以到达\(subtree(x)\)的节点.

构建方法（追溯值，时间戳）

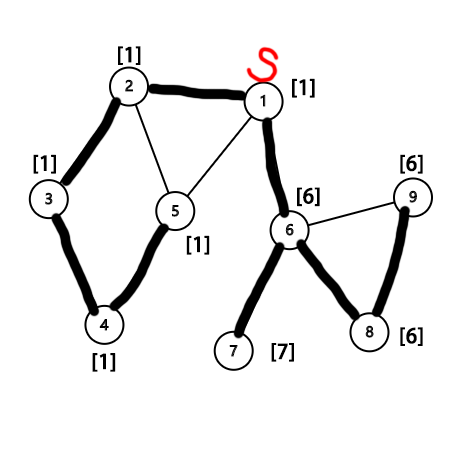
• 第一次访问到一个节点\(x\)的时候，首先我们令\(low_x=dfn_x\).

• 然后，我们继续考虑与\(x\)相邻的每一条边，如果没有被访问过，那么就递归
  
  地却访问他们，回溯是更新\(low_x\).

• 如果\(y\in subtree(x)\)，那么\(low_x=min(low_x,low_y)\).

• 否则\(low_x=min(low_x,dfn_y)\).

割点的判定

• 如果\(x\)不是搜索树上的根节点，那么\(x\)的割点判定条件为当且仅当搜索树上的一个子节点\(y\)满足

\[dfn_x\leq low_y
\]

• 解释：（请先理解好追溯值定义）这个公式表示的意思是在\(subtree(y)\)中的点如果不经过\(x\)那么就无法到达比\(x\)更早访问过的点。

• 特殊情况:如果\(x是根节点\)，那么\(x\)是割点当且仅当搜索树上的两个子节点\(y\)满足上述条件时成立，表示这两个子节点无法互相到达

桥的判定

• 无向边\(（x,y）\)是桥，当且仅当\((x,y)\),位于搜索树上，并且在搜索树上\(x\)的一个子节点\(y\)满足

\[dfn_x<low_y
\]

• 表示从\(subtree(y)\)出发，在不经过\((x,y)\)的前提下，无论是怎么走都无法到达\(x\)或者比\(x\)更早访问过的节点

• 当然，一个简单环里面的边一定不是桥，因为他是圈圈！！！

• 不在搜索树上的边至少都位于至少一个环中，因为不在搜索树上的边那么就表示它一定是连接到了已经被搜索过的点，所以当通过那个点的时候一定能在回到它本身，所以一定在至少一个环中

割点,桥判定代码

#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<map>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=1e5+9;
struct node{
	int last;
	int to;
}e[N*2];
int head[N],vis[N],dfn[N],low[N],cut[N],cnt,poi,tot;
int n,m,root;
void add(int from,int to)
{
	e[++cnt].last=head[from];
	e[cnt].to=to;
	head[from]=cnt;
}
void tarjan(int x)
{
	dfn[x]=low[x]=++poi;
	int flag=0;//根节点的判断
	for(int i=head[x];i;i=e[i].last)
	{
		int v=e[i].to;
		if(!dfn[v])//没有打时间戳说明未被搜索到过
		{
			tarjan(v);
			low[x]=min(low[v],low[x]);
			if(low[v]>=dfn[x])
			{
				flag++;
				if(x!=root||flag>1)
				{
					cut[x]=1;
				}
			}
		}
		else low[x]=min(low[x],dfn[v]);
	}
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int x,y;
		cin>>x>>y;
		if(x==y) continue;
		add(x,y);
		add(y,x);
	}
	for(int i=1;i<=n;i++)
	{
		if(!dfn[i])
		{
			root=i;
			tarjan(i);
		}
	}
	for(int i=1;i<=n;i++)
	{
		if(cut[i]) tot++;
	}
	cout<<tot<<endl;
	for(int i=1;i<=n;i++)
	{
		if(cut[i]) cout<<i<<" "; //输出割点
	}
	return 0;
}```

```void tarjan(int x, int in_edge) //求桥
{
	dfn[x] = low[x] = ++num;
	for (int i = head[x]; i; i = Next[i]) {
		int y = ver[i];
		if (!dfn[y]) {
			tarjan(y, i);
			low[x] = min(low[x], low[y]);
			if (low[y] > dfn[x])
				bridge[i] = bridge[i ^ 1] = true;
		}
		else if (i != (in_edge ^ 1))
			low[x] = min(low[x], dfn[y]);
	}
}