树形dp 之 小胖守皇宫

题目描述

huyichen世子事件后，xuzhenyi成了皇上特聘的御前一品侍卫。

皇宫以午门为起点，直到后宫嫔妃们的寝宫，呈一棵树的形状；有边相连的宫殿间可以互相望见。大内保卫森严，三步一岗，五步一哨，每个宫殿都要有人全天候看守，在不同的宫殿安排看守所需的费用不同。

可是xuzhenyi手上的经费不足，无论如何也没法在每个宫殿都安置留守侍卫。

帮助xuzhenyi布置侍卫，在看守全部宫殿的前提下，使得花费的经费最少。

输入输出格式

输入格式

输入文件中数据表示一棵树，描述如下：

第1行\(n\)，表示树中结点的数目。

第2行至第\(n+1\)行，每行描述每个宫殿结点信息，依次为：该宫殿结点标号\(i(0<i<=n)\)，在该宫殿安置侍卫所需的经费\(k\)，该边的儿子数\(m\)，接下来\(m\)个数，分别是这个节点的\(m\)个儿子的标号\(r_1,r_2,...,r_m\)。

对于一个\(n(0 < n <= 1500)\)个结点的树，结点标号在\(1\)到\(n\)之间，且标号不重复。

输出格式

输出文件仅包含一个数，为所求的最少的经费。

样例

样例输入

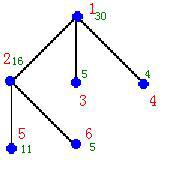
6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0

样例输出

25

题解

当我们分析一个节点的时候，很容易想到起码有两种情况：在这个节点设侍卫或者不设。但是如果单纯地只是分析它不设，那么依据题意，它必须得被观测到，那么它的子节点到底要不要设呢？此时便又要分两种情况：被儿子观测或是被父亲观测。因此到这里我们把这个题已经抽象成了三种状态转移：

• \(f[i][1]\)表示在\(i\)节点的子节点设一个侍卫的最小经费（默认\(i\)节点自己不设）

• \(f[i][2]\)表示在\(i\)节点设一个侍卫的最小经费

• \(f[i][3]\)表示在\(i\)节点的父节点设一个侍卫的最小经费（默认\(i\)节点自己不设）

• 1、\(f[i][1]\)表示i节点被它的子节点观测到，这时我们就要考虑：是不是子节点一定会再自己那里设一个观测点呢？当然不一定了，当且仅当子节点 \(f[son[i]][2]<f[son[i]][1]\)时，他才会在自己那里设。那么我们就需要找遍i的所有儿子，只要有一个儿子可以设就行了。这个怎么实现呢？我们只需先把所有儿子的\(min(f[v][1],f[v][2])\)累加到\(f[i][1]\)上，再取所有儿子的\(f[v][2]-min(f[v][1],f[v][2])\)最小值\(t\)，如果这个最小值\(t\)不是0，就说明没有一个儿子打算在自己那里设点，就必须强迫一个儿子改变最优解，来满足i节点的需求，即用\(f[i][2]\)加上\(t\)，若\(t\)是0，不影响，加上也无妨。

f[i][1]+=min(f[v][1],f[v][2]);//既然默认自己不会设点，就不可能有f[v][3]这个状态
f[i][1]+=t;

• 2、\(f [ i ] [ 2 ]\) 表示\(i\)节点自己那里设了一个侍卫，既然自己已经设了一个，那么子节点的三种情况都要考虑。

f[i][2]+=min(f[v][1],f[v][2],f[v][3]);

• 3、\(f [ i ] [ 3 ]\) 表示\(i\)节点被它的父节点观测到，那么除了\(f [ v ] [ 3 ]\)要被排除掉，其他的只要保证子节点可以被观测到即可。

f[i][3]+=min(f[v][1],f[v][2]);

代码

下面是参考代码：

#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn=1500+50,
          INF=0x3f3f3f3f;
vector<int> son_id[maxn];
int f[maxn][4],//树形dp : 1=>son 2=>itself 3=>father
    cnt[maxn],//出现次数
    son_num[maxn],//儿子数目
    cost[maxn];//所需的经费
int n;
void tree_dp(int x){
    int ans=INF;
    for(int i=0;i<son_num[x];i++){
        int son=son_id[x][i];
        tree_dp(son);
        f[x][1]+=min(f[son][1],f[son][2]);
        ans=min(ans,f[son][2]-min(f[son][1],f[son][2]));
        f[x][2]+=min(f[son][1],min(f[son][2],f[son][3]));
        f[x][3]+=min(f[son][1],f[son][2]);
    }
    f[x][1]+=ans;
    f[x][2]+=cost[x];
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        int id;
        cin>>id;
        cin>>cost[id]>>son_num[id];
        for(int j=1;j<=son_num[id];j++){
            int x;cin>>x;
            cnt[x]++;
            son_id[id].push_back(x);
        }
    }
    for(int i=1;i<=n;i++)
        if(cnt[i]==0){
            tree_dp(i);
            cout<<min(f[i][1],f[i][2]);
        }
    return 0;
}