关于PCA主成分分析的一点理解

PCA 即主成分分析技术，旨在利用降维的思想，把多指标转化为少数几个综合指标。

假设目前我们的数据特征为3，即数据维度为三，现在我们想将数据降维为二维，一维：

我们之前的数据其实就是三维空间中的一个个点，这些点漫布在空间中，如下图所示

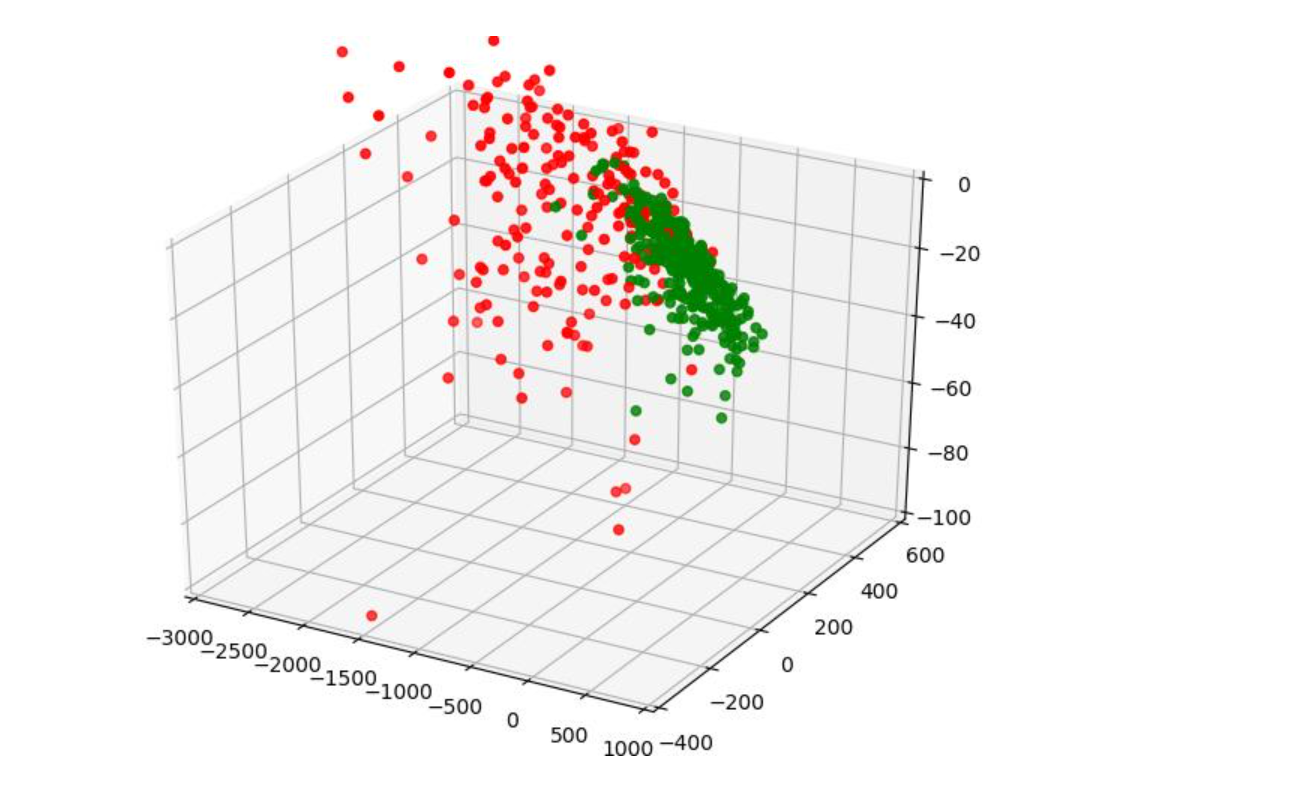
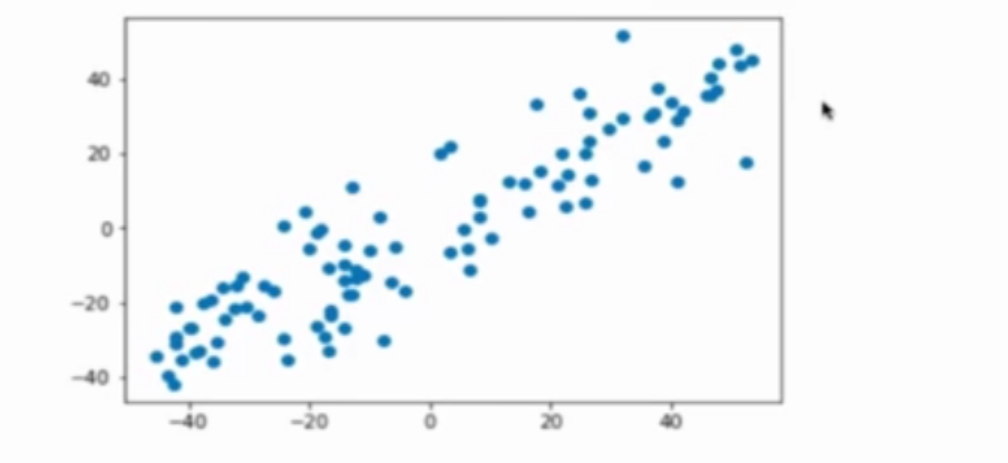
将这些数据去掉一个维度，也就是说将这些数据映射到某一个平面上，可以是xy平面，可以是xz平面，也可以是yz平面。

条件是映射后的数据的方差要保持最大，保留最大的数据波动性，也就是保留最多的原始的数据量。

在此基础上如果还要继续进行PCA，也就是将二维空间中的点映射到一维的线上（正确的方向应该为倾斜向上）

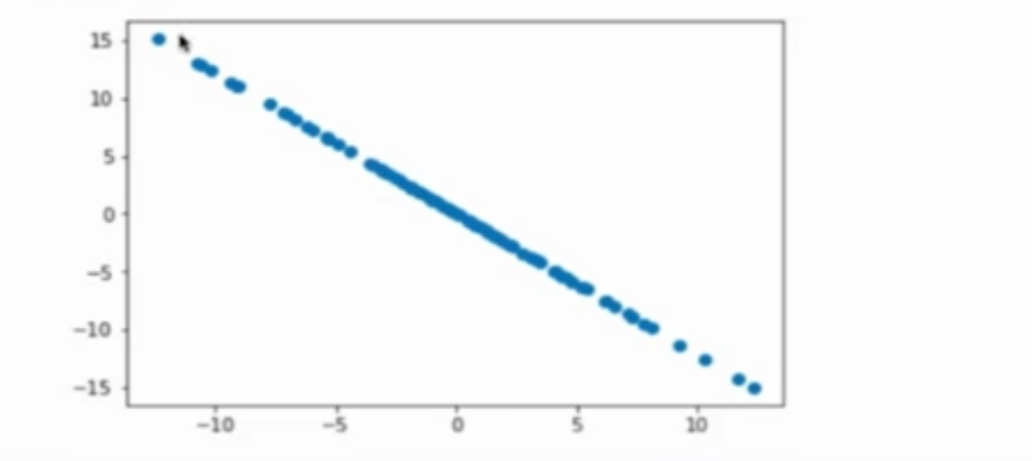
所选择的这条线条件也是要保持数据间的方差最大

因此该问题就转化为求数据方差的极大值问题，我们可以将极大值问题转化为极小值问题，然后通过梯度下降法求出极值点。

进而求出这个面的方向，这条线的方向。