Image Processing and Analysis_8_Edge Detection：Edge Detection Revisited ——2004

此主要讨论图像处理与分析。虽然计算机视觉部分的有些内容比如特 征提取等也可以归结到图像分析中来，但鉴于它们与计算机视觉的紧密联系，以 及它们的出处，没有把它们纳入到图像处理与分析中来。同样，这里面也有一些 也可以划归到计算机视觉中去。这都不重要，只要知道有这么个方法，能为自己 所用，或者从中得到灵感，这就够了。

8. Edge Detection
边缘检测也是图像处理中的一个基本任务。传统的边缘检测方法有基于梯度
算子，尤其是 Sobel 算子，以及经典的 Canny 边缘检测。到现在，Canny 边缘检 测及其思想仍在广泛使用。关于 Canny
算法的具体细节可以在 Sonka 的书以及 canny 自己的论文中找到，网上也可以搜到。最快最直接的方法就是看 OpenCV
的源代码，非常好懂。在边缘检测方面，Berkeley 的大牛 J Malik 和他的学生 在 2004 年的 PAMI
提出的方法效果非常好，当然也比较复杂。在复杂度要求不高 的情况下，还是值得一试的。MIT的Bill Freeman早期的代表作Steerable
Filter 在边缘检测方面效果也非常好，并且便于实现。这里给出了几篇比较好的文献，
包括一篇最新的综述。边缘检测是图像处理和计算机视觉中任何方向都无法逃避 的一个问题，这方面研究多深都不为过。
[1980] theory of edge detection
[1983 Canny Thesis] find edge
[1986 PAMI] A Computational Approach to Edge Detection
[1990 PAMI] Scale-space and edge detection using anisotropic diffusion
[1991 PAMI] The design and use of steerable filters
[1995 PR] Multiresolution edge detection techniques
[1996 TIP] Optimal edge detection in two-dimensional images
[1998 PAMI] Local Scale Control for Edge Detection and Blur Estimation
[2003 PAMI] Statistical edge detection_ learning and evaluating edge cues
[2004 IEEE] Edge Detection Revisited
[2004 PAMI] Design of steerable filters for feature detection using canny-like criteria
[2004 PAMI] Learning to Detect Natural Image Boundaries Using Local Brightness, Color, and Texture Cues
[2011 IVC] Edge and line oriented contour detection State of the art

翻译

再谈边缘检测——http://tongtianta.site/paper/56198

作者：Felice Andrea Pellegrino, Walter Vanzella, and Vincent Torre

2003年4月8日收到手稿；修订于2003年8月19日。该论文由副编辑D. Goldgof推荐。
F. A. Pellegrino现任意大利乌迪内大学数学和计算机科学系(DIMI)，乌迪内33100。
W. Vanzella和V. Torre在意大利的里雅斯特34014国际高级研究学院神经生物学系任职(电子邮件：torre@sissa.it)。
数字对象标识符10.1109 / TSMCB.2004.824147

摘要 -本手稿旨在解决边缘检测的四个问题：从细到粗的尺度同时检测所有阶跃边缘；检测宽度很少的细条；三面体连接的检测；具有图像无关参数的算法的开发。这些问题的建议解决方案将广泛的空间滤波与经典的计算机视觉方法和最新开发的算法结合在一起。通过从一大批不同比例的定向奇数滤波器求和的能量中提取局部最大值来计算阶跃边缘。通过考虑沿提供最大响应的方向在窄奇数和偶数滤波器上求和的能量的最大值来计算薄的屋顶边缘。使用定向滤波器的输出可以精确检测并恢复结点。所提出的算法对检测到的边缘的最小对比度有一个阈值：对于大量测试图像，该阈值固定为等于常规采集系统中存在的噪声标准偏差的三倍(估计为1到1.3灰度级)因此，建议的方案实际上没有参数)。在两个定量比较中，这种边缘检测方案的性能比传统的Canny边缘检测器好：从边缘图恢复原始图像和从运动任务中恢复结构。由于先前比较中的Canny检测器被证明是最好的或在最好的检测器中，因此所提出的方案比以前的方法有了显着的改进。

索引词-边缘检测，接合点检测，性能评估。

Ⅰ 引言

边缘，线条和结点通常传达图像的最相关信息[4]，[41]，[46]，因此以可靠的方式检测它们很重要。在过去的20年中，边缘检测已在计算机视觉中得到了广泛的分析[5]，[7]，[10]，[18] – [20]，[41]，但尚未完全解决。实际上，尽管付出了巨大的努力，但仍未产生出能够在所有尺度上检测和定位精确边缘的理想方案，而不论其形状和配置如何。由于缺乏明显而清晰的地面真实数据，因此难以确定最佳或理想的边缘检测方案，因此很难明确评估其性能[28]。已经提出了几种评估边缘检测方案的标准：例如，基于从运动任务中恢复结构上的三维(3-D)数据(36)，或者根据运动目标的恢复，提出了与任务有关的标准。来自边缘贴图的原始图像[28]。还提出了人类评估标准，并使用统计和心理物理工具对其进行了量化[14]，[27]。在所有这些比较中，Canny [5]的经典边缘检测方案经常(但并非总是)提供最佳性能。 该方案实质上将原始图像中的边缘识别为具有奇数方向滤波器的卷积的适当函数的局部最大值。 大约20年前提出的边缘检测方案[5]的成功表明，其本质是正确的，并且接近于最优。 众所周知，人类视觉系统能够独立于识别和推理执行理想的边缘检测。 因此，对人类视觉系统的观察可能会建议如何修改Canny的经典边缘检测方案，以便获得几乎理想的边缘检测方案。

在高等脊椎动物和哺乳动物的视觉系统中，处理的第一阶段发生在视觉区域V1中，包括视网膜图像与具有不同方向，大小和形状的滤镜的卷积[16]。 。计算机视觉也使用大量的滤镜进行图像处理。实际上，通过使用具有不同方向，大小和形状的方向滤镜对原始图像进行卷积，可以检测到边缘，拐角和其他重要的二维(2-D)特征[11]，[12]，[ 39]。当通过计算局部能量的最大值检测到二维特征时[18]，[24]，[31]，首先将图像与不同方向的奇数和偶数滤波器进行卷积。分析不同规模图像的需求，即多尺度分析[19]，[45]，现已在计算机视觉中得到广泛认可，并且是图像处理中的标准技术[13]，[22]。在所有这些比较中，Canny [5]的经典边缘检测方案经常(但并非总是)提供最佳性能。 该方案实质上将原始图像g(x，y)中的边缘标识为g(x，y)与奇数方向滤波器的卷积的适当函数的局部最大值。 大约20年前提出的边缘检测方案[5]的成功表明，其本质是正确的，并且接近于最优。 众所周知，人类视觉系统能够独立于识别和推理执行理想的边缘检测。 因此，对人类视觉系统的观察可能会建议如何修改Canny的经典边缘检测方案，以便获得几乎理想的边缘检测方案。

生物视觉和人工视觉都同意需要使用一大堆具有不同特性的滤镜来分析图像。显然，下一个问题是如何组合这些滤波器的输出。无论从生物学角度还是从计算机视觉角度来看，这都是一个重要的问题：这些滤波器的输出如何最佳集成，以检测所有比例的边缘，识别复杂性不断增加的特征并识别物体？该问题的答案可能有助于理解视觉皮层中处理的逻辑基础，并开发出高性能的计算机视觉算法。

本文的主要目的是使用在视觉区域V1中存在并实现的相当大的一组滤波器，以改进[5]中最初提出的边缘检测方案，从而获得几乎理想的边缘检测方案，能够检测：1)从细到粗的台阶边缘[24]； 2)细条，宽度不超过两个像素左右； 3)一侧对比度低的三面体连接。本文的目的还在于提供一种无需为必须检测边缘的特定图像调整任何参数的方案：实际上，所提出的边缘检测方案仅具有一个自由参数，即最小阈值 所检测到的边缘T_c的对比度被设置为等于普通采集系统中存在的噪声标准偏差的三倍。 该阈值T_c估计对应于256个灰度中的四个灰度，用于从大量测试图像中提取边缘，从而始终提供非常好的结果。

提出的边缘检测方案将几种先前建议的方法[5]，[24]，[9]，[17]与新算法结合在一起。通过使用此处描述的Mumford and Shah函数的修改版本[26]，通过此处描述的广泛过滤获得的信息也用于[42]对原始图像进行最终的正则化。此正则化步骤使用局部自适应比例和对比度，以保留较小的细节。从该正规化图像中可以获得图像分割，从而在有限数量的具有相同灰度级的区域中方便地分解图像。我们认为，这种细分几乎是用于分类和识别等高级功能的理想预处理。

本文的组织方式如下。第二节回顾了先前的工作，并概述了边缘检测的建议方法。第三节总结了计算机视觉中使用最广泛的滤镜的属性。第四节和第五节分别讨论了台阶边缘和屋顶边缘的检测，即，检测将图像的两个扩展区域(台阶边缘)分开的边缘的检测以及细条或屋顶边缘的检测。第六节论述了三面体连接的检测和恢复。第七节介绍了大量不同种类的图像的实验结果，并与以往的边缘检测方法进行了比较。第八节概述了该算法，并添加了有关噪声鲁棒性，参数灵敏度和计算时间的更多信息。

II 早期方法

边缘检测[5]，[41]的早期方法主要将其分析重点放在确定最佳微分算子上，该微分算子将强度g(x，y)的急剧变化定位在位置(x，y)。 这些方法认识到必须先进行过滤，将其识别为正则化阶段，但并未明确实现全面多尺度分析的便利性，这对于可靠检测锐利边缘和平滑边缘都是有用的[8]。 根据一些生物学的建议，Morrone和Burr [24]提出将边缘检测为获得的局部能量E(x，y)的最大值：

其中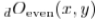和是原始图像g(x，y)在d 方向上具有正交一维滤波器对的卷积。 正交的一维滤波器对由一个均值为零，相同范数且彼此正交的偶数和一个奇对称滤波器组成。 这两个过滤器是另一个的希尔伯特变换。 随后的方法[18]建议将局部能量

即，能量在不同方向d 和尺度s 上求和。 在这些方法中，将边标识为(2)的能量的局部最大值(可能归一化)。 在一个维度上，局部能量的最大值也是最大相位一致性的点[43]，即图像中特别感兴趣的点。 当要检测的特征明显大于所用滤镜的尺寸时，能量(2)的局部最大值可正确识别边缘[18]，[24]，[31]。 当必须检测宽度小于2或3像素的条时，数字图像将不可避免地出现此问题。 解决该问题的最简单方法是对图像进行过采样，但会大大增加分析的计算负担。

通过考虑变分方法[26]，[23]，可以获得一种截然不同的边缘检测方法。 在这些方法中，通过在图像域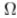上将函数k最小化，可以获得给定图像g(x，y)的边缘k 集 和合适的近似值u(x，y)，函数：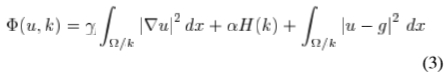

其中u(x，y)是g(x，y)的分段平滑逼近，H(k)是边的总长度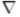，是梯度算子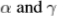，是适当的常数。 通过最小化函数(3)和通过计算(2)的局部最大值获得的边缘通常重合。 通常可以通过最小化功能(3)很好地检测给定比例的台阶边缘，但是不会检测到薄的屋顶边缘并将其涂抹。

在本文中，我们将检测和定位边缘的观点视为能量的局部最大值(2)，此外，还研究了如何将具有不同比例，方向和奇偶性的类似V1的滤波器的输出组合在一起，以“几乎理想”地检测薄屋顶的台阶边缘边缘和三面体交界处的精细和粗糙尺度。将显示出通过考虑仅由奇数滤波器的输出组成但在所有方向和比例上求和的能量(2)可以最好地检测阶跃边缘。仅考虑奇数滤波器即可获得更好性能的观察结果与Canny [5]的早期建议完全一致。相反，最好仅通过在最大响应方向上对来自狭窄的偶数和奇数滤波器的能量求和来最佳地确定薄的屋顶边缘。通过计算局部曲率可以对三面体接合点进行局部化，可以通过适当地组合偶数和奇数滤波器来获得三阶面的曲率，并通过定向滤波器的输出来精确识别它们的边。

III 滤波

在本节中，将简要回顾计算机视觉中常用的一些空间滤镜的属性：将考虑Gabor，log-Gabor和高斯滤镜。这些滤波器可以耦合以形成正交对[24]。正交的一维(1-D)滤波器对包括一个均值为零，相同范数且彼此正交的偶数和一个奇对称滤波器。这两个过滤器是另一个的希尔伯特变换。

一维Gabor滤波器是由正弦波调制的高斯函数。

其中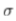是设置空间扩展的参数，w₀是调制正弦波的频率。 Gabor滤波器的傅立叶变换

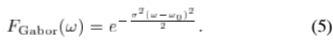
在 w=w₀ 中具有最大值。对数Gabor滤波器由其傅立叶变换定义：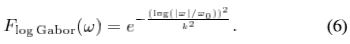

同样，在w=w₀ 中具有最大值，而k是确定频率带宽的常数。 空间域中的奇偶对数Gabor滤波器被定义为正交滤波器对的逆变换，例如，参见[32]

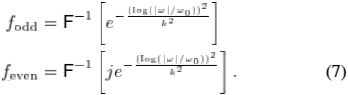
该对高斯滤波器是通过对正交滤波器对进行反变换而获得的。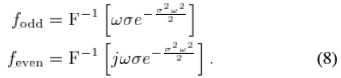

这些滤波器对于w_max = 1/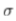 具有最大值。给定滤波器的大小被视为对应于w_max或2Π/w_max 的周期。高斯滤波器的大小仅为2Π。

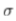偶数和奇数高斯滤波器不具有波动，但具有较宽的频谱。 当以半对数标度绘制时，对数Gabor滤波器的傅立叶变换是对称的。 Gabor滤波器的傅立叶变换最大程度地集中在w_max周围，在空间域中，它们具有明显的由正弦调制引入的纹波和振荡。

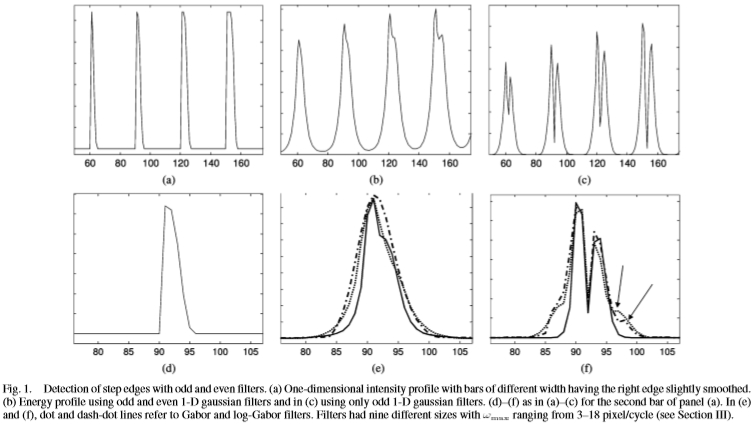
图1：用奇数和偶数滤波器检测台阶边缘。 (a)一维强度分布图，其宽度不同的条的右边缘略微平滑。 (b)使用奇数和偶数一维高斯滤波器的能量分布，而在(c)中使用仅奇数一维高斯滤波器。 (d)-(f)，如(a)-(c)所示，用于面板(a)的第二条。 在(e)和(f)中，点线和点划线是指Gabor和log-Gabor滤波器。 过滤器具有9种不同的尺寸！ 范围为3–18像素/周期(请参阅第III节)。

当进行边缘检测时，考虑到奇数和偶数滤波器输出上的能量总和，如(1)所示，Gabor，log-Gabor和高斯滤波器提供了相当相似的结果(见图1)。当仅使用奇数滤波器时(如将在下一节中所述)，由于没有波动，高斯滤波器将提供最佳结果。

一维过滤器可以通过多种方式扩展到二维。 具有傅立叶变换的二维滤波器(可分离)在极坐标中可以分解为两个函数的乘积，两个函数的一个取决于半径 p，另一个函数取决于角度。 可以使用环形楔技术来设计和实现这些滤波器(例如参见[18])。 使用该技术实现了二维Gabor和log-Gabor滤波器。

在空间域中构造二维高斯滤波器，将一维分布与高斯函数在正交方向上相乘。两个高斯函数的方差之比为1.2。以这种方式构造的二维高斯滤波器不具有波动，该波动存在于二维Gabor和log-Gabor滤波器中。

回想一下，对于在相同方向上的导数计算，方向奇数高斯滤波器的输出是一个很好的近似值，这很有用。同样，偶数均值零高斯滤波器的输出很好地近似了二阶导数。当必须计算图像强度 g(x,y) 的局部曲率时，这些说明将在以后的部分中使用。

IV 台阶边缘的检测

在本节中，我们解决了在所有范围内检测台阶边缘(即尖锐边缘和模糊边缘)的问题。如前所述，可以通过检测(1)或(2)的最大值来有效地解决组成大特征轮廓(至少五个或更多像素)的边缘检测。尺寸为2–4像素的特征边界的检测带来了一些问题。

A.奇偶过滤器的组合

让我们考虑一个理想的一维强度分布，在像素n和n + m之间具有128个灰度值，而在其他位置为1。能量(2)在n，n + m和n + m / 2中和之中具有三个局部最大值，其中前两个最大值对应于台阶边缘，而在n + m / 2处的最大值对应于屋顶边缘。当m接近三或四时，三个局部最大值合并并且不能可靠地识别。因此，必须仔细研究宽度在两个和四个像素之间的条形的检测。让我们考虑一下图1(a)所示的一维强度分布图，它由宽度逐渐增加的细条组成，具有一个尖锐的边界和一个平滑的边界。当通过对奇数和偶数高斯滤波器的输出求和来计算能量(1)时，将获得图1(b)所示的轮廓，其中宽度小于四个像素的条形图仅出现一个峰值。条形宽度大于五个像素时，将出现两个峰值。相反，如果仅使用奇数滤波器，则即使条宽仅为两个像素，也可获得对应于条的两个边界的两个峰[如图1(c)所示]。

在图1(e)和(f)中针对图1(d)所示的强度曲线比较了不同滤波器的性能，对应于图1(a)的第二条。图1(e)显示了使用偶数和奇数Gabor(虚线)，logGabor(虚线)和高斯滤波器(实线)从(1)获得的能量分布。不能很好地检测到界定条形的两个边缘，并且存在一个很大的最大值，而与组合的滤镜大小无关(有关更多详细信息，请参见后面的部分)。相反，如果仅使用奇数滤波器[见图1(f)]，则在条形边界处会明显检测到最大值。当使用Gabor和log-Gabor时，会看到其他最大值[由图1(f)中的箭头指示]。这些杂散的额外最大值是由这些滤波器的纹波产生的，当这些滤波器不用于正交对时，这些纹波变得很明显。因此，高斯滤波器优于Gabor和log-Gabor滤波器。

当考虑二维图像时，将边缘检测为能量的局部最大值(2)，该能量在八个等距方向和九个不同比例上求和(请参见下一节)。 通过修改众所周知的[46]非最大抑制算法(沿垂直于提供最高响应的滤波器的方向在每个点上执行)来检测局部最大值。 这种修改包括能量驱动的变薄，该变薄去除了可能的双边缘，即，厚度大于一个像素的边界，这可能是使用标准的非最大抑制而发生的。

图2：在二维图像中用奇数和偶数滤波器检测台阶边缘。 (a)，(d)，(g)：内部图像的细节。 (b)，(e)，(h)使用奇数和偶数滤波器将阶跃边缘检测为局部最大值。 (c)，(f)，(j)仅使用奇数滤波器检测到的阶跃边缘。 使用从三个像素/周期到18像素/周期的八个方向和九个标度。 对于奇数滤波器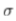，₁与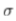₂ 的比率为1.2，而偶数滤波器为2。

图2(a)，(d)和(g)示出了内部图像的三个细节，具有宽度为2-4个像素的细条。 图2(b)，(e)和(h)显示了使用奇数和偶数高斯滤波器检测为(2)的局部最大值的边缘。 这些边缘不如仅考虑奇数滤波器时那样完整，如面板(b)，(c)，(e)，(f)，(h)和(j)清楚所示。 当使用高斯奇数滤波器时，阶梯边缘也被适当地定位在细条的特征边界处，如图2(a)和(d)所示。 不足为奇的是，仅使用奇数滤波器即可获得台阶边缘的检测，因为它们是这些特征的自然匹配滤波器[5]。 结果，仅奇数高斯滤波器将用于检测台阶边缘。

B.不同尺度的组合

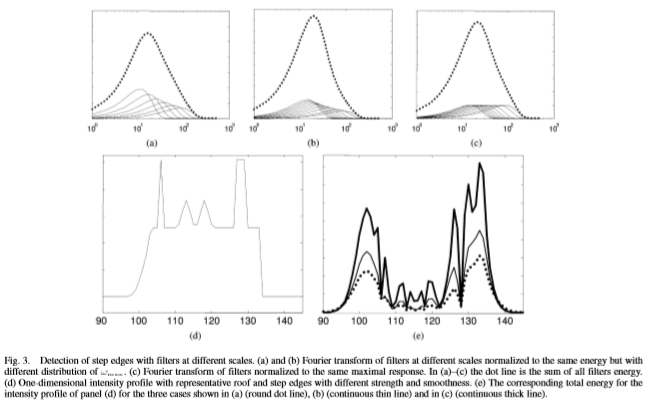
图3.用不同比例的滤波器检测台阶边缘。 (a)和(b)归一化到相同能量但w_max分布不同的不同尺度的滤波器的傅立叶变换，(c)归一化到相同最大响应的滤波器的傅立叶变换。 在(a)–(c)中，虚线是所有滤波器能量的总和。 (d)一维强度分布，具有代表性的屋顶和台阶边缘，强度和光滑度不同。 (e)在(a)(圆点线)，(b)(连续细线)和(c)(连续粗线)所示的三种情况下，面板(d)的强度分布的相应总能量。

为了在精细和粗糙尺度上检测阶跃边缘，有必要使用具有不同频率特性的小型和大型滤波器，但是如何加权它们的相对贡献并不明显。在下文中，考虑了具有9个标度的高斯滤波器(请参阅第III部分)，w_max范围从3个像素/周期到18个像素/周期。正如本文分析的那样，通过对自然图像进行的大型实验建议了这9个比例尺的选择。通过使用具有相同能量的滤波器(参见图3(a)和(b)，其中示出了中心频率的不同分布)或具有相同的最大响应，可以组合(2)中的奇数滤波器的比例。图3(c)]。这些滤波器以略有不同的方式对图像的频率内容进行采样，如相应面板(虚线)绘制的总总能量所示。图3(d)展示了一个理想的一维强度分布图，其中包含各种台阶和屋顶边缘：光滑的台阶边缘，位于两个平滑屋顶边缘之间的坚固屋顶边缘，紧随其后的尖锐台阶边缘的坚固条形。在面板e中分别以圆点，正方形和连续线显示了a，b和c中三组滤波器的相应总能量。对于具有相同最大响应的滤波器(如图3(c)所示)，总能量具有与要检测的十个特征相对应的十个局部最大值[图3(e)中的连续细线]。当对滤波器进行归一化以具有相同的能量时[如图3(a)和(b)所示，将损失几个局部最大值，如图3(e)中的点线和连续细线所示] 。

图4.在二维图像中使用不同比例的滤波器检测台阶边缘。 (a)，(d)和(g)是内部场景的细节； (b)，(e)和(h)显示了检测到的阶跃边沿，它们累加了具有相同能量并且(c)，(f)和(j)具有相同最大响应的滤波器上的能量。 使用了8个方向和9个比例，范围从3个像素/周期到18个像素/周期。 对于奇数滤波器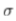，₁与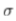₂ 的比率为1.2。

当在图像的同一区域中存在具有不同对比度和相反符号的边缘并且精细和粗糙滤镜的输出在空间上叠加时，它们的同时检测可能会很困难。大量的实验表明，某些细节[如图4(a)，(d)和(g)所示]可以通过组合具有相同最大响应的标尺来最好地检测出来(见图4(c)，(f))。 ，而不是当使用具有相同能量的滤波器时[见图4(b)，(e)和(g)]。

V  薄屋顶边缘的检测

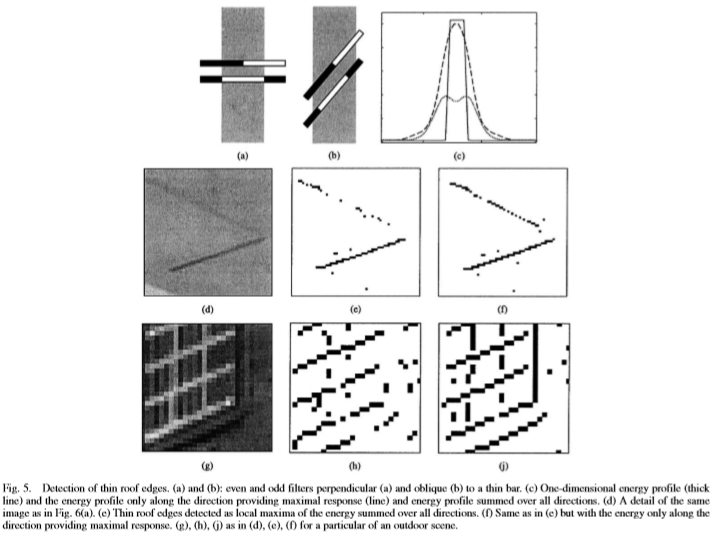
图5：薄屋顶边缘的检测。 (a)和(b)：与薄条垂直(a)和倾斜(b)的偶数和奇数滤镜。 (c)一维能量分布图(粗线)，并且仅沿提供最大响应的方向(线)分布能量图，并且能量分布图在所有方向上相加。 (d)与图6(a)相同的图像的细节。 (e)薄的屋顶边缘被检测为所有方向上能量的局部最大值。 (f)与(e)中相同，但能量仅沿提供最大响应的方向。 (d)，(e)，(f)中的(g)，(h)，(j)用于特定的室外场景。

图6.检测不同宽度的屋顶边缘。 (a)原始图像。 (b)如文中所述提取屋顶边缘图。屋顶边缘的宽度从绿色，蓝色和红色开始逐渐增加。

在本节中，将研究细棒的检测。众所周知[18]，[24]，通过同时使用偶数和奇数滤波器，可以最好地获得如图5(d)所示的细条，从而检测真实图像中的细微细节[参见图5(f) )]，当偶数滤波器的输出在条形图的中心占主导地位时，奇数滤波器的输出减小并消除了条形图边界附近的虚假最大值。如果仅使用偶数过滤器，则会在条形的中心及其边界处检测到多个最大值。在本节中，将表明，仅考虑沿最大响应方向的能量，而不考虑所有方向上的能量求和，就可以最好地检测细条，就像这样做是为了检测台阶边缘(请参阅第IV节)。

A.不汇总不同的方向

因此，结合使用偶数和奇数滤波器似乎是检测细条的最佳解决方案，但是将不同方向的偶数和奇数滤波器的电池能量求和是否方便并不明显。

如图5(a)所示垂直定向到细条的偶数和奇数滤波器的输出的总能量分布图[具有由图5(c)中的实线表示的强度分布图]具有一个大中心峰，正确位于细条的中心[请参见图5(c)中的线]。相反，当偶数和奇数滤波器不垂直于细条时(见图5(b))，总和能量的分布具有两个较小的峰[见图5(c)]。结果，在所有方向上求和对于检测对比度低的细条(如图5(d)所示)和在多个方向不同的细条(如图5(g)所示)的检测都是不利的。 。图5(d)的细条的平均对比度只有256个灰度中的五个灰度级，当仅考虑提供最大响应的方向上的能量时，可以更好地检测和定位它(请参见图5(f))。类似地，当所考虑的能量仅在最大方向上时，可以合理地很好地检测到图5(g)的细条的复杂图案。当在所有方向上对能量求和时(见图5(e)和(h))，细棒将无法很好地检测到。

B.不同规模的检测

独立检测具有不同宽度的屋顶边缘。使用宽度为四个像素的高斯滤波器检测到非常薄的屋顶边缘(宽度为一或两个像素)，并在图6(b)中以绿色显示。使用宽度为八个像素/周期的高斯滤波器检测到宽度为三个或四个像素的中等大小的屋顶边缘，并在图6(b)中以蓝色显示。用一个宽度为18像素/周期的较大滤镜检测到宽度约为5个像素的较大屋顶边缘，并在图6(b)中以红色显示。定向滤波器比用于检测台阶边缘的定向滤波器长，并且偶数和奇数滤波器的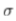₁与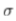₂比率均为2。根据(1)在三个尺度上计算能量。如上一节所述，提取局部最大值并应用阈值。

C.屋顶边缘的分类

一旦找到并确定了能量的最大值，仍然有必要在屋顶和台阶边缘对它们进行分类。 对边缘进行分类的常用方法[24]是比较奇数和偶数滤波器响应的绝对值：当奇数滤波器对能量的贡献大于给定值时，能量的最大值是阶跃边缘。 通过偶数过滤器 此分类程序足以对宽度大于一个像素的屋顶边缘进行分类。 宽度为一个像素的屋顶边缘的检测和分类对噪声非常敏感，因此不稳定。

将像素分类为屋顶边缘后，必须为其分配比例。 如果边仅以给定的比例出现，则将该比例分配给它。 否则，分配最小的比例。 图6(b)示出了从图6(a)所示的原始图像提取的屋顶边缘。 绝大多数屋顶边缘都是以正确的比例进行检测的。 但是，由于边缘是从能量图获得的，而该能量图没有在不同的比例和方向上求和，因此，所得的边缘图比台阶边缘的噪声更嘈杂，因此它们对噪声更敏感。

VI 三面连接的检测

图7：三面体连接处的恢复。 (a)立方体的细节。 (b)检测到的台阶边缘。 (c)归一化曲率。 (d)高曲率的感兴趣区域。 (e)感兴趣区域内的边缘图的端点。 (f)三面体交界处恢复的侧面。

图8：三面体连接恢复示例 (a)内部图像的细节。 (b)检测到的台阶边缘。 (c)台阶边缘加上恢复的连接点。 (d)脑切片的MRI图像的细节。 (e)检测到的台阶边缘。 (f)台阶边缘加上恢复的连接点。 (g)合成图像。 (h)检测到的屋顶边缘。 (j)屋顶边缘和恢复的路口。

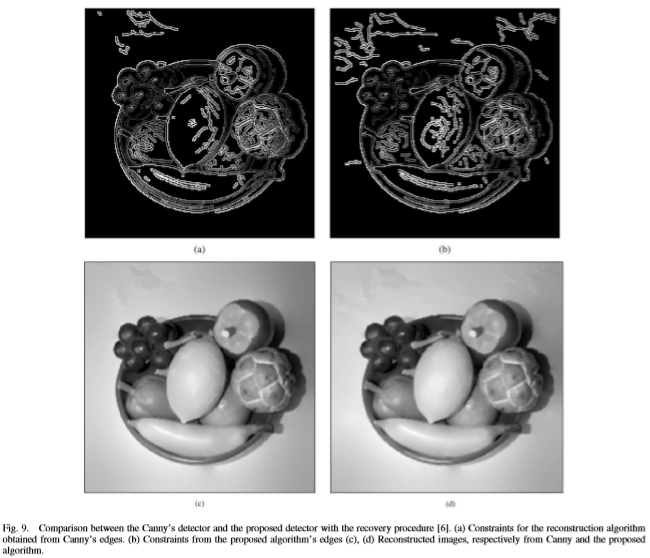
图9：Canny探测器与拟议探测器之间的比较以及恢复程序[6]。 (a)从Canny的边缘获得的重建算法的约束。 (b)分别来自Canny和所提出算法的(c)，(d)重建图像的约束。

众所周知，在存在诸如图7(a)所示的三面体连接的情况下，基于局部最大值的提取的边缘检测失败，并且边缘通常在连接处被中断[参见图7(b)]。通过以适当的方式组合类似V1的滤波器的输出，可以恢复这些重要的图像特征，而使用(2)不可避免地会丢失这些图像特征。可以通过几种方法[1]，[3]，[8]，[9]，[17]，[35]来检测可能存在三面体连接的区域，主要是通过评估局部曲率并检测其最大值。通过对[17]中提出的方法进行修改，可以将高曲率区域局部化[图9]。 7(c)]可能存在三面体连接处[图。图7(d)]。在这些区域中，可以检测到边缘线的端点[参见图7(e)]，并且可以通过使用方向局部最大值的映射来适当地恢复三面体连接的边[参见图7(f)]。 ，是单个定向滤波器能量的局部最大值的二进位图。该过程能够适当地恢复复杂且混乱图像中的缺失连接(图8中的箭头所示)。现在让我们看一下所建议程序的不同步骤。

A.局部曲率的计算

给定图像的强度分布g(x，y)，其局部曲率k为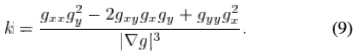

Kitchen和Rosenfeld [17]建议将可能的结点和角点确定为曲率的局部最大值k乘以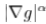。为了获得局部对比度的不变性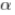，应该等于零。但是，这种选择存在许多错误的检测。 大量的实验建议使用量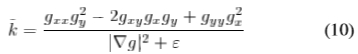

对应于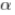=1并已引入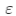，以减少梯度为零或很小时出现的失真。 等式(10)等于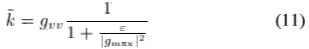

其中，g_vv是正交于梯度的方向上的二阶导数，而g_max是最大方向导数。 所有这些量都是通过此处使用的奇数和偶数滤波器的输出获得的。

B.感兴趣区域和端点的计算

通过设置一个固定的阈值来获得图像上具有高值的点，该阈值允许检测具有与垂直于强锐边缘的六个灰度级的对比度为约255个灰度级的对比度的一侧的三面体接合点。这组点被七个像素放大，因此具有足够宽的区域以包含边缘线的可能端点。在这些感兴趣的区域中，可能的终点将通过包含3 *3邻域中所有可能终点的查找表进行标识。方向与对应于“假定结点”的每个端点相关联。一旦确定了端点及其“假定结”的方向，就必须通过考虑定向滤波器的能量来验证是否假定结。总体采用的程序是

给定感兴趣区域中的一个端点，将能量最大的方向作为假定的结点方向(a指向边缘像素较少的区域)。能量是通过对定向滤波器的输出进行求和而获得的，如第四节中所使用的那样，这些求和器在九种不同的标度上求和(有关更多详细信息，请参见图2的图例)。

如果存在一连串的边缘，这些端点是定向滤波器的局部最大值，并且将这两个点连接在一起，则端点将连接到另一个边缘像素(并因此恢复连接)。

如果该连接的局部平均对比度大于八个灰度级且其总长度不超过五个像素，则最终验证该连接。

该过程能够正确地恢复复杂的真实图像中缺少的连接，例如图8(a)的内部细节和图8(d)的脑切片的MRI图像。在这两种情况下，该过程都能够恢复丢失的结点[见图8(c)和(f)]，这些结点在常规边缘检测过程中会丢失[见图8(b)和(e)]。尽管尚不清楚如何评估结点检测/恢复算法的性能，但一种可行的(简单)方法是检查该过程是否能够在人工噪声图像中提取“正确”的结点，而不会引入伪影。我们使用包含不同对比度和模糊结点的人工图像进行了这样的评估，并添加了越来越多的噪声以检查鲁棒性。我们的检测器性能非常好，可以识别和重建图像中所有正确的连接点，这些图像包含相加的正常噪声，最多可变化9个灰度。观察到正确的丢失的连接是有用的，即使端点似乎收敛的方向不正确：这种鲁棒性也主要归因于使用定向滤波器输出的验证过程。可以很容易地扩展所提出的用于恢复三面体连接的技术，以恢复薄条或屋顶边缘之间的连接[见图8(g)，(h)和(j)]。

Ⅶ 实验结果

评估边缘检测算法性能的一个主要且众所周知的问题是缺乏明确的地面真实数据(例如，参见[21])。尽管如此，仍有一些量化标准可用于评估边缘检测：例如，基于从运动任务[36]恢复结构上的3-D数据，对物体进行识别[37]以及对目标进行恢复，提出了基于任务的标准。来自边缘贴图的原始图像[28]。最后一种方法基于文献[6]中提出的重建算法，并将用于对提出的边缘检测算法进行定量评估。本节分为三个部分：在第一部分(第VII-A节)中，对先前的方法和本发明的边缘检测方案进行了定性比较；在第二部分(第VII-B节)中，[28]中已经采用的回收程序[6]用于对拟议方案进行定量评估和比较；在第三部分(VII-C节)中，讨论了针对运动[36]提出的针对任务结构的边缘检测器的性能；最后，在第四部分(第VII-D节)中，介绍了在杂乱的真实图像上的实验结果。

A.与以前方法的定性比较

提出的边缘检测器的设计和构造如下：1)在所有比例下检测台阶边缘； 2)检测薄的屋顶边缘； 3)检测三面体连接点；和4)对噪声具有鲁棒性，并且几乎没有参数。薄的屋顶边缘和三面接合处的检测是通过单独的模块获得的，如第V和VI节所述。主要通过对不同方向和比例尺上的能量求和来获得所有比例尺的阶跃边缘的检测以及对噪声的鲁棒性。然后通过查看局部最大值来检测台阶边缘。该程序具有两个主要优点：首先，它可以检测多个尺度的台阶边缘；其次，通过对多个方向和比例进行平均，消除了源自噪声的边缘，即使在较低且固定的阈值的情况下，所得的检测器也具有非常好的性能。这是所提出的边缘检测器的关键特征。

现在，将方法与以前的方法进行比较是有用的。Canny [5]于20年前提出了经典的边缘检测器，其简单，优雅的表现非常出色。确实，在最近对边缘检测器性能的比较中[14]-[36]，Canny检测器是最好的或最好的之一。Canny的边缘检测器试图同时最大化定位和信噪比。因此，检测台阶边缘的最佳方法是使用形状类似于高斯函数导数的奇数方向滤波器对图像进行滤波。这个结论与第四节中的讨论非常相似。Canny的边缘检测器有两个缺点：首先，它无法同时检测两个非常不同的比例的台阶边缘；其次，三面体连接处无法正确检测，并且经常在不同的部分断开。

在[36]中已经讨论并比较了不同的边缘检测器，这里只给出了一个简短的定性比较。 Deriche [7]以及Shen和Castan [38]提出的边缘检测器与Canny的检测器具有相同的结构，但是使用了不同的方向滤波器。 对于Deriche，定向滤波器为，Shen和Castan的方向滤波器为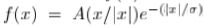。Shen和Castan使用的滤波器在零处不连续，因此对噪声非常敏感。 [34] – [38]中提出的检测器使用单一标度和基于梯度的方法。 SUSAN检测器[40]具有完全不同的方法，并且基于非线性，单尺度滤波。

多个作者[2]，[10]，[19]使用了多个量表。我们的方法与这些方法的不同之处在于处理和合并不同规模的方式。

Kovesi [18]提出了通过观察相全而不是能量的最大值来检测边缘。 相位一致是正确归一化的能量。 能量在具有不同比例和方向的滤波器输出上求和，条件是该能量高于与最小滤波器的输出能量相关的阈值。 然而，与我们相反，科维西对奇数和偶数滤波器进行求和，因此他的方法遇到了图2和3所述的问题。 参见图2和3。[33]的方法与[18]的方法相似，但范围相同。

最近，已经提出了一种多特征技术[21]，其中使用人类标记图像作为地面实况来训练分类器。带有人类标签的图像代表了少数区域(20–30)中图像的分割，该算法更适合作为边界检测器。而且，它生成概率图而不是二进制边缘图。因此，将提出的检测器与Martin和合著者之一[21]进行比较是不合适的。

B.与以前的方法进行定量比较：从边缘恢复图像[34]

Carlsson [6]提出了以下步骤，从边缘图k 中恢复原始图像g(x，y)。首先，将该边缘图k扩大1个像素，从而获得集合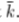。其次，将原始灰度值g(x，y)与(x，y)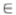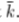用作内插值，以最小化(离散形式的)函数

函数 r(x，y)在约束下最小化(12)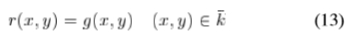

是恢复的图像。可以通过计算两个误差来评估恢复的质量，这两个误差定义为：绝对绝对误差(MAE)和均方根误差(RMSE)：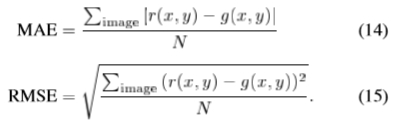

当内插边缘k的基数即总数大时，以及当内插点k出现在原始图像g(x，y)的最相关特征处时，这两个误差将很小。在[28]中使用了最后一个标准来进行边缘检测器之间的定量比较。我们将本文提出的用于边缘检测的程序与Canny在包括[28]中使用的，由作者友善地提供给我们的图像上进行比较。 Carlsson提出的技术仅涉及台阶边缘，因此仅涉及使用din(12)–(13)的台阶边缘和台阶结。我们的结果与[28]中报道的结果之间的差异很可能源自基于高级梯度下降(粗体驱动器；请参见[44])的函数(12)最小化的改进。图9显示了从Canny的边缘图(a)，(c)和所提议的技术(b)，(d)恢复原始图像的比较.Canny检测器的参数通过在参数空间中的穷举搜索来优化：高斯滤波的sigma通过取29个等距值从0.2采样到3，并通过取16个等距值从2到32个灰度级采样滞后步骤中的高阈值。设置第三参数，即低阈值，使得对于两个检测器，插值边缘的基数相同。因此，对于每张图像16 * 29 = 464，Canny的检测器考虑了不同的参数设置(并非所有参数都导致第三个参数的可行选择)。选择了最低的RMSE和MAE(可能来自不同的设置)。在所提出的算法中，插值边的空间位置相对于Canny中的一个稍微不同，Canny产生的地图在尖锐边缘附近更密集，在平滑边缘附近几乎是空的。结果，从我们的边缘贴图中恢复的图像的错误率比从Canny边缘获得的图像的误差要低。根据[6]的恢复过程，Canny的边缘检测器和我们的边缘检测器之间的性能比较在表I中显示了各种图像。在9张图片中，有6张使用了边缘检测器，相对于Canny而言，其恢复误差较低。对于九张分析的图像，我们的探测器的平均误差为11.62(MAE)和19.53(RMSE)，而Canny的探测器的平均误差为12.02(MAE)和20.17(RMSE)。表Ⅰ所示的数据值得一提。从非常稀疏的边缘贴图恢复的图像(例如“坚果”图像)具有较大的MAE和RMSE值。恢复性能差的主要原因是约束密度非常低，即约占总像素的5％，而不是因为提取的边缘不正确。即使存在高密度约束，即几乎50％的约束条件，也可以恢复具有许多细微细节的图像，例如图像“ Sherbrooke”。这个大错误是由于图像的复杂性。在主要具有锐利边缘的图像中，Canny的检测器性能相当好：事实上，在经过充分研究的Lena图像中，Canny的边缘检测器的性能略好于我们的检测器。我们的边缘检测器在具有许多不同比例尺边缘的图像方面表现出色。

表Ⅰ  提议的算法与Canny算法从边缘图像中恢复的比较[6]

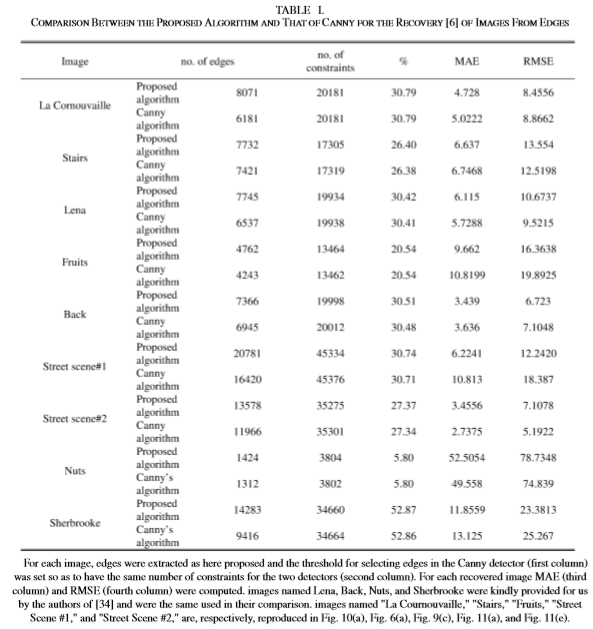
对于每个图像，按照此处的建议提取边缘，并设置Canny检测器(第一列)中选择边缘的阈值，以使两个检测器(第二列)具有相同数量的约束。 对于每个恢复的图像，计算MAE(第三列)和RMSE(第四列)。 [34]的作者为我们提供了名为Lena，Back，Nuts和Sherbrooke的图像，它们在比较中也使用相同的图像。 在图10(a)，图6(a)中分别复制了名为“ La Cournouvaille”，“楼梯”，“水果”，“街景＃1”和“街景＃2”的图像， 图9(c)，图11(a)和图11(e)。

C.与先前方法的定量比较：运动的结构[36]

Shin和合著者[36]提出了从运动中恢复结构(SFM)的方法，作为在边缘检测器之间进行定量比较的一种方法。 这种比较是在从检测到的边缘和直接测量的地面真实“结构”和“运动”数据中恢复的参数之间进行的，从而导致“结构误差”和“运动误差”。“结构误差”是度的绝对差 在计算和测量的角度之间的“运动误差”是估计给定点绕旋转轴旋转时的百分比误差。

在[36]中比较了18个不同的木块和乐高房屋图像序列上的八个不同的边缘检测器。通过搜索最佳参数集(表征每个检测器)来优化不同检测器的性能。对于每个图像序列，考虑通过最小化“结构误差”和“运动误差”的参数获得的性能。在此比较中，由于SFM算法基于长直线，因此仅使用长边和直边链。结果，不考虑短边缘链或长圆形边缘链。另外，所使用的图像序列具有主要是锐利的边缘，在精细规模上可以更好地检测到，因此比较了检测器的主要检测长而锐利的边缘的能力。基于一组手动选择的参考线，可以自动获取长边链之间的对应关系，从而恢复结构和运动。对于SFM的任务而言，必不可少的匹配算法偏爱粗线，从而使通信更加容易。比较结果表明，在此SFM任务中，Canny的边缘检测器提供的错误最少，其次是Heitger的检测器。

使用Shin教授提供的软件和图像，将拟议的边缘检测器和Canny检测器对18个序列进行了比较。最初，所提议的边缘检测器的性能并未得到优化，即，用于SFM任务的边缘是如第IV和VII-A节所述的那些边缘。参数优化后，Canny探测器的性能是在[36]中获得的。该比较示于表II。

表II 运动任务的结构与拟议算法的比较[42]。

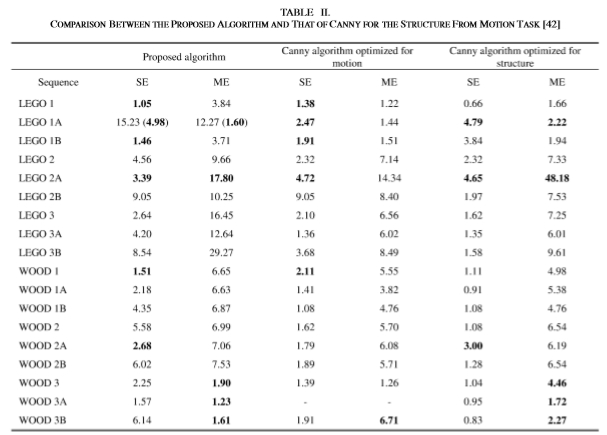
在18个序列中的8个序列中，我们的检测器在没有任何参数优化的情况下，在结构或运动恢复方面提供了较低的误差。 当使用传统的非最大抑制算法并获得稍粗的边缘链时，该检测器的性能得到了显着改善。 为获得较细的边缘链而引入的改进的非最大抑制算法减少了线之间的对应关系，从而导致性能下降。 这样，大大减少了所提出的检测器的“结构误差”和“运动误差”。 对于我们的探测器性能最差的图像序列LEGO1A，结构和运动任务的两个误差分别从15.23降低到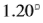和从12.27％降低到1.80％，并且我们的探测器的性能明显优于Canny的探测器。 因此，我们的检测器在没有任何优化的情况下，其性能与Canny的检测器相当。

D.实验结果的选择

现在让我们看看所提出的边缘检测器如何在各种自然的复杂图像中执行。 在具有相同参数，尤其是具有四个灰度级的相同阈值T_c的所有图像中检测到台阶边缘(请参见第IV节)。

图10. Cornouaille船的边缘检测。 (a)原始图片，分辨率为512 * 512像素。 (b)在256 * 256像素的采样图像中，检测到的黑色阶跃边缘为红色，恢复的三面体交界为红色。 (c)来自以256 * 256像素采样的图像的细节，具有许多不同宽度的薄屋顶以及由淡云产生的平滑台阶边缘。 (d)黑色为台阶边缘，蓝色(较小宽度)，绿色(中等宽度)和红色(较大屋顶边缘)的屋顶边缘。 观察箭头未指示的薄屋顶边缘。 (e)与(c)中相同的细节，但为512 * 512像素。 (f)从(e)所示的细节中检测到台阶边缘。 观察到薄的屋顶边缘几乎被完全检测到。

图10(a)是一个有趣的图像(“ La Cornouvaille”)，其中，绳子和电线杆产生了许多宽度不同的薄屋顶。在图10(b)中，检测到的台阶边缘显示为黑色，恢复的接合面显示为红色。边缘非常干净，几乎总是在观察到边缘的地方出现。在大的感知均匀区域，例如天空和船底，几乎没有边缘。同样，可以正确检测出大部分感知边缘。屋顶边缘被很好地检测到[图。图10(d)]的细节。 10(c)]代表悬挂的绳索和杆子。观察到未检测到细绳[参见图10(d)中的白色箭头]。由于能量是在许多尺度上求和的，其强力边缘源自近乎黑色的垂直极点，因而使对细绳的检测变得模糊。

实际上，当低对比度的屋顶边缘接近高对比度的边缘时(如图10(c)所示)，第一个通常会丢失。当必须使用扩展到三个或五个像素的非常小的滤镜时，也会出现此问题。在这种情况下，高斯滤波器的采样不充分，数字滤波不能提供良好的结果也就不足为奇了。当分析相同的图像但分辨率更高时(或简单地对原始图像进行过采样)，此问题将大大减少甚至消除[参见图10(e)]。边缘可以更好地检测和定位[Fig。 10(f)]在512*512像素的图像中。

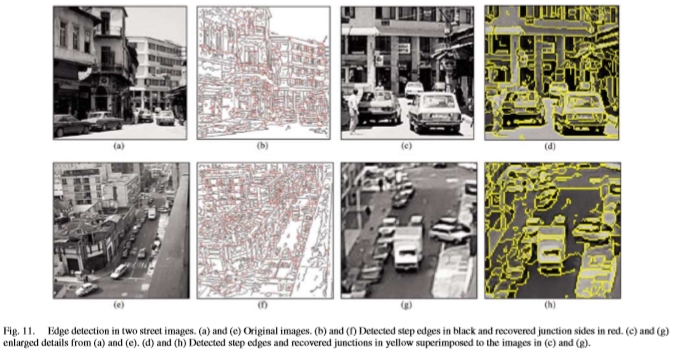
图11.两个街道图像中的边缘检测。 (a)和(e)原始图像。 (b)和(f)检测到的台阶边缘为黑色，恢复的接合面为红色。 (c)和(g)放大了(a)和(e)的细节。 (d)和(h)与(c)和(g)中的图像重叠的黄色检测到的台阶边缘和恢复的结。

图11(a)和(e)再现了两个凌乱的街道场景。图11(b)和(f)分别以黑色和红色显示了检测到的台阶边缘和恢复的接合边。

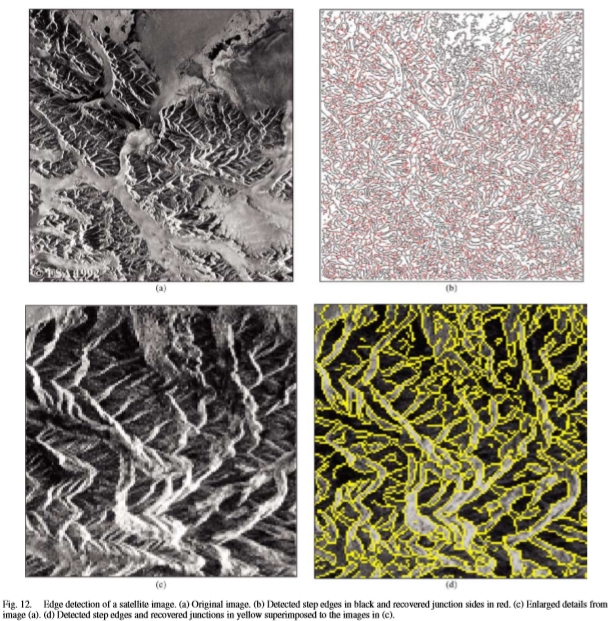
图12.卫星图像的边缘检测。 (a)原始图像。 (b)检测到的台阶边缘为黑色，恢复的接合面为红色。 (c)放大图(a)中的细节。 (d)与(c)中的图像重叠的黄色检测到的台阶边缘和恢复的结点。

图13：复杂自然场景中的边缘检测。 (a)和(b)原始图像。 (b)和(d)与(a)和(c)中的图像重叠的黄色检测到的台阶边缘和恢复的结。

这两个图像的细节在图11(c)和(g)中示出。在图11(e)和(h)中，检测到的边缘(台阶边缘和恢复的侧接点)以黄色显示，与原始灰度重叠。同样在这种情况下，所提出的方案检测到几乎所有可见特征并且对噪声具有鲁棒性。图12(a)展示了一个非常复杂的，具有精细纹理的卫星图像，该图像源自地形地质。图12(b)分别以黑色和红色显示了检测到的台阶边缘和恢复的接合边。正确检测到所有相关的局部亮度变化，如图12(d)中黄色边缘所示。对图像强度局部变化的定位，准确性和敏感性相当出色。最后，图13(a)和(c)展示了两个自然的，高度纹理化的图像，其中包含许多细节以及锐利而平滑的边缘。如图13(b)和(d)所示，几乎可以完美检测所有边缘。请注意，在两个图像的平坦背景中都完全没有检测到边缘。

Ⅷ 总结

本文讨论了边缘检测的四个经典问题：1)从细到粗的尺度检测所有阶梯边缘； 2)检测细条，即屋顶边缘； 3)三面体连接处及其侧面的检测； 4)开发了几乎没有参数的边缘检测器。提议的边缘检测方案使用了多种具有不同方向，形状和大小的滤波器，如先前的几篇论文[4]，[11]，[18]，[19]，[25]，[29]所建议的那样。 [30]，[39]。这里提出的三面体连接的检测和恢复是基于已经提出的用于计算局部曲率的技术[17]，并利用了适当的验证程序。

如第七节所述，拟议的边缘检测器是从以前的方法中汲取灵感的，并且是对原始Canny检测器的改进。 它确实能够检测到不同比例的三面体交界处和边缘，这是原始Canny探测器无法发现的特征。 根据SFM任务(请参阅VII-B节)和从边缘图恢复原始图像(请参阅VII-C节)进行的定量比较表明，建议的探测器性能要优于Canny探测器。 在不同种类的图像上进行的广泛实验(请参阅第VII节)表明，所提出的方案可检测到原始图像中感知到的所有边缘(偶尔有例外)。 另一方面，所有检测到的边缘在视觉上都存在于原始图像中。 因此，我们认为所提出的方案代表了对现有边缘检测器的重大改进。 现在让我们总结主要问题和结论。

A.台阶边缘的检测

通过查看求和能量(2)的局部最大值来检测台阶边缘，其中求和仅在奇数高斯滤波器上，沿着八个不同方向以及从3到18像素/周期的九个比例范围内扩展。对不同尺度的滤波器进行归一化，以使其具有相等的最大响应[见图3(c)]和不相等的能量[参见第四节]。假设成像设备的噪声在1.3灰度级附近具有标准偏差A [10]；结果，对比度大于6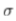= 8灰度级的所有边缘都不能源自随机波动，而必须是有意义的感知特征。对比度低于3 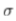= 4灰度级的边缘被拒绝，并且根据第四部分讨论的磁滞标准选择对比度在4到8灰度级之间的边缘。该固定阈值已用于提取纸张中显示的所有图像中的边缘，它是所提出的边缘检测器的唯一相关参数。使用如此低的阈值的可能性是通过对许多方向和范围内的定向滤波器的输出求和而获得的噪声消除的结果。这种方法的一个缺点是在不同比例的边缘之间可能存在干扰：实际上，高对比度的平滑边缘会使附近低对比度的锐利边缘的检测更加困难(见图10)。

仅使用奇数滤波器而不是同时使用奇数和偶数滤波器来检测台阶边缘的原因[24]，[18]与Canny在1986年使用具有高斯一阶导数形状的定向滤波器来检测边缘的方法基本相同。功能(请参阅第VII-A节)。

B.屋顶边缘的检测

细条或屋顶边缘的检测比台阶边缘的检测对噪声更敏感。实际上，可以使用非常窄的滤光片来检测宽度大约为一个像素的屋顶边缘，该滤光片的规模很小，大约三个或四个像素/周期。这些狭窄的滤波器不能像大型滤波器那样被很好地采样并且不能去除噪声。另一方面，用所有方向的滤波器都无法获得较大条形的检测结果(见图6)，因此噪声去除较少。与以前的方法[18]一致，[33]最好同时使用奇数和偶数滤波器来检测屋顶边缘(请参阅第V节)。

C.三面体连接点的检测

提议的三面体连接的检测和丢失侧的恢复很大程度上受到先前方法的启发[17]。主要区别在于基于定向滤波器输出分析的验证步骤。此过程似乎能够正确还原绝大多数丢失的面。

D.噪声稳健性，参数灵敏度和计算时间

所提出的边缘检测器并不简单，并且具有许多参数，例如不同方向的数量(八个方向)，最小和最大滤镜的大小(三个和19个像素/周期)，用于构造的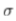₁和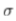₂之间的比率 定向滤波器(1.2)。通过将最大滤镜增加到40个像素/周期，将定向滤镜的方向数增加到16个，或将比率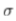₁和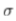₂更改为两个，或将交界检测的参数值修改50％而获得的边缘图几乎无法区分。实际上，至少95％的边缘是所有这些边缘图所共有的。当必须检测到非常大的台阶边缘时(或处理非常高分辨率的图像时)，可能有必要扩展最大滤镜的尺寸。

如已经讨论的，在检测到的边缘的对比度上有一个阈值，对应于四个灰度级。更改此值将大大改变检测到的边缘数量。但是，对大量图像进行的相当广泛的实验表明，可以始终使用该阈值并将其设为固定值。1 因此，所提出的边缘检测器几乎可以认为没有参数。

1对于噪声很大的图像，例如在超声心动图期间获得的图像，可以增加此阈值。更一般而言，当处理特定类别的图像时，可以对阈值进行微调。在这些情况下，一种可能的解决方案是估计传感器噪声并相应地设置阈值。已经提出了许多方法来估计噪声：例如，在[10]中，传感器噪声被建模为平稳的加法零均值白噪声过程：然后，通过高通滤波来计算分布的标准偏差。图像的“几乎平坦”的区域。

拟议的边缘检测器使用Matlaband在OS Windows 2000下具有Athlon 1.1 GHz处理器的PC，需要大约120s来提取256 * 256像素图像中的边缘。通过使用低级语言并优化代码(并考虑到大多数计算 (可以并行执行)，可以大大减少时间。

E.拟议方案失败

尽管声称所提出的边缘检测方案几乎是理想的，但它在两种情况下都失败了。当低对比度边缘非常接近高对比度边缘时(如图10(c)所示)，低对比度边缘经常会丢失。同样，不能可靠地检测到宽度仅为一个像素的屋顶边缘。当必须使用扩展到三或五个像素的非常小的滤镜时，就会产生这些问题。在这种情况下，高斯滤波器的采样不充分，数字滤波不能提供良好的结果也就不足为奇了。当使用相同的图像但分辨率更高时，或者更简单地对原始图像进行过采样时，几乎可以完全消除这两个问题。

致谢

作者要感谢C. Morrone进行的许多有益的讨论和有益的建议，并感谢G. Musso和A. Verri对手稿的初稿进行了阅读和评论。他们还感谢T. Nguyen，D。Ziou，D。Goldgof和M. Shin提供了用于比较边缘检测器的代码和图像。最后，他们感谢L. Hall亲切解决了一个复杂的文件传输问题。

参考文献

[1] P.R.Beaudet,“Rotationalinvariantimageoperators,”inProc.Int.Conf. Pattern Recognition, 1978, pp. 579–583.
[2] F. Bergholm, “Edge focusing,” IEEE Trans. Pattern Anal. Machine Intell., vol. PAMI-9, pp. 726–741, 1987.
[3] K. Brunnstrom, T. Lindeberg, and J. O. Eklundh, “Active detection and classificationofjunctions,”inProc.2ndEur.Conf.ComputerVision,St. Margherita Ligure, Italy, 1992, pp. 701–709.
[4] D. Burr and M. C. Morrone, “A nonlinear model of feature detection,” in Nonlinear Vision, Determination of Receptive Field, Function and Networks. Boca Raton, FL: CRC, 1992.
[5] J.F.Canny, “Acomputationalapproachtoedgedetection,”IEEETrans. Pattern Anal. Machine Intell., vol. 8, pp. 679–698, Sept. 1986.
[6] S. Carlsson, “Sketch based coding of gray level images,” Signal Process., no. 15, pp. 57–83, 1988.
[7] R.Deriche,“UsingCanny’scriteriatoderivearecursivelyimplemented optimal edge detector,” Int. J. Comput. Vis., vol. 1, no. 2, pp. 167–187, 1987.
[8] R. Dericheand G. Giraudon, “A computational approach for corner and vertexdetection,”Int.J.Comput.Vis.,vol.10,no.2,pp.102–124,1993.
[9] L. Dreschler and H. H. Nagel, “On the selection of critical points and local curvature extrema of region boundaries for interframe matching,” in Proc. Int. Conf. Pattern Recognition, 1982, pp. 542–544.
[10] J.H.ElderandS.W.Zucker,“Localscalecontrolforedgedetectionand blurestimation,”IEEETrans.Pattern Anal.MachineIntell.,vol.20, pp. 699–716, July 1998.
[11] W. T. Freeman and E. H. Adelson, “The design and use of steerable filters,” IEEETrans. PatternAnal.MachineIntell.,vol.13, pp.891–906, Sept. 1991.
[12] W. T. Freeman, “Steereable filters and local analysis of image structures,” Ph.D. dissertation, Dept. Media Arts Sci., Mass. Inst. Technol., Cambridge, 1992.
[13] A. Grossman, “Wavelet transforms and edge detection,” in Stochastic Processes in Physics and Engineering, S. Albeverio, P. Blanchard, M. Hezewinkel,and L. Streit, Eds. Amsterdam, TheNetherlands: Reidel, 1988, pp. 149–157.
[14] M. Heath, S. Sarkar, T. Sanocki, and K. W. Bowyer, “A robust visual method for assessing the relative performance of edge-detection algorithms,” IEEE Trans. Pattern Anal. Machine Intell., vol. 19, pp. 629–639, Dec. 1997.
[15] M. Heath, S. Sarkar, T. Sanocki, and K. W. Bowyer, “Comparison of edge detectors: A methodology and initial study,” Comput. Vis. Image Understand., vol. 69, no. 1, pp. 38–54, 1998.
[16] D. H. Hubel and T. N. Wiesel, “Receptive fields and functional architecture in two nonstriate visual areas (18 and 19) of the cat,” J. Neurophysiol., no. 28, pp. 229–289, 1965.
[17] L. Kitchen and A. Rosenfeld, “Gray-level corner detection,” Pattern Recognit. Lett., vol. 1, no. 2, pp. 95–102, 1982.
[18] P. Kovesi, “Image features from phase congruency,” in Videre. Cambridge, MA: MIT Press, 1999, vol. 1, pp. 1–26.
[19] T. Lindeberg, “Edge detection and ridge detection with automatic scale selection,” Int. J. Comput. Vis., vol. 30, no. 2, 1998.
[20] D.MarrandE.Hildreth,“Theoryofedgedetection,”inProc.RoyalSoc. London B, 1980, pp. 187–217.
[21] D. R. Martin, C. C. Fowlkes, and J. Malik, “Learning to detect natural image boundaries using brightness and texture,” in Proc. NIPS, Vancouver, BC, Canada, 2002.
[22] Y. Meyer, Wavelets—Algorithms and Applications. Philadelphia, PA: SIAM, 1993.
[23] J. N. Morel and S. Solimini, Variational Methods in Image Segmentation. Boston, MA: Birkhauser, 1995.
[24] M. C. Morrone and D. Burr, “Feature detection in human vision: A phase-dependent energy model,” in Proc. Royal Soc. London B, 1988, pp. 221–245.
[25] M.C.MorroneandR.A.Owens,“Featuredetectionfromlocalenergy,” Pattern Recognit., no. 6, pp. 303–313, 1987.
[26] D. Mumford and J. Shah, “Optimal approximation of piecewise smooth functionandassociatedvariationalproblems,”Commun.Pure Applicat. Math., no. 42, pp. 577–685, 1989.
[27] D. Nair, A. Mitiche, and J. K. Aggarwal, “On comparing the performance of object recognition systems,” in Proc. Int. Conf. Image Processing, 1995, pp. 631–634.
[28] T. B. Nguyen and D. Ziou, “Contextual and noncontextual performance evaluation of edge detectors,” Pattern Recognit. Lett., no. 21, pp. 805–816, 2000.
[29] P. Perona and J. Malik, “Scale-space and edge detection using anisotropic diffusion,” IEEE Trans. Pattern Anal. Machine Intell., vol. 12, pp. 629–639, 1990.
[30] P. Perona and J. Malik, “Detecting and localizing edges composed of steps, peaks androofs,” in Proc. 3rd Int.Conf. Computer Vision, Osaka, Japan, 1990, pp. 55–57.
[31] B. Robbins and R. Owens, “2D feature detection via local energy,” Image Vis. Comput., no. 15, pp. 353–368, 1997.
[32] R. Rodriguez-Sanchez, J. A. Garcia, J. Fdez-Valdivia, and X. R. Fdez-Vidal, “The RGFF representational model: A system for the automatically learned partioning of visual patterns in digital images,” IEEE Trans. Pattern Anal. Machine Intell., vol. 21, pp. 1044–1073, Oct. 1999.
[33] L. Rosenthaler, F. Heitger, O. Kubler, and R. von der Heydt, “Detection of general edges and keypoints,” in Proc. ECCV, 1992, pp. 78–86.
[34] C. A. Rothwell, J. L. Mundy, W. Hoffman, and V. D. Nguyen, “Driving vision by topology,” in Proc. SCV, 1995, pp. 395–400.
[35] M.A.RuzonandC.Tomasi,“Edge,junction,andcornerdetectionusing color distributions,” IEEE Trans. Pattern Anal. Machine Intell., vol. 23, pp. 1281–1295, Nov. 2002.
[36] M. C. Shin, D. B. Goldgof, K. W. Bowyer, and S. Nikiforou, “Comparison of edge detection algorithms using a structure from motion task,” IEEE Trans. Syst., Man, Cybern. B, vol. 31, pp. 589–601, Aug. 2001.
[37] M.C.Shin, D.B.Goldgof,andK.W.Bowyer, “Comparison of edge detector performance through use in an object recognition task,” Comput. Vis. Image Understand., vol. 84, no. 1, pp. 160–178, 2001.
[38] J. Shen and S. Castan, “An optimal linear operator for edge detection,” Comput. Vis. Graph. Image Process., vol. 54, no. 2, pp. 122–133, 1992.
[39] E. P. Simoncelli and H. Farid, “Steerable wedge filters for local orientation analysis,” IEEE Trans. Image Processing, vol. 5, pp. 1377–1382, Sept. 1996.
[40] S. M. Smith and J. M. Brady, “SUSAN—A new approach to low level image processing,” Int. J. Comput. Vis., vol. 1, no. 23, pp. 45–78, 1997.
[41] V. Torre and T.A. Poggio, “On edgedetection,” IEEE Trans. on Pattern Anal. Machine Intell., vol. 8, pp. 148–163, Mar. 1986.
[42] W. Vanzella, F. A. Pellegrino, and V. Torre, Regularization and segmentation of natural images, in IEEE Trans. Pattern Anal. Machine Intell., June 2004, to be published.
[43] S.VenkateshandR.A.Owens,“Ontheclassificationofimagefeatures,” Pattern Recognit. Lett., no. 11, pp. 339–349, 1990.
[44] T. P. Vogl, J. W. Mangis, A. K. Rigler, W. T. Zink, and D. L. Alkon, “Accelerating the convergence of the back-propagation method,” Biol. Cybern., no. 59, pp. 257–263, 1988.
[45] A. Witkin, “Scale-space filtering,” in Proc. Int. Joint Conf. Artificial Intelligence, 1983, pp. 1019–1022.
[46] D. Ziou and S. Tabbone, “Edge detection techniques-An overview,” Dept. Math Comput. Sci., Univ. Sherbrooke, Sherbrooke, QC, Canada, Tech. Rep. 195, 1997

2