[bzoj 3701] Olympic Games (莫比乌斯反演)

题目描述

• 给出n,m,l,r,modn,m,l,r,modn,m,l,r,mod
• 表示一个(n+1)∗(m+1)(n+1)*(m+1)(n+1)∗(m+1)的格点图,求能够互相看见的点对个数对modmodmod取模的值.
• 能互相看见定义为此两点连线上没有其他的格点且欧氏距离在[l,r]范围内
• n,m&lt;=100000l,r&lt;=150000mod&lt;=109n,m&lt;=100000\newline l,r&lt;=150000\newline mod&lt;=10^9n,m<=100000l,r<=150000mod<=109

题目分析

• 首先我们将上下左右相邻的点对特判:
  
  当l&lt;=1&lt;=rl&lt;=1&lt;=rl<=1<=r时有(2nm+n+m)(2nm+n+m)(2nm+n+m)个上下左右相邻点对对答案造成贡献

• 此时我们只需要找出某个长宽互质矩形的对角线(两条)能够对答案造成多少贡献即可,如图,在长宽为(5,3)(5,3)(5,3)的矩形中,长宽为(1,2)(1,2)(1,2)的子矩形的副对角线对答案造成了((5+1)−1)((3+1)−2)((5+1)-1)((3+1)-2)((5+1)−1)((3+1)−2)的贡献:
  
  
  
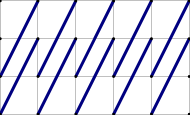
  所以在求某个矩形造成的总贡献时就用一条对角线的贡献乘以222即可
  
  Ans=2∑x=1n∑y=1m[(x,y)==1](n+1−x)(m+1−y)Ans = 2\sum_{x=1}^n\sum_{y=1}^m[(x,y)==1](n+1-x)(m+1-y)Ans=2x=1∑n​y=1∑m​[(x,y)==1](n+1−x)(m+1−y)
  
  =2∑x=1n((n+1−x)∑d∣xμ(d)∑d∣ym(m+1−y))=2\sum_{x=1}^n((n+1-x)\sum_{d|x}\mu(d)\sum_{d|y}^m(m+1-y))=2x=1∑n​((n+1−x)d∣x∑​μ(d)d∣y∑m​(m+1−y))
  
  =2∑x=1n((n+1−x)∑d∣xμ(d)∑y=1⌊md⌋(m+1−yd))=2\sum_{x=1}^n((n+1-x)\sum_{d|x}\mu(d)\sum_{y=1}^{⌊\frac md⌋}(m+1-yd))=2x=1∑n​((n+1−x)d∣x∑​μ(d)y=1∑⌊dm​⌋​(m+1−yd))
  
  由于∑y=1⌊nd⌋(m+1−yd)\sum_{y=1}^{⌊\frac nd⌋}(m+1-yd)∑y=1⌊dn​⌋​(m+1−yd)可以Θ(1)\Theta(1)Θ(1)求
  
  所以Θ(n)\Theta(n)Θ(n)枚举xxx,Θ(n)\Theta(\sqrt n)Θ(n​)枚举d即可
  
  总时间复杂度Θ(nn)\Theta(n\sqrt n)Θ(nn​)

Tips

• 此处还有[l,r]的限制,首先考虑[1,k]怎么做
  
  只用满足x2+y2&lt;=k2x^2+y^2&lt;=k^2x2+y2<=k2即可
  
  则
  
  Ans(k2)=2∑x=1n((n+1−x)∑d∣xμ(d)∑y=1⌊min(m,k2−x2)d⌋(m+1−yd))Ans(k^2)=2\sum_{x=1}^n((n+1-x)\sum_{d|x}\mu(d)\sum_{y=1}^{⌊\frac {min(m,\sqrt{k^2-x^2})}d⌋}(m+1-yd))Ans(k2)=2x=1∑n​((n+1−x)d∣x∑​μ(d)y=1∑⌊dmin(m,k2−x2​)​⌋​(m+1−yd))
• 对于[l,r][l,r][l,r],答案就是Ans(r2)−Ans(l2−1)Ans(r^2)-Ans(l^2-1)Ans(r2)−Ans(l2−1)
  
  此处不能用rrr与l−1l-1l−1作为参数代进去,因为两点距离的值域为RRR,不一定为整数,会多减一部分答案

AC code

#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 100005;
int n, m, mod, l, r, ans;

int Prime[MAXN], Cnt, mu[MAXN];
bool IsnotPrime[MAXN];
void init()
{
	mu[1] = 1;
	for(int i = 2; i < MAXN; ++i)
	{
		if(!IsnotPrime[i])
			Prime[++Cnt] = i, mu[i] = -1;
		for(int j = 1; j <= Cnt && Prime[j] * i < MAXN; ++j)
		{
			IsnotPrime[Prime[j] * i] = 1;
			if(i % Prime[j] == 0)
			{
				mu[Prime[j] * i] = 0;
				break;
			}
			mu[Prime[j] * i] = -mu[i];
		}
	}
}

inline int F(int k, int d)
{
	return (1ll * k * (m+1) % mod - 1ll * d * ((1ll*k*(k+1)/2) % mod) % mod) % mod;
}

inline int solve(long long k) // y*y <= k*k - x*x
{
	int ret = 0;
	for(int x = 1; x <= n && 1ll*x*x < k; ++x)
	{
		int s = 0, up = min(m, int(sqrt(1.0*k-1.0*x*x)));
		for(int d = 1, d2; d*d <= x; ++d) if(x % d == 0)
		{
			s = (s + 1ll * mu[d] * F(up/d, d) % mod) % mod;
			if(d != (d2=x/d))
				s = (s + 1ll * mu[d2] * F(up/d2, d2) % mod) % mod;
		}
		ret = (ret + 1ll * s * (n+1-x) % mod) % mod;
	}
	return 2ll * ret % mod;
}

int main ()
{
	scanf("%d%d%d%d%d", &n, &m, &l, &r, &mod); init();
	int Ans = ((solve(1ll*r*r)-solve(1ll*l*l-1)) % mod + mod) % mod;
	if(l <= 1 && 1 <= r) Ans = (Ans + ((2ll * n * m % mod + n) % mod + m) % mod) % mod;
	printf("%d\n", Ans);
}