【CF506E】Mr. Kitayuta's Gift dp转有限状态自动机+矩阵乘法

【CF506E】Mr. Kitayuta's Gift

题意：给你一个字符串s，你需要在s中插入n个字符（小写字母），每个字符可以被插在任意位置。问可以得到多少种本质不同的字符串，使得这个串是回文的。答案对10007取模。

$|s|\le 200,n\le 10^9$

题解：神题。

首先由于题目要求本质不同，所以我们为了防止重复，考虑从两边向中间不断复原回文串，如果新加入的字符与s两端（或一端）的字符相同，则匹配成功，继续匹配下一个字符。也就是说我们取的是s在回文串中最外面的出现位置。

为了方便，我们先只考虑n+|s|为偶数的情况，可以设出DP状态：设f[i][a][b]表示从外往里加入了i个字符，原串左边匹配到了a，有边匹配到了b的方案数。当新加入一个字符时，我们根据它是否与a和b匹配来确定转移到哪个状态。我们发现这个过程其实是在一个有限状态自动机上匹配的过程。对于s=abaac，转移的过程如下图：

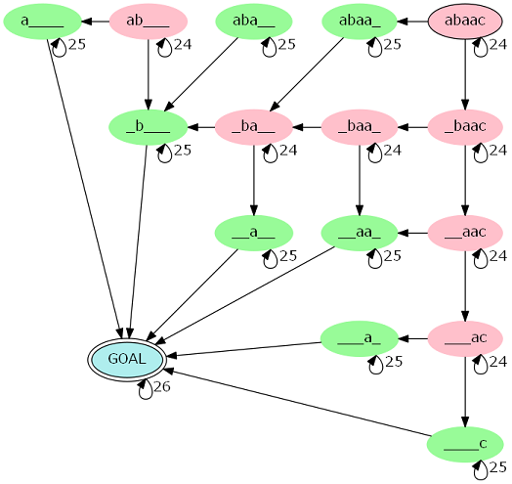
其中GOAL代表匹配完毕，它之后可以接任何字符，所以有26条自环。对于红点，它代表的状态两端的字符不相同，所以他有2条出边，24条自环。对于绿点，它代表的状态两端的字符相同，所以有1条出边和25条自环。特别地，能转移到GOAL的点都是绿点。

直接建出来这个自动机显然节点数目是$|s|^2$的，无法用矩乘优化。所以我们考虑对这个自动机进行压缩。可以发现，整个自动机其实可以被拆成若干条链，其中一条链上如果有i个红点，就有$\lceil {|s|-i\over 2}\rceil$个绿点。既然我们已经把自动机拆成链了，那么每条链上红点绿点的顺序也就无关紧要了，我们只需要知道每条链上红点与绿点的数目。换句话说，我们需要知道有多少条链有i个红点，这样一来本质不同的链就只有|s|条了。

统计方法比较简单，用g[a][b][i]表示在所有从起始节点走到(i,j)这个节点的路径中，有多少条已经走了i个红点。转移复杂度$|s|^3$。

既然我们已经有了|s|种链的各自数目，我们就可以想办法用$O(|s|)$个节点来构建一个新的自动机了。到这里我的方法和官方做法出现了分歧，个人认为我的做法比较简单。

构建|s|个红点串成一串，从起点指出来；$\lceil{|s|\over 2}\rceil$个绿点串成一串，指向终点。对于一种串$(i,\lceil {|s|-i\over 2}\rceil)$，我们从第i个红点向第$\lceil {|s|-i\over 2}\rceil$个绿点连一条边即可。这样一来点数就是${3\over 2}|s|$，可以用矩乘优化。如下图：

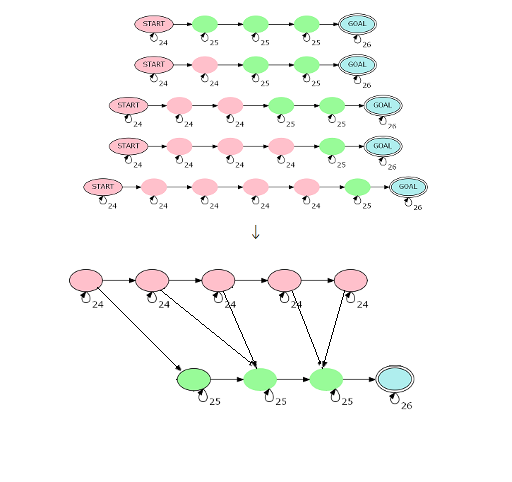
那么对于n+|s|为奇数的情况呢？我们先进行$n+|s|+1\over 2$步矩乘，但是在最后一步时形如(i,i+1)的绿点是不能直接转移到终点的。于是我们要将这些转移的贡献减去，方法是将(i,i+1)这样的点设为终点（无自环），重新建图跑一边矩乘即可。

本题的矩乘优化常数小技巧：发现我们只能从编号小的点转移到编号大的点，所以j只需要从i枚举到n，k只需要从i枚举到j即可。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int P=10007;
int n,m,N;
int f[210][210][210],g[210];
struct M
{
	int v[310][310];
	int * operator [] (const int &a) {return v[a];}
	M () {memset(v,0,sizeof(v));}
	inline M operator * (const M &a) const
	{
		M b;
		int i,j,k;
		for(i=0;i<=N;i++)	for(j=i;j<=N;j++)	for(k=i;k<=j;k++)	b.v[i][j]=(b.v[i][j]+v[i][k]*a.v[k][j])%P;
		return b;
	}

}S,T;
char str[210];
inline void pm(int y)
{
	while(y)
	{
		if(y&1)	S=S*T;
		T=T*T,y>>=1;
	}
}
int main()
{
	scanf("%s%d",str,&m),n=strlen(str);
	int i,j,k;
	f[0][n-1][0]=1;
	for(i=0;i<n;i++)
	{
		for(j=n-1;j>=i;j--)
		{
			if(str[i]==str[j])
			{
				for(k=0;k<i+n-j;k++)
				{
					if(i+1<j)	f[i+1][j-1][k]=(f[i+1][j-1][k]+f[i][j][k])%P;
					else	g[k]=(g[k]+f[i][j][k])%P;
				}
			}
			else
			{
				for(k=0;k<i+n-j;k++)
				{
					f[i+1][j][k+1]=(f[i+1][j][k+1]+f[i][j][k])%P;
					f[i][j-1][k+1]=(f[i][j-1][k+1]+f[i][j][k])%P;
				}
			}
		}
	}
	N=n+(n+1)/2+1;
	S[0][1]=1,S[0][N-(n+1)/2]=g[0],T[N][N]=26;
	for(i=1;i<=n;i++)
	{
		T[i][i]=24,T[i][N-(n-i+1)/2]=g[i];
		if(i!=n)	T[i][i+1]=1;
	}
	for(i=n+1;i<N;i++)	T[i][i+1]=1,T[i][i]=25;
	if((n+m)&1)
	{
		pm((n+m+1)>>1);
		int ans=S[0][N];
		memset(S.v,0,sizeof(S.v));
		memset(T.v,0,sizeof(T.v));
		memset(g,0,sizeof(g));
		for(i=0;i<n-1;i++)	if(str[i]==str[i+1])	for(k=0;k<=n;k++)
		{
			g[k]=(g[k]+f[i][i+1][k])%P;
		}
		S[0][1]=1,S[0][N-(n+1)/2]=g[0];
		for(i=1;i<=n;i++)
		{
			T[i][i]=24,T[i][N-(n-i+1)/2]=g[i];
			if(i!=n)	T[i][i+1]=1;
		}
		for(i=n+1;i<N;i++)	T[i][i+1]=1,T[i][i]=25;
		pm((n+m+1)>>1);
		printf("%d",(ans-S[0][N]+P)%P);
	}
	else
	{
		pm((n+m)>>1);
		printf("%d",S[0][N]);
	}
	return 0;
}//abaac 2