bzoj 4585 烟火表演 - 动态规划 - 可并堆

题目传送门

　　传送门I

　　传送门II

题目大意

　　给定一棵带边权有根树，修改一条边的边权的代价是修改前和修改后的值的绝对值之差。不能将一条边的边权改为负数。问使得根节点到所有叶节点的距离相等的最小代价。

　　当前正在考虑某个节点，设$f(x)$表示算上它到父节点的边，后将所有叶节点到它的父节点的距离改为$x$的最小代价。设$g(x)$表示将它所在的子树内的所有叶节点到它的距离改为$x$的最小代价，它和它父节点的边的边权为$w$。

　　对于一个点的各个子树之间互相独立，所以这个点的$g$函数相当于，它的各个子节点的$f$函数值的和。

$g(x) = \sum_{y\in son(x)}f_{y}(x)$

　　对于$f$函数，我们需要做决策：

$f(x) = \min_{0\leqslant y\leqslant x}\left \{ g(y) + \left | w - (x - y) \right | \right \}$

　　这等价于将每个位置$x$，考虑它前面位置的$g$函数值，和函数$h(y) = \left | w - (x - y) \right |$的和，然后取一个最小值作为$f(x)$。

　　于是就懵逼。值域可能很大，数组也开不下，所以怎么办呢？

　　考虑这个函数图像具有的性质。

　　首先考虑叶节点的$f$函数（它的$g$函数没有意义）。它是一条优美的绝对值函数的图像：

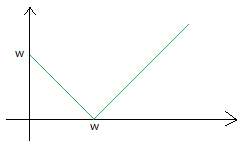
　　然后在考虑它的父节点，它的父节点的$g$函数将若干个这样的函数加在了一起。因为旧函数的导函数递增，新函数的导函数也等于旧函数导函数的和，所以新函数斜率递增。

　　而且这个函数图像非常特殊，每遇到一个拐点，导函数的值加1。

　　它的父节点的$g$函数可能会长成下面这个样子（这图画得很不标准）：

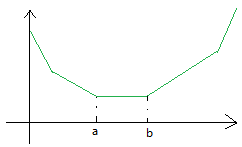
　　它一定会出现平着的一段区间$[a, b]$。然后分类讨论一下它变换到$f$函数。

　　当$0\leqslant x \leqslant a$时，显然$f(x)$的决策点取$x$最优。

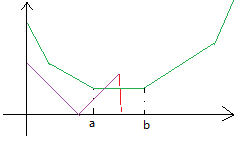
　　当$a < x \leqslant a + w$时，显然$f(x)$的决策点取$a$最优。

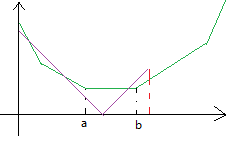
　　当$a + w < x \leqslant b + w$时，显然$f(x)$的最优决策点取$x - w$。

　　当$x > b + w$时，决策点取$b$。

　　所以整理一下式子不难得到：

$f(x) = \left\{\begin{matrix}g(x) + w \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (0\leqslant x \leqslant a)\\ g(a) + w - x + a \ (a < x \leqslant a + w)\\ g(x - w) \ \ \ \ \ \ (a + w < x \leqslant b + w)\\ g(b) + x - b - w \ \ \ \ \ \ \ (x > b + w)\end{matrix}\right.$

　　这有什么用呢？

　　考虑它的图像的变化：

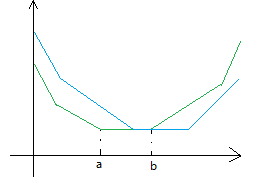
　　它相当于将平的一段向右移动了$w$个单位，然后将$[0, a]$的函数图像向上平移了$w$个单位，中间空的一段补斜率为-1的线段。

　　然后把$[b, +\infty )$的图像变成斜率为1的射线。

　　这样新函数的图像也是一个满足刚刚提到的两点性质的下凸壳，不难证明所有非叶节点的$f, g$函数都满足这样的性质。

　　因此，我们考虑用某个数据结构来维护拐点集合。

　　所以我们可以平衡树 + 启发式合并来做这道题。于是这样就被卡掉了。

　　所以怎么办呢？实际上，我并不需要维护一个完全有序的序列，我只要支持：

1. 弹掉最大的某几个。
2. 支持插入元素
3. 支持快速合并

　　因为被弹掉的元素一去不复返，可以暴力弹掉它们，因此可以想到可并堆。

　　这样时间复杂度降为$O((n + m)\log (n + m))$。

Code

 /**
  * bzoj
  * Problem#4585
  * Accepted
  * Time: 8736ms
  * Memory: 18872k
  */
 #include <iostream>
 #include <cassert>
 #include <cstdlib>
 #include <cstring>
 #include <cstdio>
 #ifndef WIN32
 #define Auto "%lld"
 #else
 #define Auto "%I64d"
 #endif
 using namespace std;
 typedef bool boolean;

 #define ll long long
 const int N = 6e5 + ;

 typedef class SkewNode {
     public:
         ll val;
         SkewNode *l, *r;

         SkewNode()    {    }
 }SkewNode;

 SkewNode pool[N];
 SkewNode* top = pool;

 SkewNode* newnode(int val) {
     top->val = val;
     return top++;
 }

 SkewNode* merge(SkewNode* a, SkewNode* b) {
     if (!a || !b)    return (a) ? (a) : (b);
     if (a->val < b->val)    swap(a, b);
     a->r = merge(a->r, b);
     swap(a->l, a->r);
     return a;
 }

 int n, m;
 int *fa, *cs, *ss, *ks;
 ll *bs;
 SkewNode** rs;

 inline void init() {
     scanf("%d%d", &n, &m);
     n += m;
     bs = new ll[(n + )];
     fa = new int[(n + )];
     cs = new int[(n + )];
     ss = new int[(n + )];
     ks = new int[(n + )];
     rs = new SkewNode*[(n + )];
     memset(bs, , sizeof(ll) * (n + ));
     memset(ks, , sizeof(int) * (n + ));
     memset(ss, , sizeof(int) * (n + ));
     memset(rs, , sizeof(SkewNode*) * (n + ));
     for (int i = ; i <= n; i++)
         scanf("%d%d", fa + i, cs + i);
 }

 inline void solve() {
     for (int i = n - m + ; i <= n; i++) {
         int f = fa[i];
         ss[f] += , ks[f] += , bs[f] += cs[i];
         rs[f] = merge(rs[f], newnode(cs[i]));
         rs[f] = merge(rs[f], newnode(cs[i]));
     }
     for (int i = n - m; i > ; i--) {
         while (ss[i] > ks[i] + )    ss[i]--, rs[i] = merge(rs[i]->l, rs[i]->r);
         SkewNode *a = rs[i], *b = rs[i] = merge(rs[i]->l, rs[i]->r);
         bs[i] += cs[i], a->val += cs[i], b->val += cs[i], a->l = a->r = NULL;
         rs[i] = merge(rs[i], a);
         int f = fa[i];
         bs[f] += bs[i], ks[f] += ks[i], ss[f] += ss[i];
         rs[f] = merge(rs[f], rs[i]);
     }
     while (ss[] > ks[])    ss[]--, rs[] = merge(rs[]->l, rs[]->r);
     ll res = bs[];
     while (rs[])
         res -= rs[]->val, rs[] = merge(rs[]->l, rs[]->r);
     printf(Auto"\n", res);
 }

 int main() {
     init();
     solve();
     return ;
 }