1、设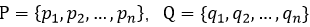是两组Rd空间的点集，可根据这两个点集计算它们之间的旋转平移信息。

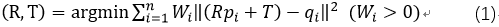
2、设R为不变量，对T求导得：

令

则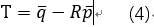

将(4)带入(1)得：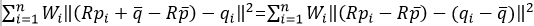

令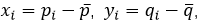

则

(相当于对原来点集做减中心点预处理，再求旋转量)

3、 计算旋转量

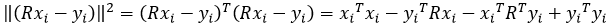
因为R为正交阵且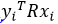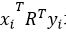，均为标量，

所以

所以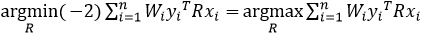

而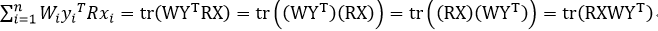

令，对S进行SVD分解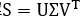，则

令，则M为正交阵，

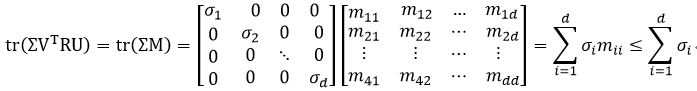
要求得最大迹，则使mii=1,则M必为单位阵，即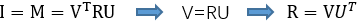

SVD分解求解旋转矩阵的更多相关文章

  1. SVD分解技术详解

    版权声明: 本文由LeftNotEasy发布于http://leftnoteasy.cnblogs.com, 本文可以被全部的转载或者部分使用,但请注明出处,如果有问题,请联系wheeleast@gm ...

  2. SVD分解　解齐次线性方程组

    SVD分解 只有非方阵才能进行奇异值分解 SVD分解:把矩阵分解为 特征向量矩阵+缩放矩阵+旋转矩阵 定义 设\(A∈R^{m×n}\),且$ rank(A) = r (r > 0) $,则矩阵 ...

  3. 机器学习之SVD分解

    一.SVD奇异值分解的定义 假设是一个的矩阵,如果存在一个分解: 其中为的酉矩阵,为的半正定对角矩阵,为的共轭转置矩阵,且为的酉矩阵.这样的分解称为的奇异值分解,对角线上的元素称为奇异值,称为左奇异矩 ...

  4. 矩阵的SVD分解

    转自 http://blog.csdn.net/zhongkejingwang/article/details/43053513(实在受不了CSDN的广告) 在网上看到有很多文章介绍SVD的,讲的也都 ...

  5. SVD分解及线性最小二乘问题

    这部分矩阵运算的知识是三维重建的数据基础. 矩阵分解 求解线性方程组:,其解可以表示为. 为了提高运算速度,节约存储空间,通常会采用矩阵分解的方案,常见的矩阵分解有LU分解.QR分解.Cholesky ...

  6. 机器学习Python实现 SVD 分解

    这篇文章主要是结合机器学习实战将推荐算法和SVD进行对应的结合 不论什么一个矩阵都能够分解为SVD的形式 事实上SVD意义就是利用特征空间的转换进行数据的映射,后面将专门介绍SVD的基础概念.先给出p ...

  7. SVD分解

    首先,有y = AX,将A看作是对X的线性变换 但是,如果有AX = λX,也就是,A对X的线性变换,就是令X的长度为原来的λ倍数. *说起线性变换,A肯定要是方阵,而且各列线性无关.(回想一下,A各 ...

  8. SVD分解的理解[转载]

    http://www.bfcat.com/index.php/2012/03/svd-tutorial/ SVD分解(奇异值分解),本应是本科生就掌握的方法,然而却经常被忽视.实际上,SVD分解不但很 ...

  9. 机器学习中的矩阵方法04：SVD 分解

    前面我们讲了 QR 分解有一些优良的特性,但是 QR 分解仅仅是对矩阵的行进行操作(左乘一个酉矩阵),可以得到列空间.这一小节的 SVD 分解则是将行与列同等看待,既左乘酉矩阵,又右乘酉矩阵,可以得出 ...

随机推荐

  1. burpsuite拦截https数据包（Firefox）

    1.配置浏览器对http/https都使用burpsuite代理 http和https是分开的,对http使用了代理并不代表对https也使用了代理,要配置浏览器让其对https也使用同样的代理. 当 ...

  2. Mysql设置自增字段的方法

    #int : 字段类型 alter table 表名 modify 字段名 int auto_increment primary key

  3. ASP.Net MVC(1) 之走进MVC

    一.MVC三层架构: mvc三层架构,大家都比较熟悉了,这里再介绍一下.Mvc将应用程序分离为三个部分: Model:是一组类,用来描述被处理的数据,同时也定义这些数据如何被变更和操作的业务规则.与数 ...

  4. laravel 查询指定字段的值

    $this->model->where('id',$id)->value('user');

  5. learning at command AT+CEREG

    AT command AT+CEREG [Purpose]        Learning how to query the network registration status   [Eeviro ...

  6. centos7 克隆 网卡无法启用

    1.克隆后查看网卡无法启用,报错信息如下: Apr :: agent systemd: network.service: control process exited, code=exited sta ...

  7. commons-logging,log4j和jdklog的调用方式

    commons-logging包含log4j和jdklog. commons-logging: Log log= LogFactory.getLog(getClass());//commons log ...

  8. Oracle 12c的自增列Identity Columns

    在Oracle的12c版本中,Oracle实现了类似MySQL中的auto_increment的自增列,下面我们看一起Oracle是怎么实现的. Oracle Database 12c Enterpr ...

  9. 将excel数据分块多线程导入

    参考链接:http://blog.csdn.net/liqi_q/article/details/53032027

  10. 深入理解java虚拟机---虚拟机工具jps与jstat(十四)

    jps-java process status jps类似于linux的ps命令,用于查看进程. JPS 名称: jps - Java Virtual Machine Process Status T ...