清明 DAY 1

数学基础

 

Part 1.  高精度计算

 

---

 

Part 2.  模意义下的运算

           

        mod 

对一个数取模，其实就是取余数

 

注意：

•   无除法运算

•   满足基本的交换律、分配率、结合律

•   对中间结果取模不影响最终答案

 

---

 

Part 3.  快速幂

 

---

 

Part 4.  费马小定理与GCD&LCM

 

---

 

Part 5.  素数与筛法

 

---

 

Part 6.  欧拉函数

 

---

矩阵

 

高斯消元

 

 

 行列式

 

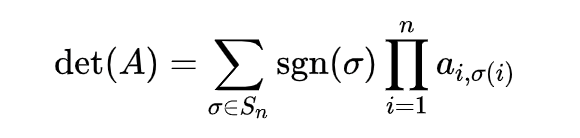
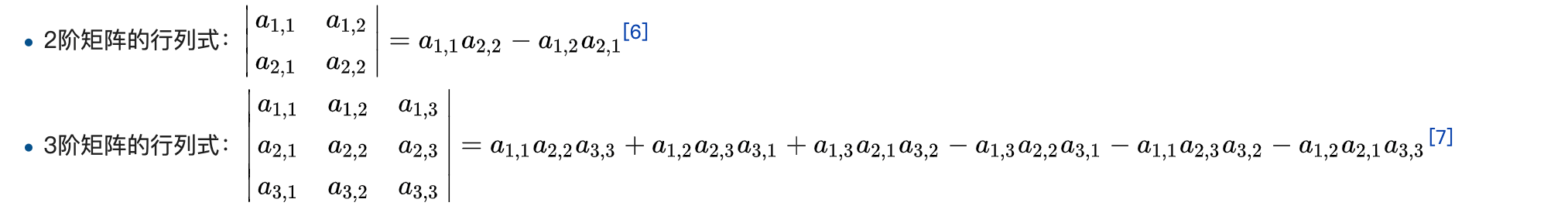
行列式计算：

1.利用高斯消元将原矩阵变为对角矩阵

2.将对角线上的值连乘得到行列式

 

矩阵逆元

P4783 【模板】矩阵求逆

逆元的定义：

     若矩阵B*A=I 则称B为A的左逆元

     若矩阵A*B=I 则称B为A的左逆元

 

有逆元的前提：

     矩阵行列式不为0

 

 LH的矩阵求逆板子：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define LL long long
#define N 405
using namespace std;
const int mod=1e9+7;

template<class T>inline void rd(T &x){
    x=0; short f=1; char c=getchar();
    while(c<'0' || c>'9') f=c=='-'?-1:1,c=getchar();
    while(c<='9' && c>='0') x=x*10+c-'0',c=getchar();
    x*=f;
}

int n,m;
int f[N][N<<1],r,ans;

inline int qpow(int x,int k){
    int ret=1;
    while(k){
        if(k&1) ret=1LL*ret*x%mod;
        x=1LL*x*x%mod; k>>=1;
    } return ret;
}

inline void Gauss(){
    for(int i=1;i<=n;i++){
        for(int j=i;j<=n;j++)
            if(f[j][i]){
                if(j!=i) for(int k=1;k<=m;k++) swap(f[i][k],f[j][k]);
                break;
            }
        if(!f[i][i]){puts("No Solution");exit(0);}
        r=qpow(f[i][i],mod-2);
        for(int j=i;j<=m;j++) f[i][j]=1LL*f[i][j]*r%mod;
        for(int j=1;j<=n;j++)
            if(j!=i){
                r=f[j][i];
                for(int k=i;k<=m;k++)
                    f[j][k]=(f[j][k]-1LL*r*f[i][k]%mod+mod)%mod;
            }
    }
    for(int i=1;i<=n;i++){
        for(int j=n+1;j<=m;j++) printf("%d ",f[i][j]);
        puts("");
    } return;
}

int main(){
    rd(n); m=n<<1;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++) rd(f[i][j]);
        f[i][n+i]=1;
    }
    Gauss();
    return 0;
}

 

---

 

扩充知识

然而后面这些知识点LH貌似没讲

矩阵树定理

 

一个图的邻接矩阵G：对于无向图的边(u,v)，G[u][v]++,G[v][u]++

一个图的度数矩阵D：对于无向图的边(u,v)，D[u][u]++,D[v][v]++

而通过这两个矩阵就可以构造出图G的基尔霍夫矩阵：C=D-G.

 

 Matrix Tree定理：

      将图G的基尔霍夫矩阵去掉第i行和第i列(i可以取任意值，可以证明所得到的结果相同)，得到(n-1)*(n-1)的矩阵，对这个矩阵进行行列式的值求解，abs(det(A))即为图G的生成树个数。

 

 

 

 

有向图 - 矩阵树定理

 

树形图：以i点为根节点的树形图有(n-1)条边，从i节点出发可以到达其他所有(n-1)个节点.

 

定义： 有向图的邻接矩阵G：对于有向图的边(u,v)，G[u][v]++.

            有向图的度数矩阵D：对于有向图的边(u,v)，D[v][v]++.

 

尤其需要注意的是：有向图的度数矩阵指的是一个点的入度，而不是出度。

而有向图的基尔霍夫矩阵的构造方式是一模一样的：C=D-G.

 

有向图Matrix Tree定理：

        将有向图G的基尔霍夫矩阵去掉第i行和第i列，得到(n-1)*(n-1)的矩阵，对这个矩阵进行行列式的值求解，abs(det(A))就是以i为根的树形图的个数。

 

 

 

拓展：k^2logn求常系数线性递推方程

• f(n) = a0 + a1*f(n-1) + … + ak*f(n-k)

• 给出 f(1) ~ f(k)， 求 f(n) % p

 

 

 

 

POJ 3735

 

 

洛谷2233 公交车线路

 

 题解：