BZOJ_1005_ [HNOI2008]_明明的烦恼_(组合数学+purfer_sequence+高精度+分解因数+快速幂)

描述

---

http://www.lydsy.com/JudgeOnline/problem.php?id=1005

一棵树有n个点,给出没给节点的度,如果没有限制则为-1,求共有多少种可能的树.

分析

---

蒟蒻我肯定是不会做的,所以先来抄一段题解...

---

这题需要了解一种数列： Purfer Sequence

我们知道，一棵树可以用括号序列来表示，但是，一棵顶点标号（1~n）的树，还可以用一个叫做 Purfer Sequence 的数列表示

一个含有 n 个节点的 Purfer Sequence 有 n-2 个数，Purfer Sequence 中的每个数是 1~n 中的一个数

一个定理：一个 Purfer Sequence 和一棵树一一对应

先看看怎么由一个树得到 Purfer Sequence

由 一棵树得到它的 Purfer Sequence 总共需要 n-2 步，每一步都在当前的树中寻找具有最小标号的叶子节点（度为 1），将与其相连的点的标号设为 Purfer Sequence 的第 i 个元素，并将此叶子节点从树中删除，直到最后得到一个长度为 n-2 的 Purfer Sequence 和一个只有两个节点的树

看看下面的例子：

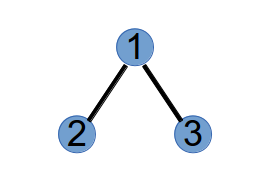
假设有一颗树有 5 个节点，四条边依次为：(1, 2), (1, 3), (2, 4), (2, 5)，如下图所示：

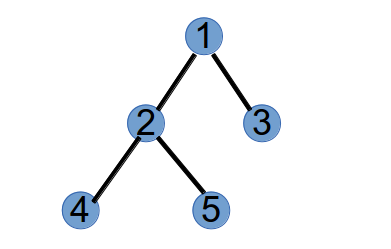
第 1 步，选取具有最小标号的叶子节点 3，将与它相连的点 1 作为第 1 个 Purfer Number，并从树中删掉节点 3：

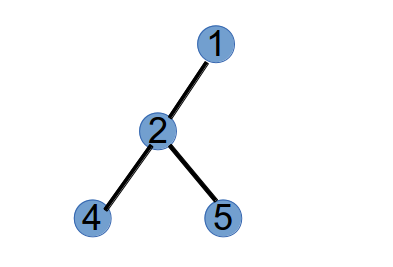
第 2 步，选取最小标号的叶子节点 1，将与其相连的点 2 作为第 2 个 Purfer Number，并从树中删掉点 1：

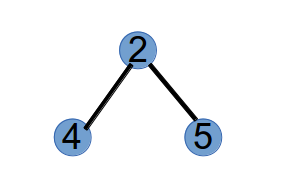
第 3 步，选取最小标号的叶子节点 4，将与其相连的点 2 作为第 3 个 Purfer Number，并从树中删掉点 4：

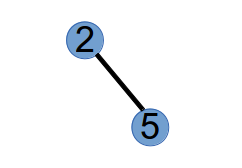
最后，我们得到的 Purfer Sequence 为：1 2 2

不难看出，上面的步骤得到的 Purfer Sequence 具有唯一性，也就是说，一个树，只能得到一个唯一的 Purfer Sequence

接下来看，怎么由一个 Purfer Sequence 得到一个树

由 Purfer Sequence 得到一棵树，先将所有编号为 1 到 n 的点的度赋初值为 1，然后加上它在 Purfer Sequence 中出现的次数，得到每个点的度

先执行 n-2 步，每一步，选取具有最小标号的度为 1 的点 u 与 Purfer Sequence 中的第 i 个数 v 表示的顶点相连，得到树中的一条边，并将 u 和 v 的度减一

最后再把剩下的两个度为 1 的点连边，加入到树中

我们可以根据上面的例子得到的 Purfer Sequence ：1 2 2 重新得到一棵树

Purfer Sequence 中共有 3 个数，可以知道，它表示的树中共有 5 个点，按照上面的方法计算他们的度为下表所示：

顶点	1	2	3	4	5
度	2	3	1	1	1

第 1 次执行，选取最小标号度为 1 的点 3 和 Purfer Sequence 中的第 1 个数 1 连边：

将 1 和 3 的度分别减一：

顶点	1	2	3	4	5
度	1	3	0	1	1

第 2 次执行，选取最小标号度为 1 的点 1 和 Purfer Sequence 中的第 2 个数 2 连边：

将 1 和 2 的度分别减一：

顶点	1	2	3	4	5
度	0	2	0	1	1

第 3 次执行，将最小标号度为 1 的点 4 和 Purfer Sequence 第 3 个数 2 连边：

将 2 和 4 的度分别减一：

顶点	1	2	3	4	5
度	0	1	0	0	1

最后，还剩下两个点 2 和 5 的度为 1，连边：

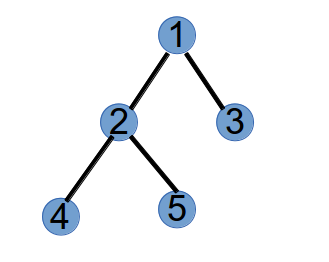
至此，一个 Purfer Sequence 得到的树画出来了，由上面的步骤可知，Purfer Sequence 和一个树唯一对应

综上，一个 Purfer Sequence 和一棵树一一对应

那么其数只要求出来合法的purfer sequence的数量就是生成树的数量。

将树转化为prufer编码：

n为树的节点数，d[i]为各节点的度数，(注意计算tot的时候只计算d[i]!=-1的数）m为无限制度数的节点数。

则            

所以要求在n-2大小的数组中插入tot各序号，共有种插法；

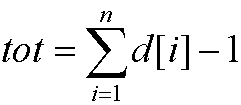
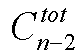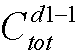在tot各序号排列中，插第一个节点的方法有种插法； 
 插第二个节点的方法有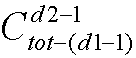种插法；………

另外还有m各节点无度数限制，所以它们可任意排列在剩余的n-2-tot的空间中，排列方法总数为；

 

根据乘法原理：

 

 

然后就要高精度了…..但高精度除法太麻烦了，显而易见的排列组合一定是整数，所以可以进行质因数分解，再做一下相加减。

---

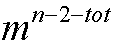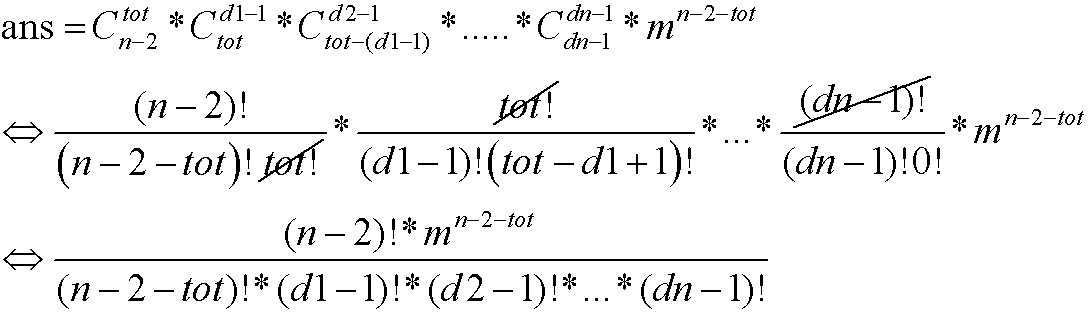
基本上知道什么是purfer_sequence这道题就没问题了.然后就是组合数学的推导.由于要用高精度,除法不太方便,我是直接暴力分解因数,然后坐指数相加减...最后来一发快速幂.

p.s.

1.按理来说应该要特判无解的情况,但是没有特判也A了...

 #include <bits/stdc++.h>
 using namespace std;

 const int maxn=+,maxl=,base=;
 int n,cnt,sum;
 int s[maxn],c[maxn];
 typedef long long ll;

 struct Bign{
     int cnt; ll x[maxl];
     Bign(int t=){
         memset(x,,sizeof x);
         x[cnt=]=t;
     }
     ll & operator [](int id){ return x[id]; }
 }ans();
 Bign operator *= (Bign &x,Bign &y){
     Bign z;
     for(int i=;i<=x.cnt;i++)for(int j=;j<=y.cnt;j++)
         z[i+j-]+=x[i]*y[j], z[i+j]+=z[i+j-]/base, z[i+j-]%=base;
     z.cnt=x.cnt+y.cnt;
     if(!z[z.cnt]) z.cnt--;
     x=z;
 }
 ostream & operator << (ostream &out,Bign &x){
     printf("%lld",x[x.cnt]);
     for(int i=x.cnt-;i;i--) printf("%08lld",x[i]);
     return out;
 }
 void decomposition(int x,int y){
     for(int i=;i*i<=x;i++)while(x%i==) c[i]+=y, x/=i;
     if(x^) c[x]+=y;
 }
 void quick_power(int i,int y){
     Bign x(i);
     for(;y;x*=x, y>>=) if(y&) ans*=x;
 }
 int main(){
     freopen("bzoj_1005.in","r",stdin);
     freopen("bzoj_1005.out","w",stdout);
     scanf("%d",&n);
     for(int i=;i<=n;i++){
         int t; scanf("%d",&t);
         if(t>) s[++cnt]=t-, sum+=t-;
     }
     for(int i=;i<=n-;i++) decomposition(i,);
     for(int i=;i<=cnt;i++)for(int j=;j<=s[i];j++) decomposition(j,-);
     for(int i=;i<=n--sum;i++) decomposition(i,-);
     decomposition(n-cnt,n--sum);
     for(int i=;i<=n;i++)if(c[i]) quick_power(i,c[i]);
     cout<<ans<<endl;
     return ;
 }

1005: [HNOI2008]明明的烦恼

Time Limit: 1 Sec  Memory Limit: 162 MB
Submit: 3980  Solved: 1583
[Submit][Status][Discuss]

Description

　　自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?

Input

　　第一行为N(0 < N < = 1000),
接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1

Output

　　一个整数,表示不同的满足要求的树的个数,无解输出0

Sample Input

3
1
-1
-1

Sample Output

2

HINT

　　两棵树分别为1-2-3;1-3-2

Source