VOLO论文笔记

Outlook Attention

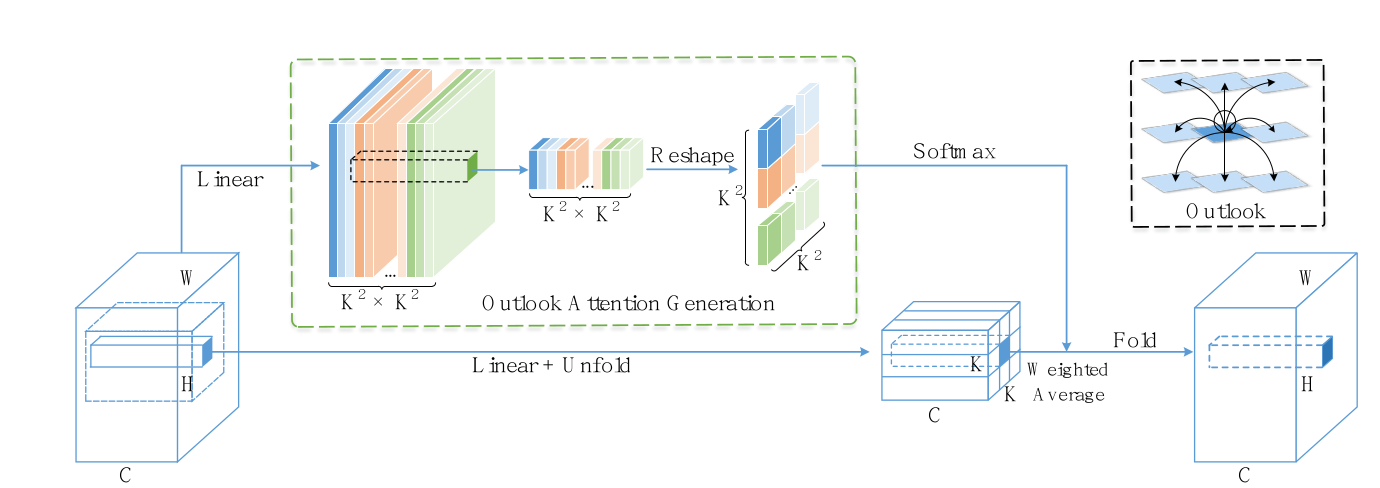
设给定输入为 \(X \in R^{H \times W \times C}\), 首先经过两个线性映射得到两个输出A 和 V，A叫做outlook weight \(A \in R^{H \times W \times K^4}\), V叫做value representation \(V \in R^{H \times W \times C}\). A对应下图绿色虚线框中左侧图形，直观上通道数由C变成了\(K^4\); V是图片中第二排中间那张图形。

outlook attention 模块是考虑\(K \times K\)区域内每个空间位置特征间关系。A经过reshape 得到尺寸为\(R^{H \times W \times K^2 \times K^2}\) ,其中每个空间位置值代表对应原始输入X对应空间位置点的局部\(K \times K\)区域内各个空间点特征之间两两相关性度量，由于区域有\(K^2\)个空间位置点，因此相关度量矩阵是\(R^{K^2 \times K^2}\)

attn = nn.Linear(C, k ** 4)
a = attn(x).reshape(H*W, K*K, K*K)

上述代码即表示绿色虚线框生成过程

v_pj = nn.Linear(C, C)
unfold = nn.Unfold(K, padding)
v = v_pj(x).permute(2, 1, 0)
v = unfold(v).reshape(C, K*K, H*W).permute(2, 1, 0)

上述代码块就是公式3 。是将特征V （value representation ）使用\(K \times K\)在其上滑动时，同一平面内特征展开，不同平面特征依次拼接在其后；再将空间X-方向和Y-方向展开成一条。Unfold操作可以参考下面连接理解。可以理解为将原始特征X的局部区域\(K \times K\)内特征平铺开来。由于Unfold操作stride=1，因此unfold(v)的形状为\(R^{CK^2 \times HW}\)

a = a.softmax(dim=-1)
x = mul(a, v).permute(2, 1, 0).reshape(C*K*K, H*W)

此处的\(a \in R^{K^2 \times K^2}, v \in R^{K^2 \times C}\) ，忽略HW。\(a \in R^{K^2 \times K^2}\) 表示某个位置局部区域各个位置点与本区域内其它位置的特征相似性度量，而$v \in R^{K2 \times C} $ 表示这个区域的特征，每个位置点的特征长度为C，有 \(K^2\) 个位置，因此二者相乘，每个位置点第i个通道处的特征值是该通道对应的\(K \times K\)区域内特征值的加权平均。

回到最开始关于Outlook Attention初衷/思考：

• 每个空间位置的特征具有足够的代表性，可以生成注意力权重，用于局部聚合其相邻的特征
• 密集和局部的空间聚合可以有效地编码更精细信息

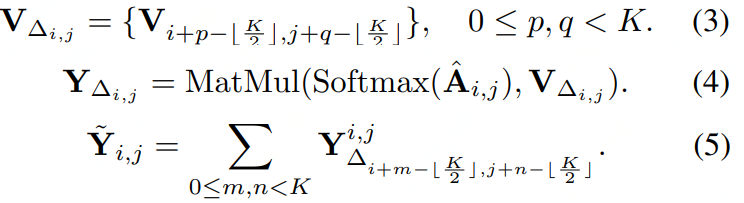
参考

[1] Fold/Unfold 操作详解 https://blog.csdn.net/ViatorSun/article/details/119940759