Network Science：巴拉巴西网络科学学习笔记3—

第二章：随机网络Erdős-Rényi Network （ER网络）

随机网络的两种定义形式：

$G(N,L)$模型：N个节点，L条边随机链接。

$G(N,p)$模型：N个节点，每个节点之间以p的概率连接。

随机网络恰好有L条链接的概率为：即 1）2）3）的乘积。是一个二项分布，所以二项分布的均值，矩，二阶矩等都很常用。

1）L个点对之间存在链接的概率 2）剩余$N(N-1)/2 -L$ 个点对之间没有链接的概率 3）在所有点对中选择L个点对放置链接的选择方式。

\[p_L= {\frac{N(N-1)}{2} \choose L}p^L(1-p)^{\frac{N(N-1)}{2}-L}
\]

显然，我们能够算出期望链接数$<L>=p\frac{N(N-1)}{2}$, 平均度 $<k>=p(N-1)$

度分布：$p_k$一个节点$i$有$k$个链接的概率。

对ER图而言，

\[p_k={N-1 \choose k}p^k(1-p)^{N-1-k}
\]

即ER图的度分布服从二项分布。（在$N\gg <k>$时，二项分布可以近似为泊松分布，它们的性质类似，但是二项分布有两个参数，泊松分布只有一个参数）

注意：大部分真实网络是稀疏的，所以网络的平均度远小于网络大小，即$N\gg <k>$。

即

\[p_k=e^{-<k>}\frac{{<k>}^k}{k!}
\]

由此，因为泊松分布不依赖于N，所以平均度相同但规模大小不同的随机网络的度分布几乎一样。

所以在大多数时候，我们使用泊松形式来刻画随机网络的度分布。

真实的网络不是泊松分布

事实上，在大的随机网络中，大多数节点的度分布在附近的狭窄范围内。随着k的增大，在ER图中观测到枢纽节点的概率比指数下降还快。

真实网络和随机网络的差异：

泊松分布低估了大度节点的个数。
真实网络中度的分布范围比随机网络中所预计的要宽得多。

随机网络的演化

考虑一个动态过程，从N个独立节点开始，链接被逐个放置在随机两个点之间。这一过程等价于逐渐增加p值。在p增加到一定程度时，巨连通块出现，其条件为$<k>=1$.由此，网络越大，形成巨连通块所需的p就越小。（巨连通块：giant component）

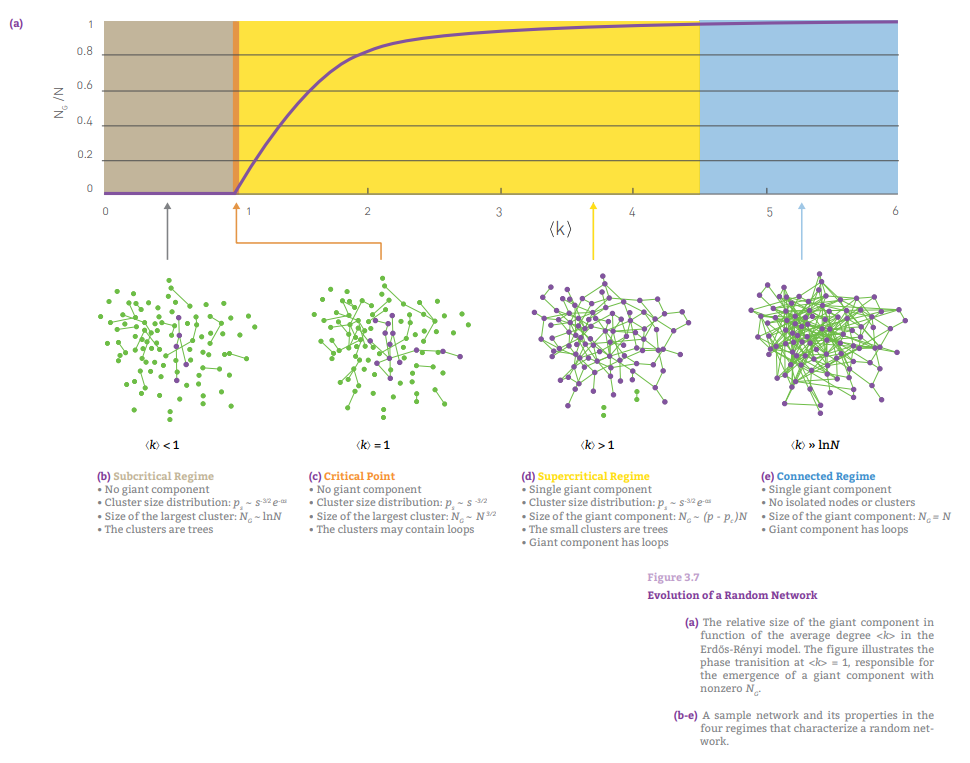
上面这图详细的表现了随着的增大，巨联通块的变化。

注意在临界点状态的网络有很多性质和处于相变状态的物理系统的性质相似。（为什么会发生这样的改变呢？？？？！！！！）

不同子图在随即图中的出现存在阈值概率。

真实网络是超临界的

随机网络理论对真实网络的两个预测：

当平均度达到=1后，巨联通块会出现，在超过1后节点才能自组织成一个网络。
当$<k>> lnN$ 时，所有联通块都被巨连通块吸收，从而形成一个联通网络。

小世界网络

随机网络的直径为：

\[d_{max} \approx \frac{lnN}{ln<k>}
\]

小世界性质一般定义为：

\[<d> \approx \frac{lnN}{ln<k>}
\]

当$d><d>$时，和起始节点距离为d的节点数迅速减少。

集聚系数

随机网络中局部集聚系数为：

\[C_i=\frac{<k>}{N}
\]

这个公式给出了两个预测：

在给定的情况下，网络越大，节点的集聚系数越小
在随机网络中，节点的局部集聚系数和节点的度相互独立。

但是真实网络和预测2中描述的不符。随机网络不能刻画真实网络的集聚特性。在具有同样的N和L的情况下，真实网络的集聚系数比随机网络预测的集聚系数高得多。

WATTS-STROGATZ MODEL 解决了高集聚系数和小世界性质共存的问题。

小结：真实的网络不是随机的

定量的来判断随机网络能在多大程度上刻画真实网络：

1）度分布 2）连通性 3）平均路径长度（小世界现象） 4）集聚系数

度分布：真实系统中，大度节点的数量要比随机网络模型预测的多得多。
连通性：根据随机网络的预测，在网络满足$<k> > 1$但不满足$<k> > lnN$的条件时除了巨联通块，还包含一些独立的小联通块，而大多数真实的网络中不包含独立的小连通块。
平均路径长度：随机网络有不错的近似，能解释小世界现象。
集聚系数：随机网络中，局部集聚系数和节点的度无关，以1/N 依赖于网络大小N，但是真实网络中C(k) 随着节点度的增大而减小，且与网络大小基本无关。

WATTS-STROGATZ MODEL 解决了高集聚系数和小世界性质共存的问题，但没法解释度分布和C(k)。

随机网络的指南作用

每当观测到某种网络性质时，我们都会问，该性质是否只是偶然出现的。为此，我们可以使用随机网络模型作为指南：如果该性质在随机网络中存在，则意味着它可以用随机性解释。如果该性质在随机网络中不存在，则它很有可能标志着某种秩序——需要更深入的解释。

最大度和最小度

网络的自然上界$k_{max}$，使得网络中最多只有一个节点的度大于$k_{max}$，数学上着意味着$k>k_{max}$的区域面积应该趋于0.

小世界的修正