多目标优化经典算法——NSGA-II
参考博客链接
https://blog.csdn.net/qq_35414569/article/details/79639848?utm_medium=distribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-0.no_search_link&spm=1001.2101.3001.4242
因为NSGA-II算法是一种遗传算法,所以首先搞清楚遗传算法的流程。
遗传算法流程
一般遗传算法的流程:
- 种群初始化
- 计算每个个体的适应度
- 选择
- 交叉
- 变异
根据是否满足解的精度要求和迭代次数来判断是否进行下一轮的遗传进化。
NSGA算法存在的3个问题
- O(MN^3)计算时间复杂度(其中M代表目标个数,N代表种群个数)
- 非精英机制方法
- 需要指定一个共享参数
NSGA-II算法
NSGA-II算法主要由以下三个部分组成
A、快速非支配排序方法
B、拥挤比较算子
C、主程序
A、快速非支配排序方法
- 传统排序方法:时间复杂度O(MN3),M是目标个数,N是种群个数。为了计算第一非支配前沿面,需要判断每个解和种群中的其他解的支配关系。一个解和其他解的支配关系需要O(MN)复杂度,每个解和其他解的支配关系需要O(MN2)复杂度。最坏的情况,N个解各自构成一个前沿面,时间复杂度就是O(MN3)。
- 快速非支配排序方法:首先需要计算两个变量 1)支配计数np,即支配解p的解的数量。2)Sp,即解p支配的解的集合。

如上图所示,对解c而言,解c被a,b两个解支配,所以nc为2。对解b而言,解b支配c,d,e,所以Sb={c,d,e}。
算法流程如下:

首先计算每个解的np和Sp,这需要O(MN2)时间复杂度,同时得到了第一前沿面
F
1
\mathcal{F1}
F1。第二部分就是计算其余的前沿面,需要遍历前沿面中的每个解以及这个解的Sp集合,将对应解p的np值减一,如果np值减为0了,就加入下一前沿面集合,这部分需要O(N2)时间复杂度。由于第一部分和第二部分是分开的,所以总的时间复杂度是O(MN2)。
B、拥挤比较算子
密度估计:对同一前沿面的解按照目标函数值排序,计算每个解在该目标函数下两侧解的目标函数归一化差值,然后将所有目标函数下的分量累加作为拥挤系数。
具体算法流程如下: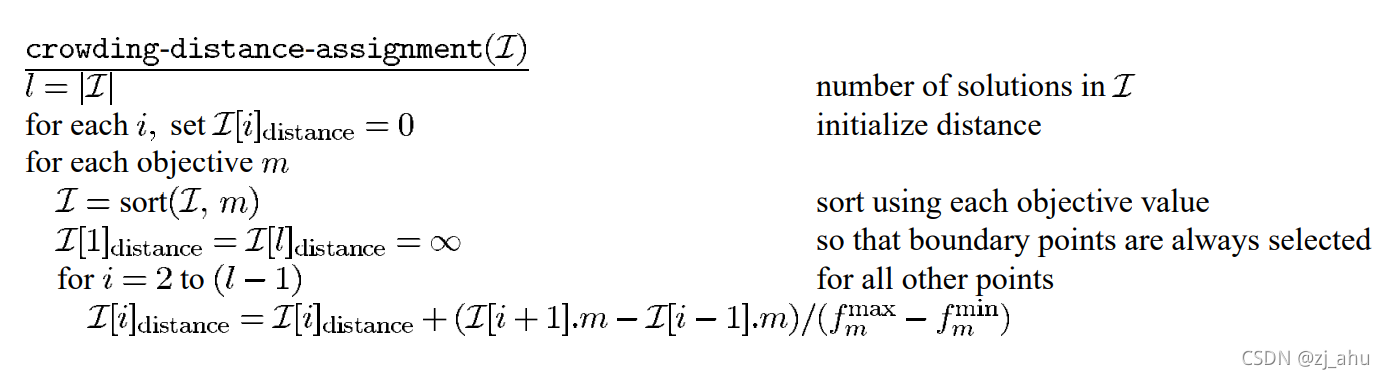
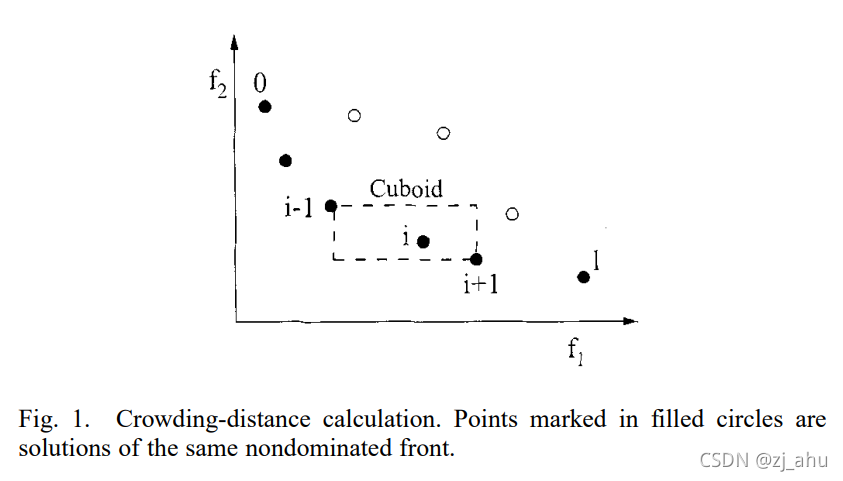
如图所示,直观上看,解i的拥挤系数就是虚线矩形周长的一半。
C、主程序
- 种群初始化:随机创建父代种群P0 ,为父代种群利用快速非支配排序算法计算出非支配等级,并利用二进制锦标赛机制重组以及变异算子生成大小为N的子代种群。
- 子代个体选择
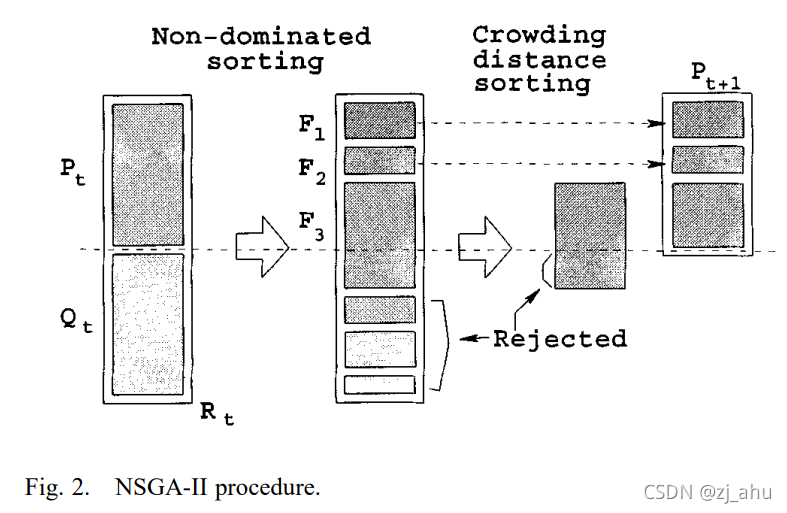
代码实现
参考博客链接
https://www.omegaxyz.com/2017/05/04/nsga2matlabzdt1/
主体代码是这篇博客的,仅将非支配排序部分修改为了原始论文中的
%% NSGA-II算法
clear; close all; clc; tic;
%% 初始化/参数设定
generations=100; %迭代次数
popnum=100; %种群大小(须为偶数)
poplength=30; %个体长度
minvalue=repmat(zeros(1,poplength),popnum,1); %个体最小值
maxvalue=repmat(ones(1,poplength),popnum,1); %个体最大值
%% 随机创建父代种群
population=rand(popnum,poplength).*(maxvalue-minvalue)+minvalue; %产生新的初始种群
%% 开始迭代进化
for gene=1:generations %开始迭代
%% 交叉
newpopulation=zeros(popnum,poplength); %子代种群
for i=1:popnum/2 %交叉产生子代
k=randperm(popnum); %从种群中随机选出两个父母,不采用二进制联赛方法
beta=(-1).^round(rand(1,poplength)).*abs(randn(1,poplength))*1.481; %采用正态分布交叉产生两个子代
newpopulation(i*2-1,:)=(population(k(1),:)+population(k(2),:))/2+beta.*(population(k(1),:)-population(k(2),:))./2; %产生第一个子代
newpopulation(i*2,:)=(population(k(1),:)+population(k(2),:))/2-beta.*(population(k(1),:)-population(k(2),:))./2; %产生第二个子代
end
%% 变异
k=rand(size(newpopulation)); %随机选定要变异的基因位
miu=rand(size(newpopulation)); %采用多项式变异
temp=k<1/poplength & miu<0.5; %要变异的基因位
newpopulation(temp)=newpopulation(temp)+(maxvalue(temp)-minvalue(temp)).*((2.*miu(temp)+(1-2.*miu(temp)).*(1-(newpopulation(temp)-minvalue(temp))./(maxvalue(temp)-minvalue(temp))).^21).^(1/21)-1); %变异情况一
newpopulation(temp)=newpopulation(temp)+(maxvalue(temp)-minvalue(temp)).*(1-(2.*(1-miu(temp))+2.*(miu(temp)-0.5).*(1-(maxvalue(temp)-newpopulation(temp))./(maxvalue(temp)-minvalue(temp))).^21).^(1/21)); %变异情况二
%% 越界处理/种群合并
newpopulation(newpopulation>maxvalue)=maxvalue(newpopulation>maxvalue); %子代越上界处理
newpopulation(newpopulation<minvalue)=minvalue(newpopulation<minvalue); %子代越下界处理
newpopulation=[population;newpopulation]; %合并父子种群
%% 计算目标函数值
functionvalue=zeros(size(newpopulation,1),2); %合并后种群的各目标函数值,这里的问题是ZDT1
functionvalue(:,1)=newpopulation(:,1); %计算第一维目标函数值
g=1+9*sum(newpopulation(:,2:poplength),2)./(poplength-1);
functionvalue(:,2)=g.*(1-(newpopulation(:,1)./g).^0.5); %计算第二维目标函数值
%% 非支配排序,NSGA-II论文中的算法
Sp = zeros(size(newpopulation,1)); %Sp解p支配的解的集合
np = zeros(size(newpopulation,1),1); %支配解p的解的数量
Prank = zeros(size(newpopulation,1),1); %每个解的前沿面编号
F = zeros(size(newpopulation,1)); %保存每层前沿面的个体
for p = 1:size(newpopulation,1)
for q = 1:size(newpopulation,1)
if isDomin(functionvalue,p,q)
Sp(p,sum(Sp(p,:)~=0)+1) = q;
elseif isDomin(functionvalue,q,p)
np(p) = np(p)+1;
end
end
if np(p)==0
Prank(p) = 1;
F(1,sum(F(1,:)~=0)+1) = p;
end
end
i = 1;
while sum(F(i,:)~=0)
Q = zeros(1,size(F,2));
for p = 1:sum(F(i,:)~=0)
for q = 1:sum(Sp(F(i,p),:)~=0)
np(Sp(F(i,p),q)) = np(Sp(F(i,p),q)) - 1;
if np(Sp(F(i,p),q))==0
Prank(Sp(F(i,p),q)) = i+1;
Q(sum(Q(:)~=0)+1) = Sp(F(i,p),q);
end
end
end
i = i+1;
F(i,:) = Q;
end
%% 计算拥挤距离/选出下一代个体
fnum = 0;
psum = 0;
while psum <= popnum %判断前多少个面的个体能完全放入下一代种群
fnum = fnum + 1;
psum = psum + sum(F(fnum,:)~=0);
end
num = popnum - (psum - sum(F(fnum,:)~=0)); %num表示在当前前沿面需要多少个个体
population(1:popnum-num,:) = newpopulation(Prank<fnum,:);
% 计算当前前沿面个体的拥挤距离
I = F(fnum,:);
l = sum(I(:)~=0);
I = I(1:l);
I_distance = zeros(l,1);
fmax = max(functionvalue(I,:),[],1);
fmin = min(functionvalue(I,:),[],1);
for m = 1:size(functionvalue,2)
[~,oldsite] = sortrows(functionvalue(I,m));
I_distance(oldsite(1)) = inf;
I_distance(oldsite(end)) = inf;
for i = 2:l-1
I_distance(oldsite(i)) = I_distance(oldsite(i)) + (functionvalue(I(oldsite(i+1)),m)-functionvalue(I(oldsite(i-1)),m))/(fmax(m)-fmin(m));
end
end
I = sortrows([I_distance,I'],1,'descend'); %按拥挤距离降序排序
population(popnum-num+1:popnum,:) = newpopulation(I(1:num,2),:); %将第fnum个面上拥挤距离较大的前num个个体复制入下一代
end
%% 程序输出
fprintf('已完成,耗时%4s秒\n',num2str(toc)); %程序最终耗时
output=sortrows(functionvalue(Prank==1,:)); %最终结果:种群中非支配解的函数值
plot(output(:,1),output(:,2),'*b'); %作图
axis([0,1,0,1]);xlabel('F_1');ylabel('F_2');title('ZDT1')
结果
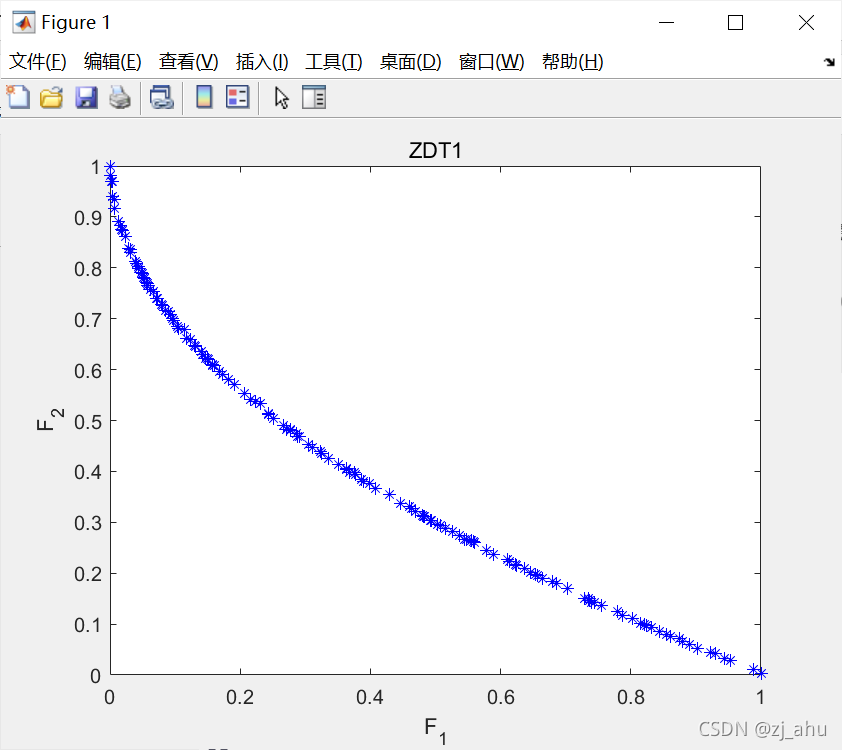
多目标优化经典算法——NSGA-II的更多相关文章
- 目标检测 | 经典算法 Cascade R-CNN: Delving into High Quality Object Detection
作者从detector的overfitting at training/quality mismatch at inference问题入手,提出了基于multi-stage的Cascade R-CNN ...
- 多目标优化算法(一)NSGA-Ⅱ(NSGA2)(转载)
多目标优化算法(一)NSGA-Ⅱ(NSGA2) 本文链接:https://blog.csdn.net/qq_40434430/article/details/82876572多目标优化算法(一)NSG ...
- 从NSGA到 NSGA II
NSGA(非支配排序遗传算法).NSGAII(带精英策略的非支配排序的遗传算法),都是基于遗传算法的多目标优化算法,都是基于pareto最优解讨论的多目标优化,遗传算法已经做过笔记,下面介绍paret ...
- 机器学习经典算法详解及Python实现--基于SMO的SVM分类器
原文:http://blog.csdn.net/suipingsp/article/details/41645779 支持向量机基本上是最好的有监督学习算法,因其英文名为support vector ...
- 脑洞大开--一条项目中常用的linux命令引发的经典算法题
小时候家里定了<读者>的月刊,里面记录一个故事:说有有个偏僻的乡村一日突然来了一个美女,她携着万贯家财子女在当地安家落户,成了当地的乡绅.她让她的子女世世代代的保守这个秘密,直到这个秘密不 ...
- 一条项目中常用的linux命令引发的经典算法题
小时候家里定了<读者>的月刊,里面记录一个故事:说有有个偏僻的乡村一日突然来了一个美女,她携着万贯家财子女在当地安家落户,成了当地的乡绅.她让她的子女世世代代的保守这个秘密,直到这个秘密不 ...
- AI佳作解读系列(二)——目标检测AI算法集杂谈:R-CNN,faster R-CNN,yolo,SSD,yoloV2,yoloV3
1 引言 深度学习目前已经应用到了各个领域,应用场景大体分为三类:物体识别,目标检测,自然语言处理.本文着重与分析目标检测领域的深度学习方法,对其中的经典模型框架进行深入分析. 目标检测可以理解为是物 ...
- Java中的经典算法之选择排序(SelectionSort)
Java中的经典算法之选择排序(SelectionSort) 神话丿小王子的博客主页 a) 原理:每一趟从待排序的记录中选出最小的元素,顺序放在已排好序的序列最后,直到全部记录排序完毕.也就是:每一趟 ...
- JS的十大经典算法排序
引子 有句话怎么说来着: 雷锋推倒雷峰塔,Java implements JavaScript. 当年,想凭借抱Java大腿火一把而不惜把自己名字给改了的JavaScript(原名LiveScript ...
- 三白话经典算法系列 Shell排序实现
山是包插入的精髓排序排序,这种方法,也被称为窄增量排序.因为DL.Shell至1959提出命名. 该方法的基本思想是:先将整个待排元素序列切割成若干个子序列(由相隔某个"增量"的元 ...
随机推荐
- C语言------结构体和共用体
仅供借鉴.仅供借鉴.仅供借鉴(整理了一下大一C语言每个章节的练习题.没得题目.只有程序了) 文章目录 1 .实训名称 2 .实训目的及要求 3.源代码及运行截图 4 .小结 1 .实训名称 实训8:结 ...
- (数据科学学习手札145)在Python中利用yarl轻松操作url
本文示例代码已上传至我的Github仓库https://github.com/CNFeffery/DataScienceStudyNotes 1 简介 大家好我是费老师,在诸如网络爬虫.web应用开发 ...
- Springboot 一行代码实现文件上传 20个平台!少写代码到极致
大家好,我是小富~ 技术交流,公众号:程序员小富 又是做好人好事的一天,有个小可爱私下问我有没有好用的springboot文件上传工具,这不巧了嘛,正好我私藏了一个好东西,顺便给小伙伴们也分享一下,d ...
- 【题解】CF991C Candies
题面传送门 解决思路 看到 \(10^{18}\) 的范围,我们可以想到二分答案.只要对于每一个二分出的答案进行 \(check\) ,如果可行就往比它小的半边找,不可行就往比它大的半边找. 以下是 ...
- Vue3笔记(二)了解组合式API的应用与方法
一.组合式API(Composition API)的介绍 官方文档: https://v3.cn.vuejs.org/guide/composition-api-introduction.html 组 ...
- PLC攻击(一):应用层攻击
转载请注明出处:信安科研人please subscribe my official wechat :信安科研人获取更多安全资讯 参考文献: A Stealth Program Injection ...
- Bugku login1
打开是个普普通通的登录界面,盲猜是注入题,先看看源码吧,没找到什么有用的信息,那就先注册试试 注册admin就已经存在,可能待会就爆破admin的密码也可能,因为没有验证嘛 试试注册其他的 登录发现他 ...
- 痞子衡嵌入式:MCUXpresso IDE下高度灵活的FreeMarker链接文件模板机制
大家好,我是痞子衡,是正经搞技术的痞子.今天痞子衡给大家分享的是MCUXpresso IDE下高度灵活的FreeMarker链接文件模板机制. 痞子衡之前写过一篇文章 <MCUXpresso I ...
- c++学习笔记(入门)
1 struct和class的区别 struct成员变量(成员函数)的访问属性缺省的情况下默认为public. class成员变量(成员函数)的访问属性缺省的情况下默认为private. 2 初始化列 ...
- KVC原理与数据筛选
作者:宋宏帅 1 前言 在技术论坛中看到一则很有意思的KVC案例: @interface Person : NSObject @property (nonatomic, copy) NSString ...
