掌控(control) 方法记录

掌控(control)

题面描述

公元\(2044\)年，人类进入了宇宙纪元。L国有\(n\)个星球，分别编号为\(1\)到\(n\)，每一星球上有一个球长。有些球长十分强大，可以管理或掌控其他星球的球长，具体来说，第\(i\)个星球的球长管理\(k_i+1\)个星球的球长，分别是 \(a_{i1},a_{i2},...,a_{iki}(a_{ij}<i)\)，但若想要掌控一个星球的球长，就没那么容易了，第\(i\)个星球的球长掌控第\(j\)个星球的球长当且仅当他管理的所有球长都掌控第\(j\)个星球的球长，当然，所有球长都掌控他自己。

这些球长要召开\(q\)次会议，每次会议由\(t_i\)个球长召开，所有被他们掌控的球长都会参加，你作为宇宙会议室室长，需要知道每次会议有多少个球长参加。

输入

第一行一个数\(n\)，表示星球的个数；

接下来\(n\)行，每一行首先给出一个\(k_i\)（可能为\(0\)），接下来\(k_i\)个数，描述第\(i\)个星球的球长管理的球长。保证没有重复；

接下来一行，给出一个数\(q\)，表示询问的个数；

接下来\(q\)行，每一行描述一个询问：格式同上文的格式。不保证没有重复（重复的球长当做只出现了一次）

输出

输出共\(q\)行，第\(i\)行输出第\(i\)次询问的答案。

样例输入

7
0
1 1
1 1
1 2
2 2 3
0
2 2 6
3
2 2 3
2 3 5
2 4 5

样例输出

3
3
4

样例解释

对于第一个询问，2、3号球长都掌控1号球长，所以总共有3个球长参会，编号分别为1，2，3；

对于第二个询问，3、5号球长都掌控1号球长，所以总共有3个球长参会，编号分别为1，3，5；

对于第三个询问，4号球长掌控第1、2号球长，所以总共有4个球长参会，编号分别为1，2，4，5；

特别说明：第5号球长没有掌控球长2，因为3属于\(k_5\),但2不属于\(k_3\)。但球长4掌控球长2，因为球长掌控自己。

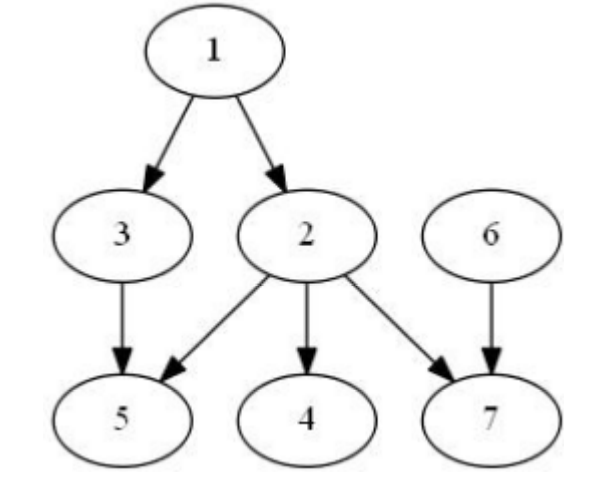
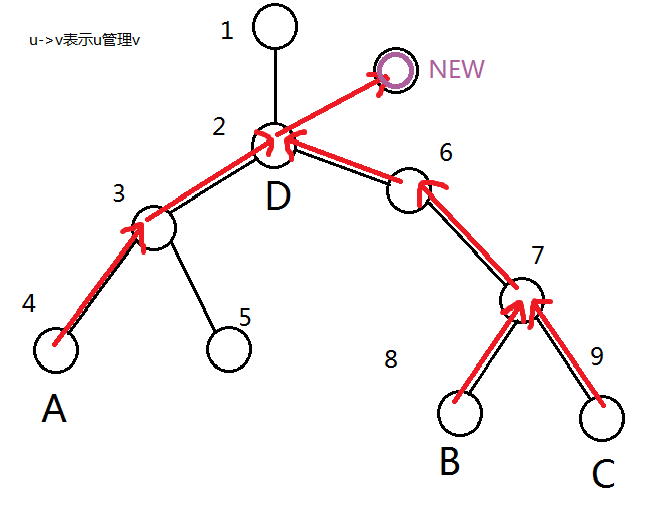
图片说明：u->v表示v管理u

数据范围

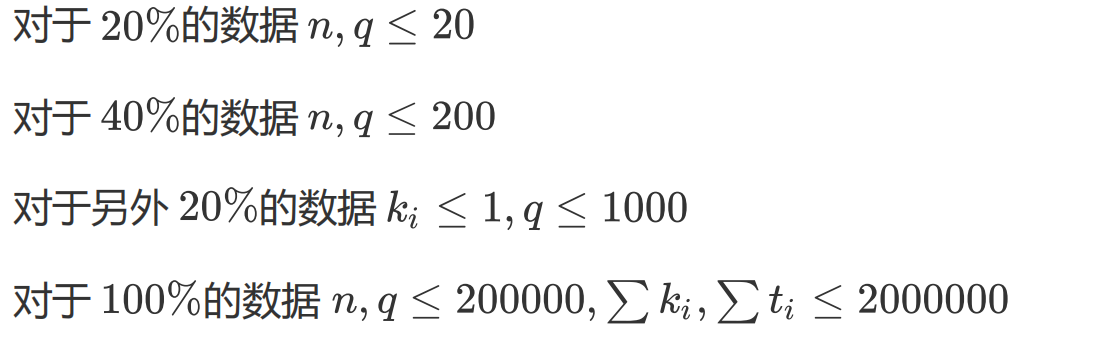
题解

暴力做法（40pts）

仔细阅读数据范围，发现部分分的\(n,q\)较小，为了方便处理，我们可以用类似邻接矩阵的思路来存。

考虑所有可能需要储存的信息，我们开以下数组。

bool vis[N];//i是否与会
int con1[N][N];//i管理j
int cnt1[N];//i管理的球长数量
int con2[N][N];//i掌控j
int cnt2[N];//i掌控的球长数量
int ans1[N][N];//i的第j个管理的球长为n
int ans2[N][N];//i的第j个掌控的球长为n

然后依照题意进行模拟，求出每一个球长的掌控情况，最后求出与会者掌控情况的并集即可。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=2005;
int n,q;
int final;
int meet;//开会
bool vis[N];//i是否与会
int con1[N][N];//i管理j
int cnt1[N];//i管理的球长数量
int con2[N][N];//i掌控j
int cnt2[N];//i掌控的球长数量
int ans1[N][N];//i的第j个管理的球长为n
int ans2[N][N];//i的第j个掌控的球长为n
int main()
{
	freopen("control.in","r",stdin);
	freopen("control.out","w",stdout);
	scanf("%d",&n);
	for(int i=1,k;i<=n;i++)
	{
		scanf("%d",&k);
		cnt1[i]=k;
		for(int j=1,m;j<=k;j++)
		{
			scanf("%d",&m);
			con1[i][m]=1;
			ans1[i][j]=m;
		}
	}

	for(int i=1;i<=n;i++)
	{
		ans2[i][1]=i;
		con2[i][i]=1;
		cnt2[i]=1;
	}

	for(int i=1;i<=n;i++)
	{
		if(!cnt1[i]) continue;
		for(int j=1;j<=n;j++)//i是否掌控j
		{
			bool flag=0;
			for(int l=1;l<=cnt1[i];l++)
			{
				int nxt=ans1[i][l];//nxt是i管理的第l个球长
				if(!con2[nxt][j])
				{
					flag=1;//nxt无法掌控j
					break;
				}
			}
			if(!flag)
			{
				con2[i][j]=1;
				cnt2[i]++;
				ans2[i][cnt2[i]]=j;
			}
		}
	}

	scanf("%d",&q);
	for(int i=1,t;i<=q;i++)
	{
		final=0;
		scanf("%d",&t);
		memset(vis,0,sizeof(vis));
		meet=0;
		for(int j=1;j<=t;j++)
		{
			scanf("%d",&meet);
			for(int l=1;l<=cnt2[meet];l++)
			{
				vis[ans2[meet][l]]=1;
			}
		}
		for(int j=1;j<=n;j++)
		{
			if(vis[j]) final++;
		}
		printf("%d\n",final);
	}
	return 0;
}

正解

暴力为什么会寄？首先是存状态的方式不科学：消耗空间过大，且维护起来相当笨重。其次是维护的效率低下：纯模拟，导致很多不必要的重复运算。

怎么解决呢？首先来看更好的存状态方式。

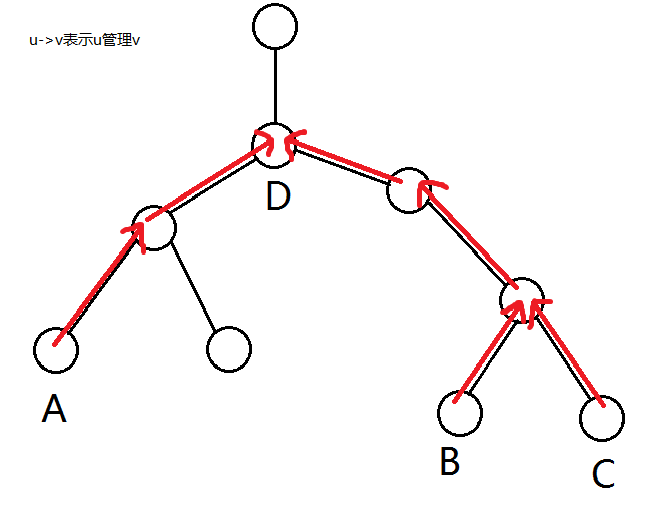
如图，倘若想要掌控\(A,B,C\)，那么我们只需要掌控它们的最近公共祖先\(D\)即可，即所有点的掌控关系是一棵树，新进的节点就应该接到它掌控的所有节点的LCA,即上文的\(D\)。而我们自然而然就选择树形结构来存。

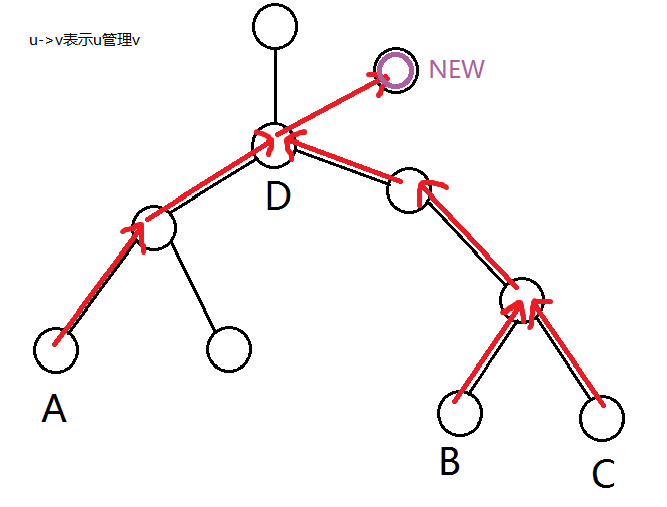
为了提高效率，我们选择边建树边倍增，建树复杂度\(nlogn\)。

void cone(int a,int b)//cone=conect
{
	f[a][0]=b;
	dep[a]=dep[b]+1;
	add(b,a);
	for(int i=1;f[f[a][i-1]][i-1];i++)
	{
		f[a][i]=f[f[a][i-1]][i-1];
	}
}
int get_lca(int x,int y)//倍增lca
{
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=19;i>=0;i--)
		if(dep[f[x][i]]>=dep[y])
			x=f[x][i];
	if(x==y) return x;
	for(int i=19;i>=0;i--)
		if(f[x][i]!=f[y][i])
			x=f[x][i],y=f[y][i];
	return f[x][0];
}

再考虑回答询问。

根据我们建树时遵循的求LCA的原则，发现每个询问就是求给出所有点到根的并集的节点数。考虑将所有节点按\(dfn\)排序，则将每个节点与其相邻的节点的LCA加起来就是答案。

void dfs(int now)//求dfn
{
	dfn[now]=++cnt;
	for(int i=head[now];i;i=E[i].nex) dfs(E[i].v);
}

for(int i=1,t;i<=q;i++)
	{
		re(t);
		for(int j=1;j<=t;j++) re(meet[j]);
		sort(meet+1,meet+t+1,cmp);//按dfn排序
		int ans=dep[meet[1]];
		for(int j=2;j<=t;j++) ans+=dep[meet[j]]-dep[get_lca(meet[j],meet[j-1])];
		printf("%d\n",ans);
	}

完整AC代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=200005;
template <typename T>inline void re(T &x) {
	x=0;
	int f=1;
	char c=getchar();
	for(;!isdigit(c);c=getchar()) if(c=='-') f=-f;
	for(;isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^48);
	x*=f;
	return;
}
int n,q;
int head[N],totr;
struct edge
{
	int u,v,nex;
}E[N<<1];
void add(int u,int v)
{
	E[totr++].u=u;
	E[totr].v=v;
	E[totr].nex=head[u];
	head[u]=totr;
}
int f[N][20],dfn[N],meet[N],dep[N];
void cone(int a,int b)//cone=conect
{
	f[a][0]=b;
	dep[a]=dep[b]+1;
	add(b,a);
	for(int i=1;f[f[a][i-1]][i-1];i++)
	{
		f[a][i]=f[f[a][i-1]][i-1];
	}
}
int get_lca(int x,int y)//倍增lca
{
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=19;i>=0;i--)
		if(dep[f[x][i]]>=dep[y])
			x=f[x][i];
	if(x==y) return x;
	for(int i=19;i>=0;i--)
		if(f[x][i]!=f[y][i])
			x=f[x][i],y=f[y][i];
	return f[x][0];
}
int cnt;
void dfs(int now)//求dfn
{
	dfn[now]=++cnt;
	for(int i=head[now];i;i=E[i].nex) dfs(E[i].v);
}
bool cmp(int a,int b)
{
	return dfn[a]<dfn[b];
}
int main()
{
	freopen("control.in","r",stdin);
	freopen("control.out","w",stdout);
	re(n);
	for(int i=1,k;i<=n;i++)
	{
		re(k);
		int lca=0;
		if(k) re(lca);
		for(int j=1,mana;j<k;j++)
		{
			re(mana);
			lca=get_lca(lca,mana);
		}
		cone(i,lca);
	}
	re(q);
	dfs(0);
	for(int i=1,t;i<=q;i++)
	{
		re(t);
		for(int j=1;j<=t;j++) re(meet[j]);
		sort(meet+1,meet+t+1,cmp);//按dfn排序
		int ans=dep[meet[1]];
		for(int j=2;j<=t;j++) ans+=dep[meet[j]]-dep[get_lca(meet[j],meet[j-1])];
		printf("%d\n",ans);
	}
	return 0;
}

参考