树链剖分+线段树 CF 593D Happy Tree Party（快乐树聚会）

题目链接

题意：

　　有n个点的一棵树，两种操作：

　　1. a到b的路径上，给一个y，对于路径上每一条边，进行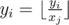操作，问最后的y；

　　2. 修改某个条边p的值为c

思路：

　　链上操作的问题，想树链剖分和LCT，对于第一种操作，因为是向下取整，考虑y除以路径上所有边乘积，即；对于第二种操作，就是线段树上的单点更新。因为给的是边的序号，首先每个id能知道对应的边值（ide[]）和连接的点（idv[]）。还有乘法溢出的处理，写成函数方便多了。

另外：

　　1. 用dfn来替换dep完全没有问题，那以后就用dfn吧。2. 第二次DFS，要先去重儿子的路，这样dfn[son[u]]=dfn[u]+1，son数组也省了。3. 代码debug水平有待提升。4. 树的建图用vector就行了，不需要邻接表（n-1条边）。

#include <bits/stdc++.h>

typedef long long ll;
const int N = 2e5 + 5;
const ll INF = 2e18;

std::vector<std::pair<int, int> > edges[N];
int n, m;

int dfn[N], fa[N], son[N], sz[N], belong[N];
ll ide[N];
int idv[N];
int tim;

inline ll mul(ll a, ll b) {
    if (a != 0 && b > INF / a) return INF;
    return a * b;
}

void DFS2(int u, int chain) {
    dfn[u] = ++tim;
    belong[u] = chain;
    if (son[u] != 0) {
        DFS2 (son[u], chain);
    }
    for (auto e: edges[u]) {
        int v = e.first;
        if (v == fa[u] || v == son[u]) continue;
        DFS2 (v, v);
    }
}

void DFS1(int u, int pa) {
    sz[u] = 1;
    fa[u] = pa;
    for (auto e: edges[u]) {
        int v = e.first, id = e.second;
        if (v == pa) continue;
        idv[id] = v;
        DFS1 (v, u);
        if (sz[v] > sz[son[u]]) son[u] = v;
        sz[u] += sz[v];
    }
}

#define lson l, mid, o << 1
#define rson mid + 1, r, o << 1 | 1

ll val[N<<2];

void push_up(int o) {
    val[o] = mul (val[o<<1], val[o<<1|1]);
}

void tree_updata(int p, ll c, int l, int r, int o) {
    if (l == r) {
        val[o] = c;
        return ;
    }
    int mid = l + r >> 1;
    if (p <= mid) tree_updata (p, c, lson);
    else tree_updata (p, c, rson);
    push_up (o);
}

ll tree_query(int ql, int qr, int l, int r, int o) {
    if (ql <= l && r <= qr) {
        return val[o];
    }
    int mid = l + r >> 1;
    ll ret = 1;
    if (ql <= mid) ret = mul (ret, tree_query (ql, qr, lson));
    if (qr > mid) ret = mul (ret, tree_query (ql, qr, rson));
    return ret;
}

ll query(int a, int b) {
    ll ret = 1;
    int p = belong[a], q = belong[b];
    while (p != q) {
        if (dfn[p] < dfn[q]) {
            std::swap (p, q);
            std::swap (a, b);
        }
        ret = mul (ret, tree_query (dfn[p], dfn[a], 1, n, 1));
        a = fa[p];
        p = belong[a];
    }
    if (dfn[a] < dfn[b]) std::swap (a, b);
    if (a != b) {
        ret = mul (ret, tree_query (dfn[son[b]], dfn[a], 1, n, 1));
    }
    return ret;
}

void modify(int id, ll c) {
    tree_updata (dfn[idv[id]], c, 1, n, 1);
}

void prepare() {
    DFS1 (1, 0);
    tim = 0;
    DFS2 (1, 1);
    for (int i=1; i<n; ++i) {
        tree_updata (dfn[idv[i]], ide[i], 1, n, 1);
    }
}

int main() {
    scanf ("%d%d", &n, &m);
    for (int i=1; i<n; ++i) {
        int u, v;
        ll w;
        scanf ("%d%d%I64d", &u, &v, &w);
        ide[i] = w;
        edges[u].push_back ({v, i});
        edges[v].push_back ({u, i});
    }

    prepare ();

    for (int i=0; i<m; ++i) {
        int t, a, b;
        ll c;
        scanf ("%d%d", &t, &a);
        if (t == 1) {
            scanf ("%d%I64d", &b, &c);
            printf ("%I64d\n", c / query (a, b));
        } else {
            scanf ("%I64d", &c);
            modify (a, c);
        }
    }
    return 0;
}