python中functools.singledispatch的使用

from functools import singledispatch

@singledispatch
def show(obj):
    print (obj, type(obj), "obj")

@show.register(str)
def _(text):
    print (text, type(text), "str")

@show.register(int)
def _(n):
    print (n, type(n), "int")
show(1)
show("xx")
show([1])

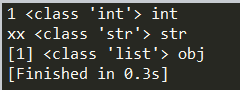
为show函数传递不同的类型参数，就表现不同的行为