组合数学入门—TwelveFold Way

组合数学入门—TwelveFold Way

你需要解决\(12\)个组合计数问题。

\(n\)个有标号/无标号的球分给\(m\)个有标号/无标号的盒子

盒子有三种限制：

A、无限制

B、每个盒子至少有一个球

C、每个盒子至多有一个球

共有\(2\times2\times3=12\)种问题：

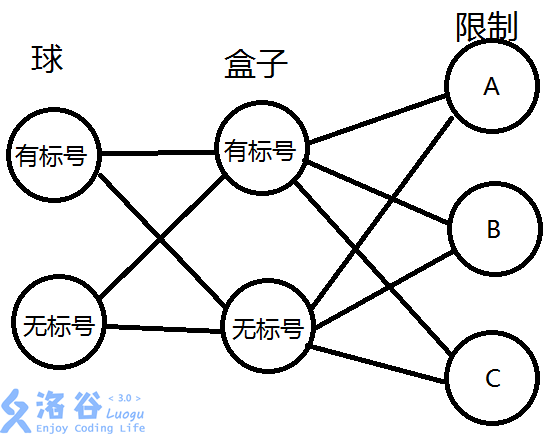
为了方便 将有标号记为L(labelled) 无标号记为U(unlabelled)

那么一个问题可以用缩写代替，如ULA表示\(n\)个无标号的球分给\(m\)个有标号的盒子，一共有多少种方案。

现在你的任务是，给定问题的缩写和\(n,m\)，求方案数对\(998244353\)取模后的值。

LLA

这个很明显答案是\(m^n\),每一个球有\(m\)种选择

LLB

发现这个条件不好满足,考虑容斥,每次强制枚举\(i\)个盒子里面没有球
\[
ans = \sum_{i = 0}^m\binom{n}{i}(m - i)^n
\]

LLC

我们发现,因为要求球全部放入盒子,所以当\(n > m\)肯定无解

否则答案就是
\[
\binom{m}{n}\times n!
\]
看看那几个盒子里面有球,并且因为球是不同的,所以要再乘上排列数

LUB

发现LUB和LLB的区别就是其实就是\(\{1,2,3\},\{4,5\}\)和\(\{4,5\}\),\(\{1,2,3\}\)看做一种

那么我们直接把LLB的答案除以\(m!\)即可

这就引出了我们要介绍的东西,第二类斯特林数

第二类斯特林数,记为\(S\),\(S_n^m\)表示把\(n\)个有标号的球放到\(m\)个无标号的盒子里面的方案数

我们可以比较简单的理解第二类斯特林数的递推公式
\[
S_{n}^m = S_{n - 1}^{m - 1}+ m\times S_{n - 1}^m
\]
每次新开一个盒子放\(i\)或者是放入之前的任何一个集合之中

LUA

我们既然知道了LLB的答案,直接枚举多少个盒子放了球
\[
ans = \sum_{i = 1}^mS_{n}^i
\]
到此为止我们可以发现一个奇妙的性质A和B是知一推一的,有无标号仅仅通过乘组合数推出来

LUC

这就是比较水的了,直接判断能否放下,放得下就是\(1\)

ULB

经典插板法的模型,ULB也可以在做是这样一个方程的正整数解的个数
\[
x_1+x_2+x_3+\dots +x_m = n
\]
那么我们看做这样\(n\)的球插入\(m - 1\)的版子.分割成\(m\)部分的方案数

所以方案数就是
\[
\binom{n - 1}{m - 1}
\]

ULA

我们继续上面的方程

设\(y_i = x_i+ 1\)

也就是我们现在要解决这个方程的正整数解的个数
\[
y_1+y_2+\dots+y_m = n+m
\]
同理,可以知道是
\[
\binom{n + m - 1}{m - 1}
\]
每一组\(y\)都对应着唯一一组\(x\)(因为\(x\)和\(y\)的关系是确定的)

ULC

首先,\(n > m\)肯定无解,接下来只需要考虑\(n\le m\)

否则答案就是\(\binom{m}{n}\)

UUC

同LUC

UUB

这个不能通过ULB除以\(m!\)得到

因为ULB中我们尽管盒子不同,但是球是相同的,所以我们会把\(\{2,3,3\}\)和\(\{2,3,3\}\)看做同一种方案,所以直接除以\(m!\)的前提是上面的例子被看做不同方案,否则就没有排列一说

那我们设\(P_{i,j}\)表示\(i\)个无标号的球分到\(j\)个有标号的盒子里的方案数

为了保证不会重复计数,我们强制盒子的球数目不增

转移要么把新球新开一个盒子,要么在前面所有盒子都放一个球
\[
P_{i.j} = P_{i - 1,j - 1} + P_{i - j,j}
\]
转移边界有\(P_{0,0} = 1\)

这其实就是划分数

UUA

首先,我们可以采用老套路,暴力枚举有多少个盒子中放球
\[
ans = \sum_{i = 1}^m P_n^i
\]
另外类似于ULA的思路,我们发现答案其实是\(P_{n + m}^m\)