沈阳网络赛 F - 上下界网络流

"Oh, There is a bipartite graph.""Make it Fantastic."

X wants to check whether a bipartite graph is a fantastic graph. He has two fantastic numbers, and he wants to let all the degrees to between the two boundaries. You can pick up several edges from the current graph and try to make the degrees of every point to between the two boundaries. If you pick one edge, the degrees of two end points will both increase by one. Can you help X to check whether it is possible to fix the graph?

Input

There are at most 303030 test cases.

For each test case,The first line contains three integers NNN the number of left part graph vertices, MMM the number of right part graph vertices, and KKK the number of edges ( 1≤N≤20001 \le N \le 20001≤N≤2000,0≤M≤20000 \le M \le 20000≤M≤2000,0≤K≤60000 \le K \le 60000≤K≤6000 ). Vertices are numbered from 111 to NNN.

The second line contains two numbers L,RL, RL,R (0≤L≤R≤300)(0 \le L \le R \le 300)(0≤L≤R≤300). The two fantastic numbers.

Then KKK lines follows, each line containing two numbers UUU, VVV (1≤U≤N,1≤V≤M)(1 \le U \le N,1 \le V \le M)(1≤U≤N,1≤V≤M). It shows that there is a directed edge from UUU-th spot to VVV-th spot.

Note. There may be multiple edges between two vertices.

Output

One line containing a sentence. Begin with the case number. If it is possible to pick some edges to make the graph fantastic, output "Yes" (without quote), else output "No" (without quote).

样例输入

3 3 7
2 3
1 2
2 3
1 3
3 2
3 3
2 1
2 1
3 3 7
3 4
1 2
2 3
1 3
3 2
3 3
2 1
2 1

样例输出

Case 1: Yes
Case 2: No

题目来源

ACM-ICPC 2018 沈阳赛区网络预赛

题意 ： 给你左右两侧分别给出 n 个点和 m 个点， 再给你其中的一些边，可以选择其中的任意个边，每次选择会使左右两边的点都增加 1， 要求所有点的范围都在 l ~ r 内， 问是否可行

思路分析 ：

　　打网络赛的时候，我们团队竟没有人想到网络流，多裸的一个题啊，当时就感觉这个可以用二分图去解决，，， 可惜当时并没有学过网络流，，，，

　　其实呢就是一个上下界网络流的水题，构建的图如下

　　

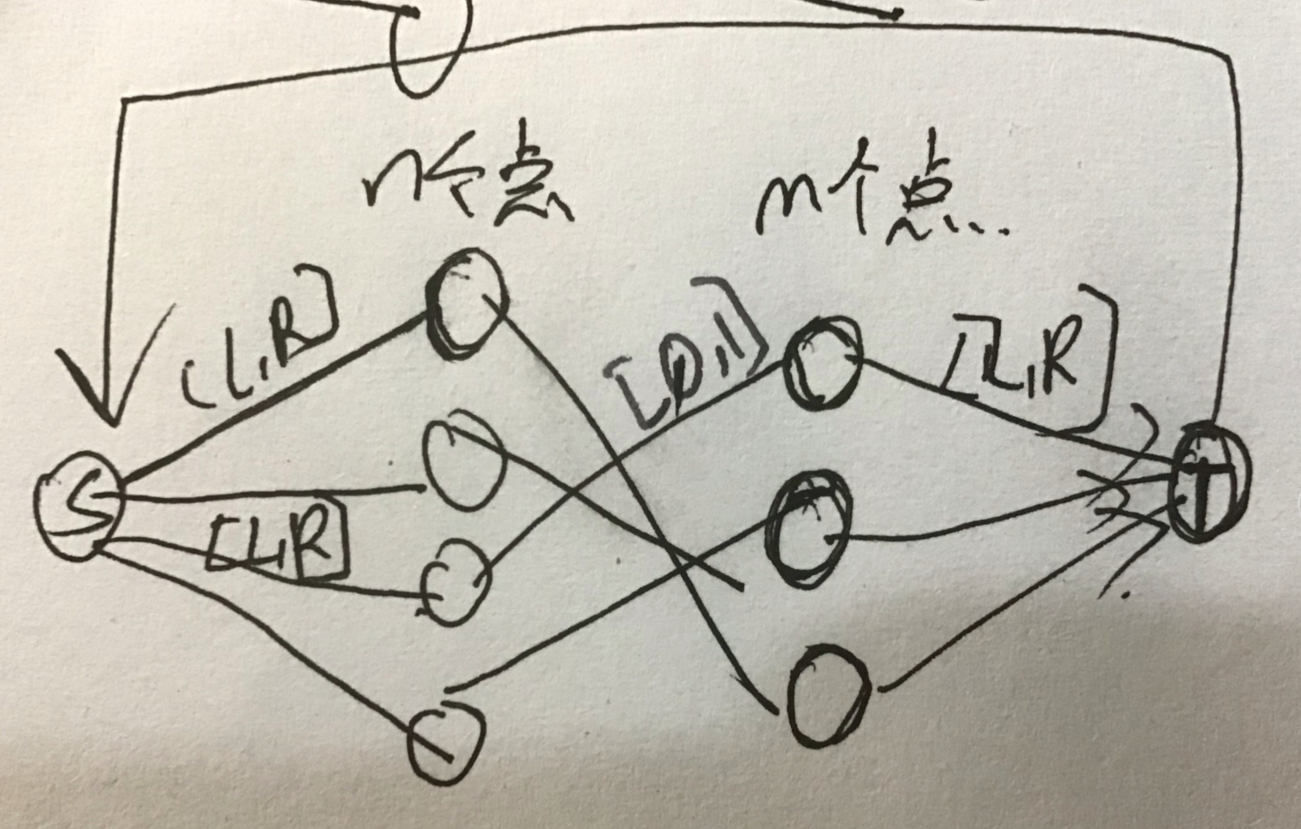
代码示例 ：

using namespace std;
#define ll long long
const int maxn = 1e5+5;
const int inf = 0x3f3f3f3f;

int n, m, k;
int l, r;
int sum = 0;
struct node
{
    int to, next, flow;
}e[maxn];
int head[maxn];
int cnt;

void init(){
    cnt = 0; sum = 0;
    memset(head, -1, sizeof(head));
}
void addedge(int u, int v, int w){
    e[cnt].to = v, e[cnt].flow = w, e[cnt].next = head[u], head[u] = cnt++;
    e[cnt].to = u, e[cnt].flow = 0, e[cnt].next = head[v], head[v] = cnt++;
}

int dep[maxn], que[maxn];
bool bfs(int s, int t){
    memset(dep, 0, sizeof(dep));
    dep[s] = 1, que[0] = s;
    int head1 = 0, tail = 1;
    while(head1 < tail) {
        int v = que[head1++];
        for(int i = head[v]; i != -1; i = e[i].next){
            int to = e[i].to;
            if (e[i].flow && !dep[to]){
                dep[to] = dep[v]+1;
                que[tail++] = to;
            }
        }
    }
    return dep[t];
}
int aim;
int dfs(int u, int f1){
    if (u == aim || f1 == 0) return f1;

    int f = 0;
    for(int i = head[u]; i != -1; i = e[i].next){
        int to = e[i].to;
        if (e[i].flow && dep[to] == dep[u]+1){
            int x = dfs(to, min(e[i].flow, f1));
            e[i].flow -= x, e[i^1].flow += x;
            f1 -= x, f += x;
            if (f1 == 0) return f;
        }
    }
    if (!f) dep[u] = -2;
    return f;
}
int kas = 1;

void maxflow(int s, int t){
    int res = 0; aim = t;

    while(bfs(s, t)){
        res += dfs(s, inf);
    }
    if (res == sum) printf("Case %d: Yes\n", kas++);
    else printf("Case %d: No\n", kas++);
}

int main() {
    int u, v;

    while(~scanf("%d%d%d", &n, &m, &k)){
        int s = 0, t = n+m+1;
        int ss = t+m+2, tt = n+m+3;
        init();
        scanf("%d%d", &l, &r);
        addedge(t, s, inf);
        for(int i = 1; i <= k; i++){
            scanf("%d%d", &u, &v);
            addedge(u, n+v, 1);
            addedge(u, tt, 0);
            addedge(ss, n+v, 0);
        }
        for(int i = 1; i <= n; i++){
            addedge(s, i, r-l);
            addedge(s, tt, l);
            addedge(ss, i, l);
        }
        for(int i = 1; i <= m; i++){
            addedge(n+i, t, r-l);
            addedge(n+i, tt, l);
            addedge(ss, t, l);
        }
        sum = l*(m+n);
        maxflow(ss, tt);
    }
    return 0;
}