机器学习理论基础学习3.1--- Linear classification 线性分类之感知机PLA（Percetron Learning Algorithm）

一、感知机（Perception）

1.1 原理：

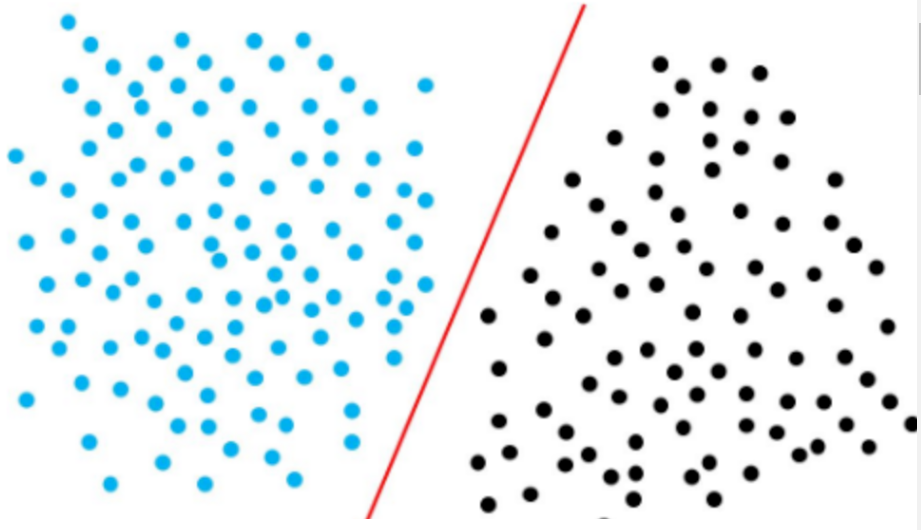
感知机是二分类的线性模型，其输入是实例的特征向量，输出的是事例的类别，分别是+1和-1，属于判别模型。

假设训练数据集是线性可分的，感知机学习的目标是求得一个能够将训练数据集正实例点和负实例点完全正确分开的分离超平面。如果是非线性可分的数据，则最后无法获得超平面。

1.2 感知机模型

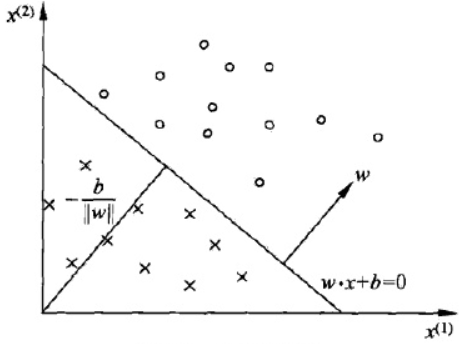
感知机从输入空间到输出空间的模型如下：

　　　　　　　　　　　　　　　　　　

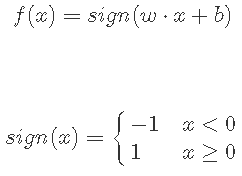
1.3 求解

思想：错误驱动

损失函数：期望使错误分类的所有样本，到超平面的距离之和最小

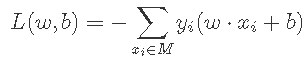　　（其中M集合是误分类点的集合）

学习算法：SGD（随机梯度下降）

　　感知机学习算法是对上述损失函数进行极小化，求得w和b。但是用普通的基于所有样本的梯度和的均值的批量梯度下降法（BGD）是行不通的，原因在于我们的损失函数里面有限定，只有误分类的M集合里面的样本才能参与损失函数的优化。所以我们不能用最普通的批量梯度下降,只能采用随机梯度下降（SGD）。目标函数如下：

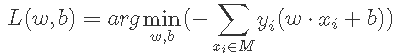
原始形式算法：

1.4 训练过程

线性可分的过程	线性不可分的过程

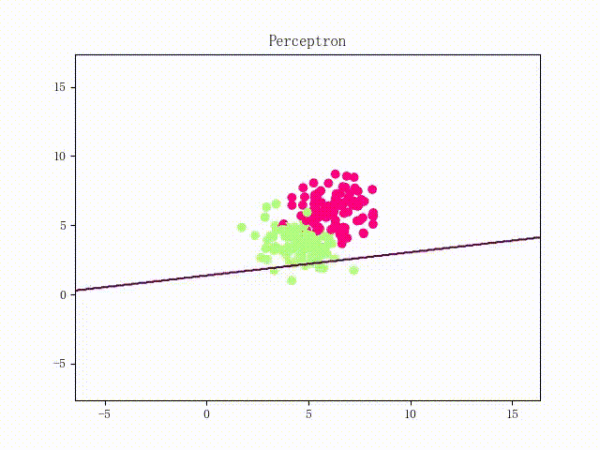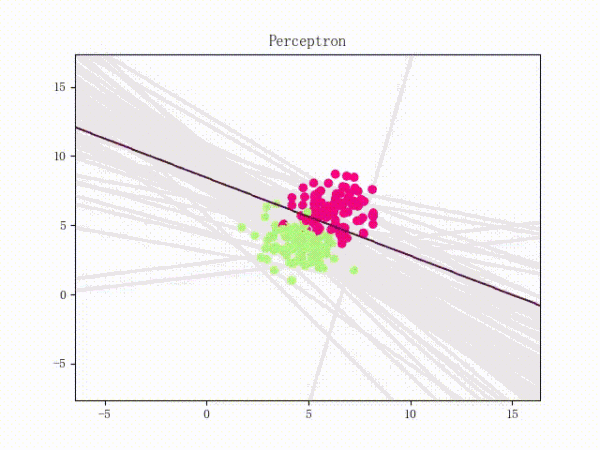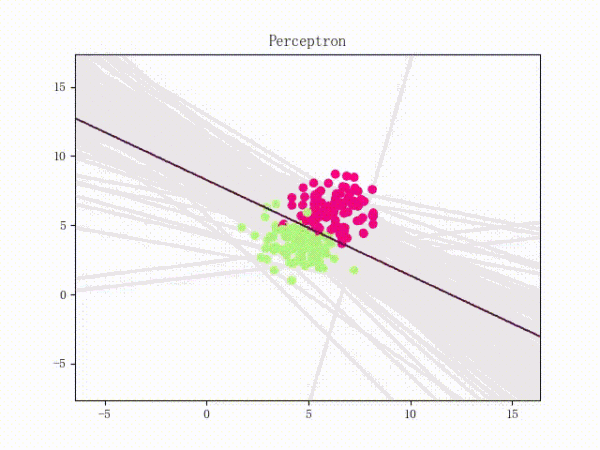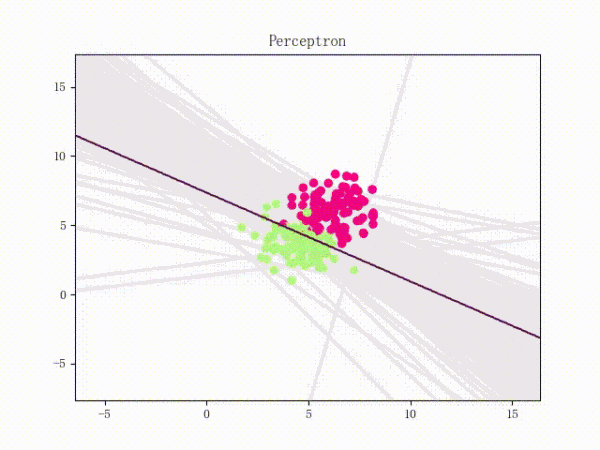1.5 小结

感知机算法是一个简单易懂的算法，它是很多算法的鼻祖，比如支持向量机算法，神经网络与深度学习。因此虽然它现在已经不是一个在实践中广泛运用的算法，还是值得好好的去研究一下。感知机算法对偶形式为什么在实际运用中比原始形式快，也值得好好去体会。

参考文献

1. 感知机原理（Perceptron）