【机器学习】主成分分析PCA（Principal components analysis）

1. 问题

真实的训练数据总是存在各种各样的问题：
　　1、 比如拿到一个汽车的样本，里面既有以“千米/每小时”度量的最大速度特征，也有“英里/小时”的最大速度特征，显然这两个特征有一个多余。
　　2、 拿到一个数学系的本科生期末考试成绩单，里面有三列，一列是对数学的兴趣程度，一列是复习时间，还有一列是考试成绩。我们知道要学好数学，需要有浓厚的兴趣，所以第二项与第一项强相关，第三项和第二项也是强相关。那是不是可以合并第一项和第二项呢？
　　3、 拿到一个样本，特征非常多，而样例特别少，这样用回归去直接拟合非常困难，容易过度拟合。比如北京的房价：假设房子的特征是（大小、位置、朝向、是否学区房、建造
年代、是否二手、层数、所在层数），搞了这么多特征，结果只有不到十个房子的样例。要拟合房子特征‐>房价的这么多特征，就会造成过度拟合。
　　4、 这个与第二个有点类似，假设在 IR 中我们建立的文档‐词项矩阵中，有两个词项为“learn”和“study”，在传统的向量空间模型中，认为两者独立。然而从语义的角度来讲，两者是相似的，而且两者出现频率也类似，是不是可以合成为一个特征呢？
　　5、 在信号传输过程中，由于信道不是理想的，信道另一端收到的信号会有噪音扰动，那么怎么滤去这些噪音呢？
　　回顾我们之前介绍的《模型选择和规则化》，里面谈到的特征选择的问题。但在那篇中要剔除的特征主要是和类标签无关的特征。比如“学生的名字”就和他的“成绩”无关，使用的是互信息的方法。
　　而这里的特征很多是和类标签有关的，但里面存在噪声或者冗余。在这种情况下，需要一种特征降维的方法来减少特征数，减少噪音和冗余，减少过度拟合的可能性。
下面探讨一种称作主成分分析（PCA）的方法来解决部分上述问题。 PCA 的思想是将 n维特征映射到 k 维上（k<n），这 k 维是全新的正交特征。这 k 维特征称为主元，是重新构造出来的 k 维特征，而不是简单地从 n 维特征中去除其余 n‐k 维特征。

2. PCA 计算过程

　　整个 PCA 过程貌似及其简单，就是求协方差的特征值和特征向量，然后做数据转换。

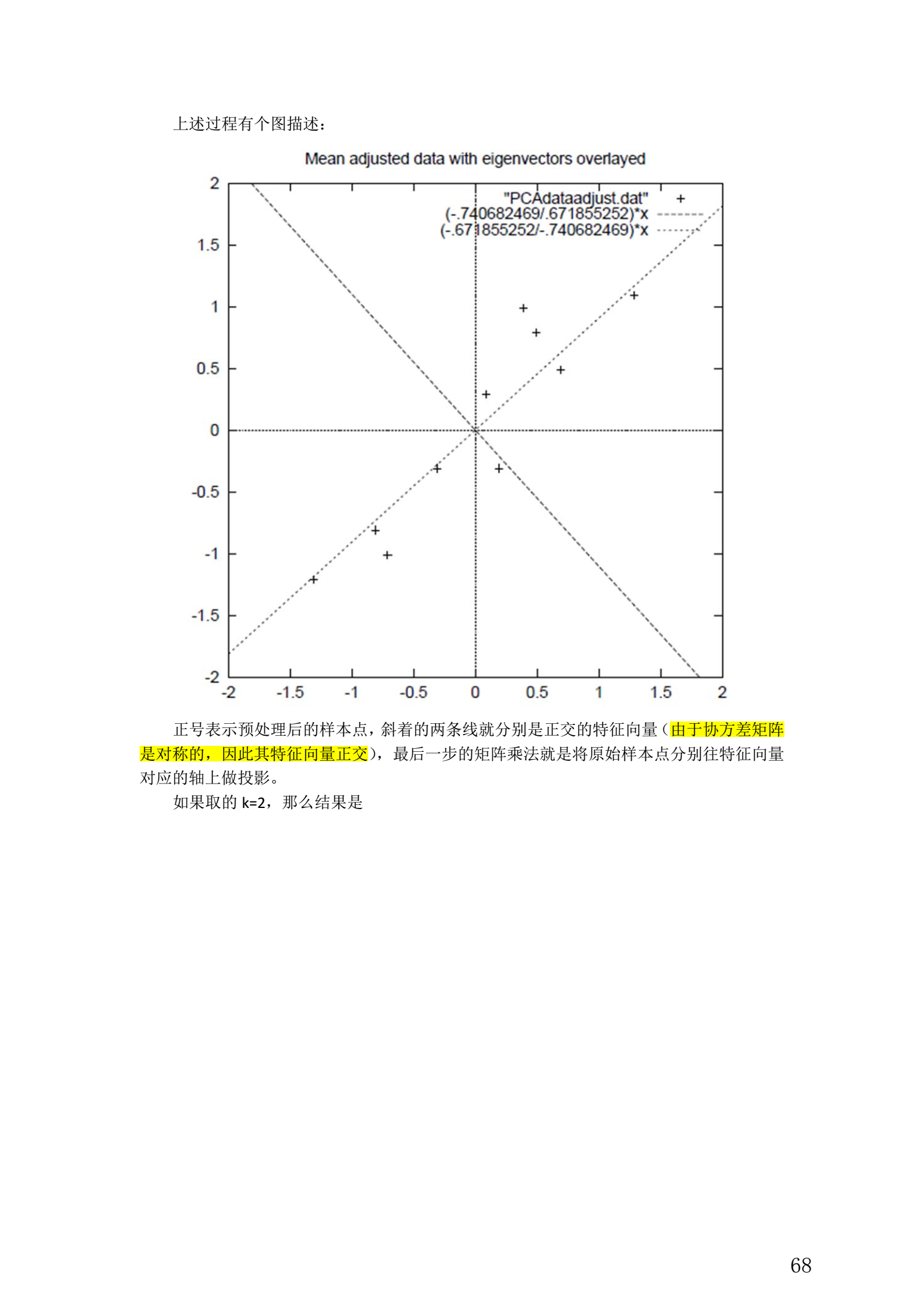
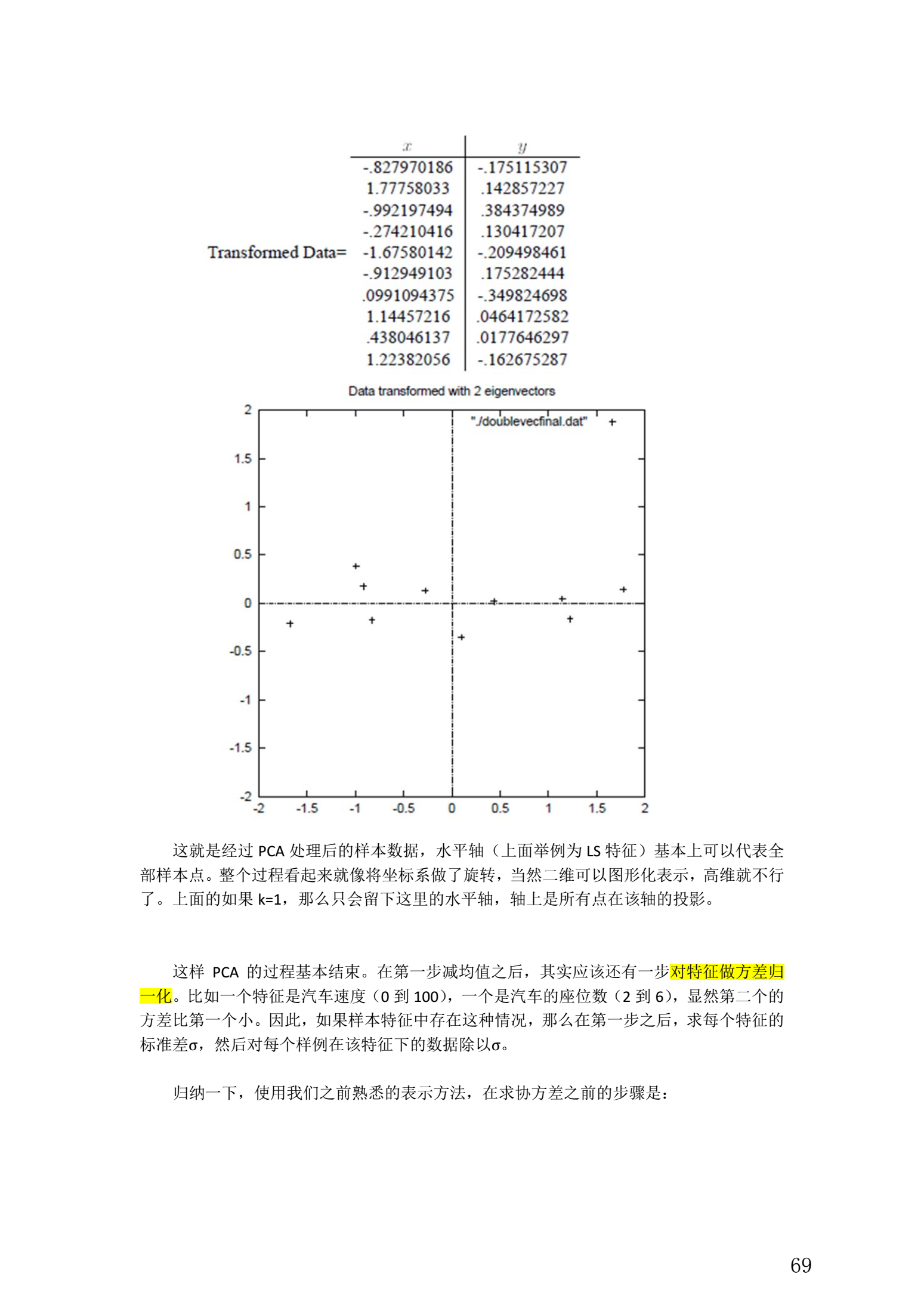
5. 总结与讨论

• PCA 技术的一大好处是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序，根据需要取前面最重要的部分，将后面的维数省去，可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。

• PCA 技术的一个很大的优点是，它是完全无参数限制的。在 PCA 的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预，最后的结果只与数据相关，与用户是独立的。　
• 但是，这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果，效率也不高。
• 在非高斯分布的情况下， PCA方法得出的主元可能并不是最优的

• 另外 PCA 还可以用于预测矩阵中缺失的元素