拓扑排序 Topological Sort

2018-05-02 16:26:07

一、拓扑排序

有向无环图（Directed acyclic graph，DAG）必定存在拓扑排序；非DAG没有拓扑排序一说。

二、拓扑排序算法

通常拓扑排序算法可以在O(n)的时间复杂度完成，具体来说是O(V + E)。

下面以leetcode207为例来介绍拓扑排序算法。

问题描述：

问题求解：

方法一、BFS

使用BFS求解拓扑排序是非常直观和简单的。

维护每个节点的indegree数目，对于入度为0的进队列，将所有入度为0的出队，并更新它们的邻接节点的indegree，若indegree == 0，入队。

循环以上操作直到队列为空。

    public boolean canFinish(int numCourses, int[][] prerequisites) {
        List<Integer>[] graph = new List[numCourses];
        int[] indegree = new int[numCourses];
        for (int i = 0; i < numCourses; i++) graph[i] = new ArrayList<>();
        for (int[] edge : prerequisites) {
            int from = edge[1];
            int to = edge[0];
            graph[from].add(to);
            indegree[to] += 1;
        }
        int cnt = 0;
        Queue<Integer> q = new LinkedList<>();
        for (int i = 0; i < numCourses; i++) {
            if (indegree[i] == 0) q.add(i);
        }
        while (!q.isEmpty()) {
            int curr = q.poll();
            cnt += 1;
            for (int next : graph[curr]) {
                indegree[next] -= 1;
                if (indegree[next] == 0) q.add(next);
            }
        }
        return cnt == numCourses;
    }

　　

方法二、DFS

使用DFS代码更为简洁。

实际就是给每个节点打上状态标签，如果访问到了正在访问的节点，那么必定存在环。

另外，我们需要一个访问完成的标签，避免重复访问已经访问过的节点。

    public boolean canFinish(int n, int[][] edges) {
        List<Integer>[] graph = new List[n];
        for (int i = 0; i < n; i++) graph[i] = new ArrayList<>();
        for (int[] e : edges) {
            int from = e[1];
            int to = e[0];
            graph[from].add(to);
        }
        int[] state = new int[n];
        for (int i = 0; i < n; i++) {
            if (state[i] == 0 && !dfs(graph, i, state)) return false;
        }
        return true;
    }

    private boolean dfs(List<Integer>[] graph, int node, int[] state) {
        state[node] = 1;
        for (int next : graph[node]) {
            if (state[next] == 2) continue;
            if (state[next] == 1) return false;
            if (!dfs(graph, next, state)) return false;
        }
        state[node] = 2;
        return true;
    }

三、拓扑排序应用

• 210. Course Schedule II

问题描述：

问题求解：

也是一条裸的拓扑排序题，相较于上一题，本题可以说是更纯粹的拓扑排序，因为不仅需要判环，还需要输出一个合法的解。当然，算法实现上也是两种思路，一是DFS，而是kahn算法。

DFS：

    public int[] findOrder(int numCourses, int[][] prerequisites) {
        int[] res = new int[numCourses];
        List<Integer>[] graph = new List[numCourses];
        for (int i = 0; i < numCourses; i++) graph[i] = new ArrayList<>();
        for (int[] pair : prerequisites) {
            graph[pair[1]].add(pair[0]);
        }
        int[] state = new int[numCourses];
        Stack<Integer> s = new Stack<>();
        for (int i = 0; i < numCourses; i++) {
            if (state[i] == 0)
                if (!dfs(graph, state, s, i)) return new int[0];
        }
        for (int i = 0; i < numCourses; i++) res[i] = s.pop();
        return res;
    }

    private boolean dfs(List<Integer>[] g, int[] state, Stack<Integer> s, int i) {
        if (state[i] == 2) return true;
        if (state[i] == 1) return false;
        state[i] = 1;
        for (int node : g[i]) {
            if (!dfs(g, state, s, node)) return false;
        }
        state[i] = 2;
        s.push(i);
        return true;
    }

Kahn：

    public int[] findOrder(int numCourses, int[][] prerequisites) {
        int[] res = new int[numCourses];
        int[] indegree = new int[numCourses];
        List<Integer>[] graph = new List[numCourses];
        for (int i = 0; i < numCourses; i++) graph[i] = new ArrayList<>();
        for (int[] pair : prerequisites) {
            graph[pair[1]].add(pair[0]);
            indegree[pair[0]]++;
        }
        Queue<Integer> q = new LinkedList<>();
        for (int i = 0; i < numCourses; i++) {
            if (indegree[i] == 0)
                q.add(i);
        }
        int cnt = 0;
        while (!q.isEmpty()) {
            int p = q.poll();
            res[cnt++] = p;
            for (int node : graph[p]) {
                if (--indegree[node] == 0) q.add(node);
            }
        }
        if (cnt == numCourses) return res;
        else return new int[0];
    }

• 1203. Sort Items by Groups Respecting Dependencies

问题描述：

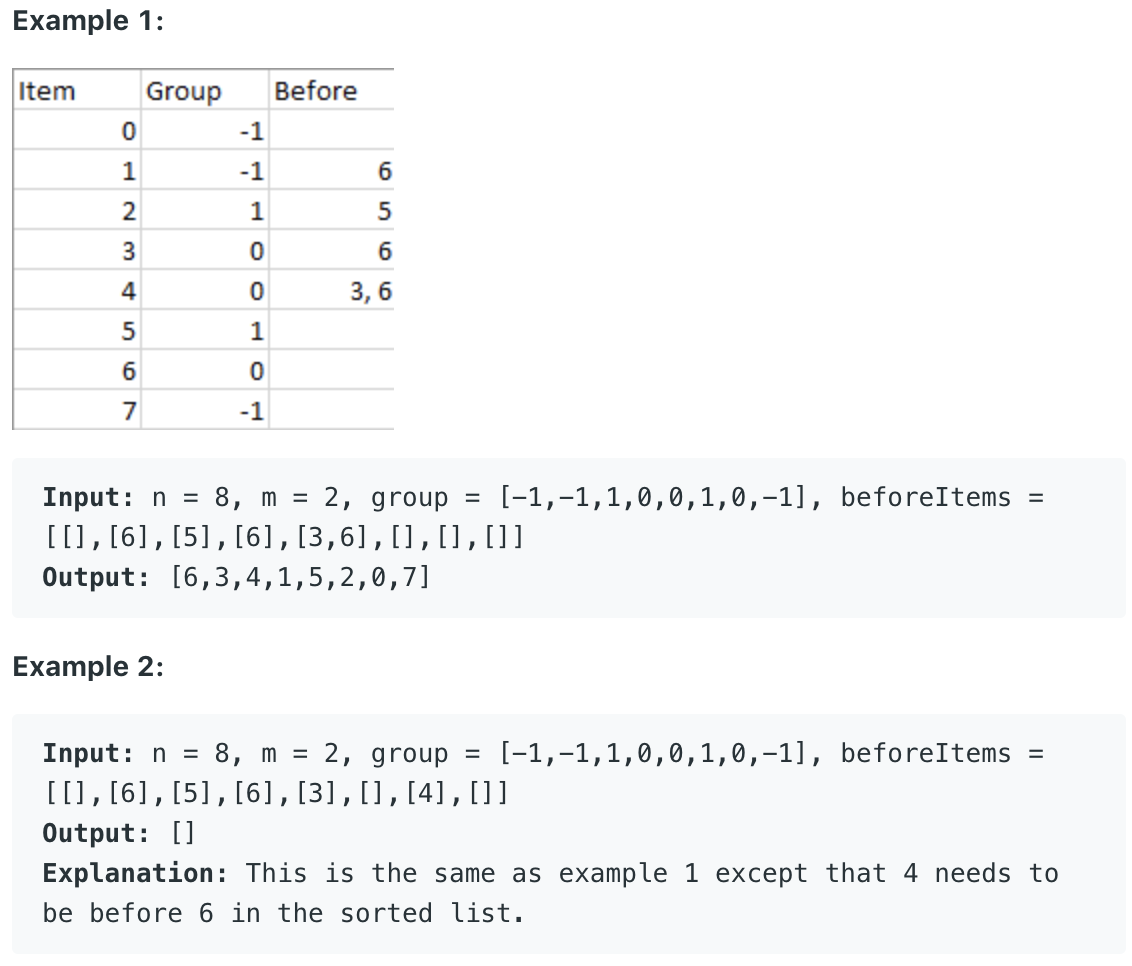
问题求解：

    public int[] sortItems(int n, int m, int[] group, List<List<Integer>> beforeItems) {
        Map<Integer, Set<Integer>> group2items = new HashMap<>();
        Map<Integer, Set<Integer>> group_g = new HashMap<>();
        Map<Integer, Integer> g_indegree = new HashMap<>();
        Map<Integer, Set<Integer>> item_g = new HashMap<>();
        Map<Integer, Integer> i_indegree = new HashMap<>();

        int num_of_groups = m;

        for (int i = 0; i < group.length; i++) {
            if (group[i] == -1) group[i] = num_of_groups++;
        }

        for (int i = 0; i < num_of_groups; i++) {
            group2items.put(i, new HashSet<>());
            group_g.put(i, new HashSet<>());
            g_indegree.put(i, 0);
        }

        for (int i = 0; i < n; i++) {
            item_g.put(i, new HashSet<>());
            i_indegree.put(i, 0);
            group2items.get(group[i]).add(i);
        }

        for (int to = 0; to < beforeItems.size(); to++) {
            int to_group = group[to];
            for (int from : beforeItems.get(to)) {
                int from_group = group[from];
                if (to_group == from_group) {
                    item_g.get(from).add(to);
                    i_indegree.put(to, i_indegree.get(to) + 1);
                }
                else {
                    if (!group_g.get(from_group).contains(to_group)) {
                        group_g.get(from_group).add(to_group);
                        g_indegree.put(to_group, g_indegree.get(to_group) + 1);
                    }
                }
            }
        }

        // check groups
        List<Integer> groups = new ArrayList<>();
        Queue<Integer> q = new LinkedList<>();
        for (int i = 0; i < num_of_groups; i++) {
            if (g_indegree.get(i) == 0) {
                q.add(i);
                groups.add(i);
            }
        }
        while (!q.isEmpty()) {
            int cur = q.poll();
            for (int to : group_g.get(cur)) {
                g_indegree.put(to, g_indegree.get(to) - 1);
                if (g_indegree.get(to) == 0) {
                    q.add(to);
                    groups.add(to);
                }
            }
        }
        if (groups.size() != num_of_groups) return new int[0];

        // check items
        List<Integer> res = new ArrayList<>();
        for (int g : groups) {
            int num = 0;
            q = new LinkedList<>();
            for (int item : group2items.get(g)) {
                if (i_indegree.get(item) == 0) {
                    q.add(item);
                    res.add(item);
                    num += 1;
                }
            }

            while (!q.isEmpty()) {
                int cur = q.poll();
                for (int to : item_g.get(cur)) {
                    i_indegree.put(to, i_indegree.get(to) - 1);
                    if (i_indegree.get(to) == 0) {
                        q.add(to);
                        res.add(to);
                        num += 1;
                    }
                }
            }
            if (num != group2items.get(g).size()) return new int[0];
        }
        int[] ret = new int[res.size()];
        for (int i = 0; i < res.size(); i++) ret[i] = res.get(i);
        return ret;
    }