数学归纳法·Fibonacci数列

数学归纳法

　　我们先来看一个例子：

我们让多诺米骨牌倒下的充要条件是：

1. 第一块骨牌倒下；
2. 假设当当前块骨牌倒下时，则他的后面一块也会倒下。

我们把这个例子给抽象出来就可以得到数学归纳法的证明过程：

【第一数学归纳法】证明一个关于正整数n的命题P(n)成立：

1. 当n=1时，P(1)成立。
2. 当n≥2时，假设P(n-1)成立，则可以推出P(n)成立。

【第二数学归纳法】证明一个关于正整数n的命题P(n)成立：

1. 证明一个或几个初值成立。
2. 假设n=k或n≤k（k∈N⁺）时命题成立，证明n=k+1时命题成立。

我们举一个例子来理解一下：

　　证明：1+2+3+…+n=(1/2)*n*(n+1)。

　　证明：当n=1时，显然成立。

　　　　　假设n=k（k≠1，k∈N⁺）时等式成立，那么当n=k+1时一定有：左边=（1+2+3+…+k）+（k+1）=（1/2）*k*（k+1）+（k+1）=（1/2）*（k+1）*（k+2）=右边

　　　　 　综上所述，得证。

二阶线性递归数列

定义

　　　　

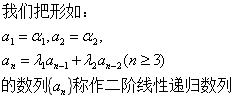
二阶线性递归数列的特征方程

　　　　

二阶线性递归数列的通项式推导

　　　　

Fibonacci数列

定义

　　　　

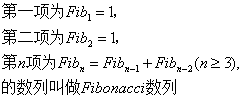
通项公式的证明

　　　　

Fibonacci数列的性质