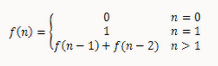剑指Offer面试题:7.斐波那契数列
一 题目:斐波那契数列
题目:写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项。斐波那契数列的定义如下:
二 效率很低的解法
很多C/C++/C#/Java语言教科书在讲述递归函数的时候,大多都会用Fibonacci作为例子,因此我们会对这种解法烂熟于心
#include "stdio.h"
#include <iostream>
using namespace std; int Fibs(int n)
{
if (0 == n)
{
return ;
}
else if (1 == n)
{
return ;
}
return Fibs(n-) + Fibs(n-);
} void main()
{
cout << "斐波那契数列:" << endl;
cout <<Fibs()<<" ";
cout <<Fibs()<<" ";
cout <<Fibs()<<" ";
cout <<Fibs()<<" ";
cout <<Fibs()<<" ";
cout <<Fibs()<<" ";
cout <<Fibs()<<" ";
cout <<Fibs()<<" ";
cout <<Fibs()<<" " << endl;
return;
}

上述递归的解法有很严重的效率问题,通过求解第10项的调用过程图来分析:

从上图中不难发现:在这棵树中有很多结点是重复的,而且重复的结点数会随着n的增大而急剧增加,这意味计算量会随着n的增大而急剧增大。事实上,用递归方法计算的时间复杂度是以n的指数的方式递增的。
三 时间复杂度为O(n)的解法
改进的方法并不复杂。上述递归代码之所以慢是因为重复的计算太多,我们只要想办法避免重复计算就行了。这里的办法是从下往上计算,首先根据f(0)和f(1)算出f(2),再根据f(1)和f(2)算出f(3)……依此类推就可以算出第n项了。很容易理解,这种思路的时间复杂度是O(n)。
#include "stdio.h"
#include <iostream>
using namespace std; int Fibs(int n)
{
int nFibs = ;
if ( == n)
{
return ;
}
else if( == n)
{
return ;
}
int nSubOne = ; // Fibs(n-1)
int nSubTwo = ; // Fibs(n-2)
for (int i = ; i <= n; i ++)
{
nFibs = nSubOne + nSubTwo;
nSubTwo = nSubOne;
nSubOne = nFibs;
} return nFibs;
} void main()
{
cout << "斐波那契数列:" << endl;
cout <<Fibs()<<" ";
cout <<Fibs()<<" ";
cout <<Fibs()<<" ";
cout <<Fibs()<<" ";
cout <<Fibs()<<" ";
cout <<Fibs()<<" ";
cout <<Fibs()<<" ";
cout <<Fibs()<<" ";
cout <<Fibs()<<" " << endl;
return;
}
剑指Offer面试题:7.斐波那契数列的更多相关文章
- 剑指Offer - 九度1387 - 斐波那契数列
剑指Offer - 九度1387 - 斐波那契数列2013-11-24 03:08 题目描述: 大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项.斐波那契数列的定义如下: ...
- 剑指offer第二版-10.斐波那契数列
面试题10:斐波那契数列 题目要求: 求斐波那契数列的第n项的值.f(0)=0, f(1)=1, f(n)=f(n-1)+f(n-2) n>1 思路:使用循环从下往上计算数列. 考点:考察对递归 ...
- 【剑指offer】9、斐波拉契数列
面试题9.斐波拉契数列 题目: 输入整数n,求斐波拉契数列第n个数. 思路: 一.递归式算法: 利用f(n) = f(n-1) + f(n-2)的特性来进行递归,代码如下: 代码: long long ...
- 剑指offer【07】- 斐波那契数列(java)
题目:斐波那契数列 考点:递归和循环 题目描述:大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0),n<=39. 法一:递归法,不过递归比较慢, ...
- 剑指offer(7)斐波那契数列
题目描述 大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项. n<=39 题目分析 我们都知道斐波那契可以用递归,但是递归重复计算的部分太多了(虽然可以通过),但是这 ...
- 【剑指Offer】7、斐波那契数列
题目描述: 大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0).假设n<=39. 解题思路: 斐波那契数列:0,1,1,2,3, ...
- 【剑指offer】7:斐波那契数列
题目描述: 大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0,第1项是1).假设 n≤39 解题思路: 斐波拉契数列:1,1,2,3,5,8--,总结 ...
- 剑指offer——矩阵覆盖(斐波那契变形)
****感觉都可以针对斐波那契写一个变形题目的集合了****** 我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形.请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法? cl ...
- 【剑指offer】面试题 10. 斐波那契数列
面试题 10. 斐波那契数列 题目一:求斐波那契数列的第n项 题目描述:求斐波拉契数列的第n项 写出一个函数,输入n,求斐波拉契(Fibonacci)数列的第n项.斐波拉契数列定义如下: C++ 实现 ...
- 剑指offer编程题Java实现——面试题9斐波那契数列
题目:写一个函数,输入n,求斐波那契数列的第n项. package Solution; /** * 剑指offer面试题9:斐波那契数列 * 题目:写一个函数,输入n,求斐波那契数列的第n项. * 0 ...
随机推荐
- iOS 多线程安全 与 可变字典
这周最大的收获是稍稍通透了 多线程安全字典的重要性. 诱因是,发现了有字典坏地址错误 果断以为是 value 或者 key 是可能出现了空值,补充了潜在的判断,虽然有的位置已经预判断的,但 ...
- python学习笔记:函数参数
1. 位置参数:一般的参数 2. 默认参数: def power(x, n=2): s = 1 while n > 0: n = n - 1 s = s * x return s 参数里有默认赋 ...
- 【Python】常用内建模块(卒)
内容来自廖雪峰的官方网站 笔记性质 1.datetime 2.collections 3.base64 4.struct 5.hashlib 6.itertools 7.contextlib 8.XM ...
- CSS3 文本常用属性
CSS 常用属性 text-shadow属性文字阴影:第一个值背景相对原本文字居左的距离,第二个值据当前文本上方的距离,第三个值清晰度(越小越清晰),第四个值颜色 word-wrap:自动换行,如果是 ...
- ssi include返回404页面
项目中index.html中包含<!--#include virtual="/commonfrag/djdzkan/recomm_www_info.inc" --> ...
- python3给socket模块设置代理
最近需要在公司学习socket编程,但是不能直接连接外网,需要设置一个代理才能正常访问.报错示例: import socket def blocking(wd): sock = socket.sock ...
- MYSQL提权的各种姿势
一.利用mof提权 前段时间Kingcope大牛发布了mysql远程提权0day,剑心牛对MOF利用进行了分析,如下: Windows 管理规范 (WMI) 提供了以下三种方法编译到 WMI 存储库的 ...
- IDEA 修改JSP和后端数据后,页面刷新可以实时更新
情况:刚开始使用IDEA进行开发时,发现修改JSP页面或者后端数据后,再刷新浏览器页面,发现没有变化,页面无更新. 这样就导致不得不频繁重启tomcat服务器.非常麻烦 解决方法: 步骤1. 先设置t ...
- windows 服务器恢复选项恢复
用户的服务器成了酱紫
- qtjambi_ZC
loadJambiJniLibrary --> loadLibrary --> loadNativeLibrary --> loadLibrary_helper class QApp ...