BZOJ5286：[HNOI/AHOI2018]转盘——题解

https://www.lydsy.com/JudgeOnline/problem.php?id=5286

https://www.luogu.org/problemnew/show/P4425

https://loj.ac/problem/2495

题面见上面。

然后因为懒得写公式了所以看这个人的博客吧：https://www.luogu.org/blog/litble-blog/solution-p4425

合并的原理如果看了那个博客还没看懂的话，不妨看看下面这张图：

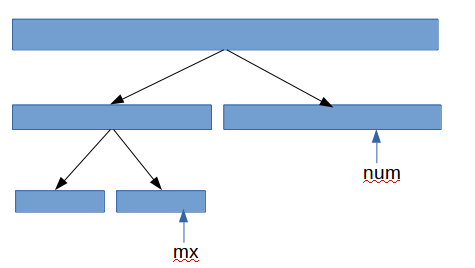
我们要求的是最上面区间的答案，但显然不能是tr[a]=min(tr[a<<1]],tr[a<<1|1])，因为中间的区间还需要合并。

因为参考博客已经证明了tr[a]表示的区间长度对答案没有影响了所以我们就考虑所有的区间即可。

我们的suan函数的a是最上边区间的左区间，mx和num就是当前区间的mx[a]。

显然当mx>=num的时候a的左区间答案只受mx的影响，而右区间的靠右位置有可能不受mx的影响，因此递归处理。

当mx<num的时候a的右区间只受num的影响，取一个最小值为mid+1+num，再递归处理左区间即可（因为左区间的mx可能比num大）。

#include<cmath>
#include<queue>
#include<vector>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=2e5+;
inline int read(){
    int X=,w=;char ch=;
    while(!isdigit(ch)){w|=ch=='-';ch=getchar();}
    while(isdigit(ch))X=(X<<)+(X<<)+(ch^),ch=getchar();
    return w?-X:X;
}
int n,m,p,t[N],b[N],tr[N*],mx[N*];
int suan(int a,int l,int r,int num){
    if(l==r)return l+max(mx[a],num);
    int mid=(l+r)>>;
    if(mx[a<<|]>=num)
    return min(tr[a],suan(a<<|,mid+,r,num));
    else return min(suan(a<<,l,mid,num),mid++num);
}
void upt(int a,int l,int r){
    mx[a]=max(mx[a<<],mx[a<<|]);
    tr[a]=suan(a<<,l,(l+r)>>,mx[a<<|]);
}
void build(int a,int l,int r){
    if(l==r){
    tr[a]=t[l];mx[a]=b[l];
    return;
    }
    int mid=(l+r)>>;
    build(a<<,l,mid);build(a<<|,mid+,r);
    upt(a,l,r);
}
void mdy(int a,int l,int r,int x){
    if(l==r){
    tr[a]=t[l];mx[a]=b[l];
    return;
    }
    int mid=(l+r)>>;
    if(x<=mid)mdy(a<<,l,mid,x);
    else mdy(a<<|,mid+,r,x);
    upt(a,l,r);
}
int main(){
    n=read(),m=read(),p=read();
    for(int i=;i<=n;i++){
    t[i]=t[i+n]=read();
    b[i]=t[i]-i;
    b[i+n]=t[i+n]-i-n;
    }
    build(,,n<<);
    int lastans=tr[]+n-;printf("%d\n",lastans);
    for(int i=;i<=m;i++){
    int x=read(),y=read();
    if(p)x^=lastans,y^=lastans;
    t[x]=t[x+n]=y;b[x]=y-x;b[x+n]=y-x-n;
    mdy(,,n<<,x);mdy(,,n<<,x+n);
    lastans=tr[]+n-;printf("%d\n",lastans);
    }
    return ;
}

+++++++++++++++++++++++++++++++++++++++++++

+本文作者：luyouqi233。 　　　　　　　　　　　　　　+

+欢迎访问我的博客：http://www.cnblogs.com/luyouqi233/+

+++++++++++++++++++++++++++++++++++++++++++