[洛谷P3629] [APIO2010]巡逻

洛谷题目链接:[APIO2010]巡逻

题目描述

在一个地区中有 n 个村庄，编号为 1, 2, ..., n。有 n – 1 条道路连接着这些村 庄，每条道路刚好连接两个村庄，从任何一个村庄，都可以通过这些道路到达其 他任一个村庄。每条道路的长度均为 1 个单位。 为保证该地区的安全，巡警车每天要到所有的道路上巡逻。警察局设在编号 为 1 的村庄里，每天巡警车总是从警察局出发，最终又回到警察局。 下图表示一个有 8 个村庄的地区，其中村庄用圆表示（其中村庄 1 用黑色的 圆表示），道路是连接这些圆的线段。为了遍历所有的道路，巡警车需要走的距 离为 14 个单位，每条道路都需要经过两次。

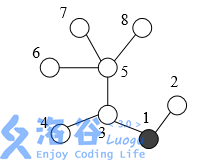
为了减少总的巡逻距离，该地区准备在这些村庄之间建立 K 条新的道路， 每条新道路可以连接任意两个村庄。两条新道路可以在同一个村庄会合或结束 （见下面的图例（c））。 一条新道路甚至可以是一个环，即，其两端连接到同一 个村庄。 由于资金有限，K 只能是 1 或 2。同时，为了不浪费资金，每天巡警车必须 经过新建的道路正好一次。 下图给出了一些建立新道路的例子：

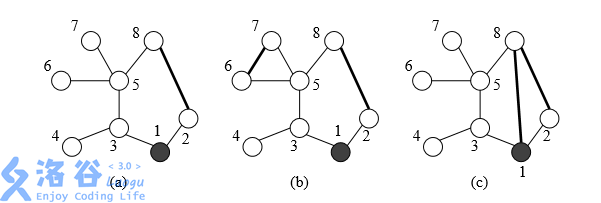
在(a)中，新建了一条道路，总的距离是 11。在(b)中，新建了两条道路，总 的巡逻距离是 10。在(c)中，新建了两条道路，但由于巡警车要经过每条新道路 正好一次，总的距离变为了 15。 试编写一个程序，读取村庄间道路的信息和需要新建的道路数，计算出最佳 的新建道路的方案使得总的巡逻距离最小，并输出这个最小的巡逻距离。

输入输出格式

输入格式：

第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1 行，每行两个整数 a, b， 表示村庄 a 与 b 之间有一条道路(1 ≤ a, b ≤ n)。

输出格式：

输出一个整数，表示新建了 K 条道路后能达到的最小巡逻距离。

输入输出样例

输入样例#1：

8 1

1 2

3 1

3 4

5 3

7 5

8 5

5 6

输出样例#1：

11

输入样例#2：

8 2

1 2

3 1

3 4

5 3

7 5

8 5

5 6

输出样例#2：

10

输入样例#3：

5 2

1 2

2 3

3 4

4 5

输出样例#3：

6

说明

10%的数据中，n ≤ 1000, K = 1；

30%的数据中，K = 1；

80%的数据中，每个村庄相邻的村庄数不超过 25；

90%的数据中，每个村庄相邻的村庄数不超过 150； 100%的数据中，3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。

一句话题意: 给出一颗树,你可以在树中加入\(k\)条边,且加入的边只能经过一次,问从\(1\)节点出发,到达每个点\(1\)次,至少需要走多远的距离.

题解: 首先发现\(k\)的范围非常小,可以考虑从这个入手,我们采用分类讨论的方式来分析一下.

首先考虑如果\(k=0\),因为树上两个点只有一条路径,所以如果要到每一个点并回来的话,需要的步数就是\((n-1)*2\)步.

也可以从欧拉回路的角度来理解一下上面讲的东西,每个点的度数都是\(2\)的倍数,说明一定是可以从一个点出发到所有点并回来的,而因为树上没有环,走到哪里就必须从哪里回来,所以要到每一个点就要将每条边遍历\(2\)遍.

然后我们在来想\(k=1\)的情况:现在新加入了一条边,那么显然此时就不是一颗树了,现在树上必定有一个环.而因为有了这个环,那么这个环上的边都是只需要遍历一遍的.所以根据贪心的思想,我们肯定是要这个环上的边尽量多,也就是连之前连的那条链尽量长,也就是树的直径.减去这个环上少走的边数再加上我们重新连的边长度,此时答案为\((n-1)*2-len1+1\),其中\(len1\)为这次求得的直径长度.

接下来我们需要求解\(k=2\)的情况,我们可以继续用之前分析\(k=1\)的情况的时候用的方法来处理\(k=2\)的情况.但是如果直接重新求一遍直径肯定是不行的,因为这一次选择连一条边之后有可能形成的环和之前形成的环上有重复的边,而这个长度是不能重复算入总答案中的.

又因为题目中说到新加入的边是只能走一次并且必须走一次的,所以其实在分析过\(k=1\)的情况后就不需要再知道之前连边的信息了,因为重新连一条边与之前的连边位置是没有关系的,最多只会影响两次在树上边的经过次数.

那么我们来分析一下如果第二次加边后的答案应该如何计算,显然为了答案最大,第二次加边后的答案是\((n-1)*2-len1+1-len2+1-len3\).其中\(len2\)为这次求得的直径大小,\(len3\)为这次直径与上次求的直径的重叠的部分.

然而我们在求直径的时候并不能求出这条直径与另一条直径相交的长度,所以我们可以在上次求出直径后直接将直径上经过的所有边的权值改为\(-1\),这样在下次求直径的时候就避免了求重复长度的问题了.

然后因为有负权边,所以在求解树的直径的时候要用\(DP\)的方式来求.

#include<bits/stdc++.h>
using namespace std;
const int N = 100000+5;

int n, k, ecnt = 1, last[N], ans, len0 = 0, len1 = 0, dep[N], f[N], pre[N], fa[N], L, R;

struct edge{
    int to, w, nex;
}e[N*2];

void add(int x, int y, int z){
    e[++ecnt].to = y, e[ecnt].w = z, e[ecnt].nex = last[x], last[x] = ecnt;
}

void dfs(int x, int las, int deep){
    dep[x] = deep, fa[x] = las;
    for(int to, i=last[x];i;i=e[i].nex){
        to = e[i].to; if(to == las) continue;
        dfs(to, x, deep+1);
        if(len0 < f[x]+f[to]+e[i].w) len0 = f[x]+f[to]+e[i].w, L = pre[x], R = pre[to];
        if(f[x] < f[to]+e[i].w) f[x] = f[to]+e[i].w, pre[x] = pre[to];
    }
}

void tag(int x, int y){
    if(dep[x] < dep[y]) swap(x, y);
    while(dep[x] > dep[y]){
        for(int i=last[x];i;i=e[i].nex)
            if(e[i].to == fa[x]) e[i].w = e[i^1].w = -1;
        x = fa[x];
    }
    if(x == y) return;
    while(x != y){
        for(int i=last[x];i;i=e[i].nex)
            if(e[i].to == fa[x]) e[i].w = e[i^1].w = -1;
        for(int i=last[y];i;i=e[i].nex)
            if(e[i].to == fa[y]) e[i].w = e[i^1].w = -1;
        x = fa[x], y = fa[y];
    }
}

void dfs2(int x){
    for(int to, i=last[x];i;i=e[i].nex){
        to = e[i].to; if(to == fa[x]) continue;
        dfs2(to);
        if(len1 < f[x]+f[to]+e[i].w) len1 = f[x]+f[to]+e[i].w;
        if(f[x] < f[to]+e[i].w) f[x] = f[to]+e[i].w;
    }
}

int main(){
    ios::sync_with_stdio(false);
    int x, y; cin >> n >> k, ans = (n-1)*2;
    for(int i=1;i<=n;i++) pre[i] = i;
    for(int i=1;i<n;i++) cin >> x >> y, add(x, y, 1), add(y, x, 1);
    dfs(1, -1, 1);
    if(k == 1) cout << ans-len0+1 << endl, exit(0);
    memset(f, 0, sizeof(f)), tag(L, R), dfs2(1);
    cout << ans-len0+1-len1+1 << endl;
    return 0;
}