详细理解平衡二叉树AVL与Python实现

前言

上一篇文章讨论的二叉搜索树，其时间复杂度最好的情况下是O(log(n))，但是最坏的情况是O(n)，什么时候是O(n)呢？

像这样：

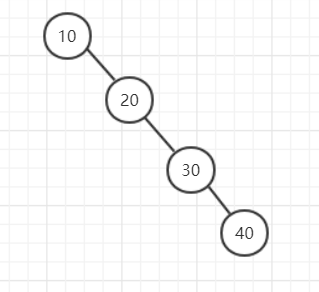
如果先插入10，再插入20，再插入30，再插入40就会成上边这个样子

这个就像是双向链表，我们期望它是下面这个样子：

所以我们希望有一种策略能够将第一个图变成第二个图，或者说使树的结构不会产生像第一种图的形式

实现这种策略的一种方式是AVL树

AVL树

AVL树的名称是以它的发明家的名字命名的：Adel’son-Vel’skii和Landis

满足高度平衡属性的二叉树就是AVL树

高度平衡属性是：对于树中的每一个位置p，p的孩子的高度最多相差1

很显然前言中的第一个图并不满足高度平衡属性，第二个是满足的。

同时高度平衡属性也意味着一颗AVL树的子树同样是AVL树

并且可以通过证明(这里就不再证了)得到AVL树的高度是O(log n)

所以得出结论，AVL树可以使时间复杂度保持O(log n)

接下来的问题就是怎样保持二叉树的高度平衡属性

保持二叉树的高度平衡属性

要保持高度平衡属性的原因是破坏了高度平衡属性

破坏的方式有两种：添加节点与删除节点

添加节点如图：

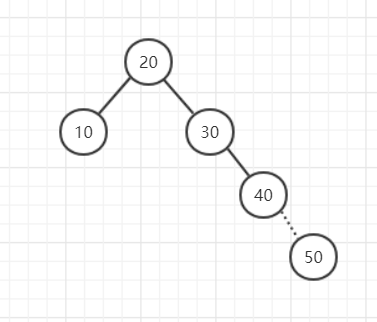
添加50的时候，就会破坏高度平衡属性

删除节点如图：

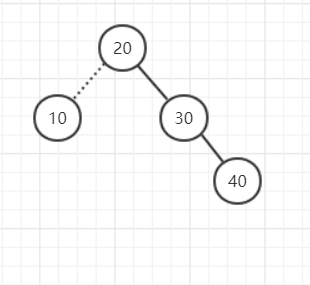
删除10的时候也会破坏高度平衡属性

最后，不论是添加节点还是删除节点，都会使树变成非高度平衡的状态，这种非高度平衡的状态有4种：

1.LL

LL是left-left，可以理解为：首先它不平衡，其次根节点的左子树比右子树高，并且根节点的左子树的左子树比根节点的左子树的右子树高。（从上到下都是左边高）

2.LR

LR是left-right，可以理解为：首先它不平衡，其次根节点的左子树比右子树高，并且根节点的左子树的右子树比根节点的左子树的左子树高。（从上到下先左高后右高）

3.RR

RR是right-right，可以理解为：首先它不平衡，其次根节点的右子树比左子树高，并且根节点的右子树的右子树比根节点的右子树的左子树高。（从上到下都是右边高）

4.RL

RL是right-left，可以理解为：首先它不平衡，其次根节点的右子树比左子树高，并且根节点的右子树的左子树比根节点的右子树的右子树高。（从上到下先右高后左高）

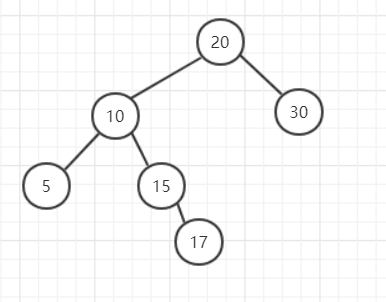
最后，判断是哪种形式的非平衡状态，一定要从不平衡的节点位置看，并不是看4层，比如：

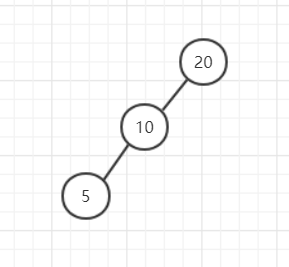
这里只有3层节点，不平衡的节点是20，20的左子树比右子树高，10的左子树比右子树高，所以是LL。（这里的高定义为节点5的高度为1，空节点的高度为0）

接下来是保持高度平衡的调整策略：

同样对于4种不同的形式有4种解决方案：

1.LL

这个变换就像是以10为中心，向右旋转，使10变成根节点，10的左子树不变，右子树变成了20，多余出的15正好挂在由于变换失去了左子树的20的左边。变换后结点从左到右的顺序依然没有变，所以15是正好挂在20的左边的。

2.RR

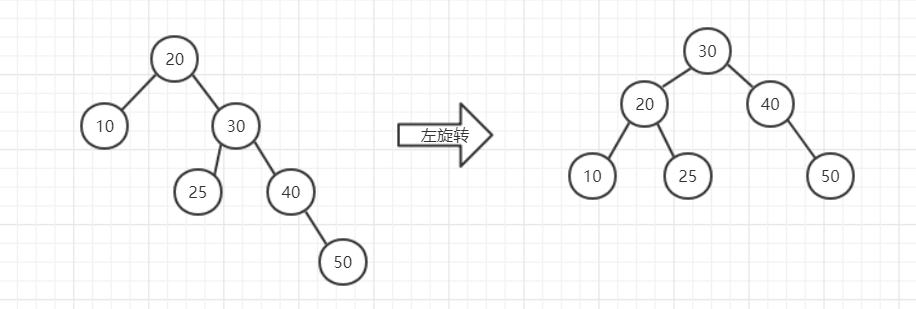
RR与LL形式差不多，只不顾是反着来的。相当于进行一次左旋转。

RR与LL都只进行一次旋转即可，而LR与RL需要进行两次旋转

3.LR

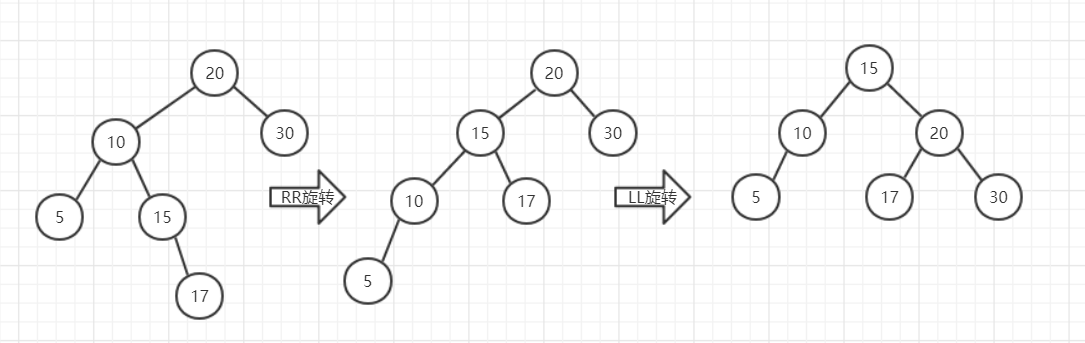
第一次相当于对5、10、15、17这棵子树进行了一次RR旋转，旋转方式与之前的RR方式相同，就像是以15为中心向左旋转，旋转的结果使得整棵树变成了LL的不平衡形态，然后再按照LL的旋转方式对整棵树处理。

4.RL

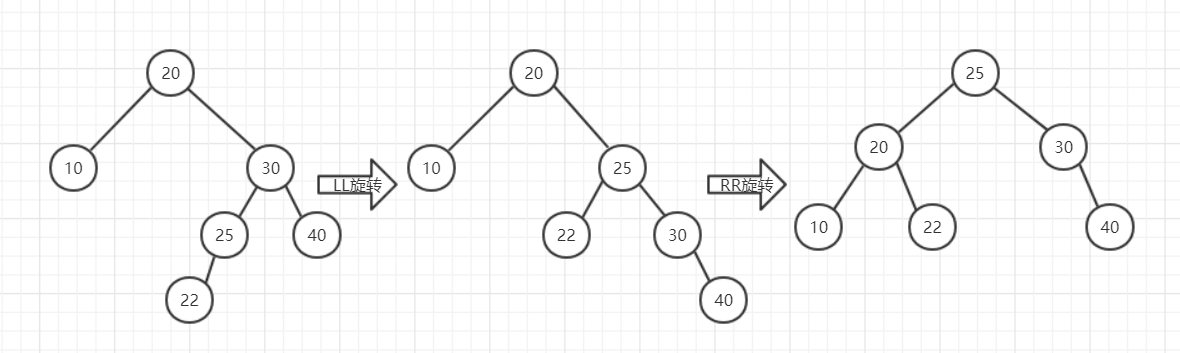
RL同样是LR的相反模式，先将22、25、30、40这棵子树进行LL旋转，再将整棵树进行RR旋转

理解了avl保持平衡从方式后，就可以用代码来实现了

Python实现

我们使用AVL对上一篇文章中的有序映射进行优化

因为AVL依赖于节点的高度，所以首先要重写一下Node类:

class AvlTree(OrderedMap):

    class Node(OrderedMap.Node):
        def __init__(self, element, parent=None, left=None, right=None):
            super().__init__(element,parent,left,right)
            self.height = 0

        def left_height(self):
            return self.left.height if self.left is not None else 0

        def right_height(self):
            return self.right.height if self.right is not None else 0

接下来定义4中调整的非公开方法

def _left_left(self,p):
    this = p.node        # 有变化的就4个节点
    left = this.left
    parent = this.parent
    left_right = this.left.right
    if parent is not None:
        if this is parent.left:
            parent.left = left
        else:
            parent.right = left
    else:
        self._root = left
    this.parent = left
    left.parent = parent
    this.left = left_right
    left.right = this
    if left_right is not None:
        left_right.parent = this

def _right_right(self,p):
    this = p.node                 # 有变化的就4个节点
    right = this.right
    parent = this.parent
    right_left = this.right.left
    if parent is not None:
        if this is parent.left:
            parent.left = right
        else:
            parent.right = right
    else:
        self._root = right
    this.parent = right
    right.parent = parent
    this.right = right_left
    right.left = this
    if right_left is not None:
        right_left.parent = this

def _left_right(self,p):
    self._right_right(self.left(p))
    self._left_left(p)

def _right_left(self,p):
    self._left_left(self.right(p))
    self._right_right(p)

然后是用于平衡二叉树的方法，也就是根据情况调用上边那4种策略

def _isbalanced(self,p):
    """判断节点是否平衡"""

    return abs(p.node.left_height() - p.node.right_height()) <= 1

def _recompute_height(self,p):
    """重新计算高度"""
    p.node.height = 1 + max(p.node.left_height(),p.node.right_height())

def _rebalanced(self,p):
    while p is not None:
        if self._isbalanced(p):
            self._recompute_height(p)
            p = self.parent(p)
        else:

            if p.node.left_height()>p.node.right_height() and p.node.left.left_height()>p.node.left.right_height():
                # LL的情况，只有自己和左孩子的高度可能变化
                self._left_left(p)
            elif p.node.right_height()>p.node.left_height() and p.node.right.right_height()>p.node.right.left_height():
                # RR的情况，只有自己和右孩子的高度可能变化
                self._right_right(p)
            elif p.node.left_height()>p.node.right_height() and p.node.left.left_height()<p.node.left.right_height():
                # LR的情况，只有自己和左孩子和左孩子的右孩子的高度可能变化
                left = self.left(p)
                self._left_right(p)
                self._recompute_height(left)
            else:
                # RL的情况，只有自己和右孩子和右孩子的左孩子的高度可能变化
                right = self.right(p)
                self._right_left(p)
                self._recompute_height(right)
            while p is not None:
                # 调整所有p的祖先的高度
                self._recompute_height(p)
                p = self.parent(p)

然后把方法封装成删除时和插入时的两个方法，虽然执行的内容是相同的

def _rebalanced_insert(self,p):
    """插入时的平衡调整"""
    self._rebalanced(p)

def _rebalanced_delete(self, p):
    """删除时的平衡调整"""
    self._rebalanced(p)

最后重写一下setitem方法与删除时调用的方法

def __setitem__(self, k, v):
    """优化setitem"""
    if self.is_empty():
        leaf = self.add_root(self._Item(k, v))
    else:

        p = self._subtree_search(self.root(), k)
        if p.key() == k:
            p.element().value = v
            return
        else:
            item = self._Item(k, v)
            if p.key() < k:
                leaf = self.add_right(p, item)
            else:
                leaf = self.add_left(p, item)
    self._rebalanced_insert(leaf)

def mapdelete(self, p):
    if self.left(p) and self.right(p):  # 两个孩子都有的时候
        replacement = self._subtree_last_position(
            self.left(p))  # 用左子树最右位置代替
        self.replace(p, replacement.element())
        p = replacement
    parent = self.parent(p)
    self.delete(p)
    self._rebalanced_delete(parent)

在实现4种平衡策略时，一定要记着将整棵树的根节点更新，不然遍历的时候，根节点指的就不是真正的根节点了。

​