洛谷P3515 [POI2011]Lightning Conductor（动态规划，决策单调性，单调队列）

洛谷题目传送门

疯狂%%%几个月前就秒了此题的Tyher巨佬

借着这题总结一下决策单调性优化DP吧。蒟蒻觉得用数形结合的思想能够轻松地理解它。

首先，题目要我们求所有的\(p_i\)，那么把式子变一下

\[p_i\ge a_j-a_i+\sqrt{|i-j|}
\]

\[p_i=\max\limits_{j=1}^n\{a_j+\sqrt{|i-j|}\}-a_i
\]

绝对值看着很不爽，我们把它拆开

\[p_i=\max(\max_{j=1}^i\{a_j+\sqrt{i-j}\},\max_{j=i}^n\{a_j+\sqrt{j-i}\})-a_i
\]

单独看前一部分

\[p_i=\max_{j=1}^i\{a_j+\sqrt{i-j}\}-a_i
\]

很明显是个要用决策单调性优化的式子。把序列翻转以后，后一部分的算法和前面是一样的，所以只讨论前一部分了。

对于每个\(j\)，把\(a_j+\sqrt{i-j}\)看成关于\(i\)的函数\(f_j\)。我们要做的就是在所有\(j\leq i\)的函数中找到最值。比如样例：

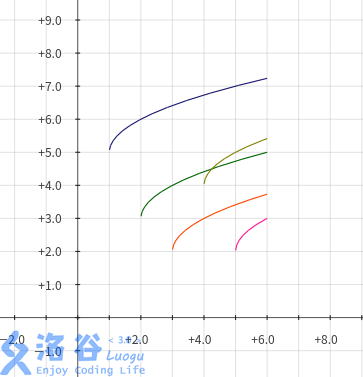
观察发现，真正有用的函数只有最上面那个！然而实际情况比这个稍复杂些。sqrt的增速是递减的，因此可能存在一个\(j\)比较小的函数，在某一时刻被\(j\)比较大的函数反超。我们大概需要维护这样的若干个函数：

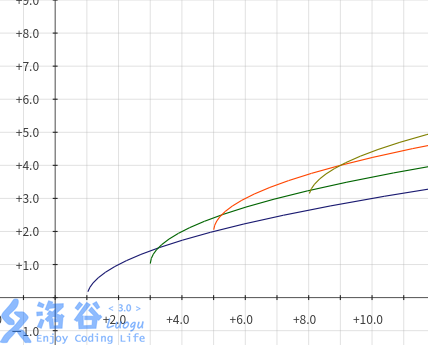
我们用队列实现决策二分栈（不懂的可以参考一下蒟蒻的blog），按\(j\)从小到大依次维护这些函数。显然，对于其中任意两个相邻的函数\(f_t,f_{t+1}\)，它们都有一个临界值\(k_{t,t+1}\)。显然序列中的\(k_{1,2},k_{2,3}...\)也要严格递增。否则，如果\(k_{t,t+1}\ge k_{t+1,t+2}\)，可以想象\(f_{t+1}\)根本没有用。

先for一遍\(i\)，我们尝试着把\(f_i\)加入队列。这时候为了保证\(k\)递增，设队尾决策为\(t\)，我们判断，如果\(k_{t-1,t}\ge k_{t,i}\)（此时会有\(f_t(k_{t-1,t})\le f_i(k_{t-1,t})\)），那么\(t\)没用，出队。

该出去的都出去后，\(i\)就可以加入队尾了。这时候可以来求\(p_i\)了。我们检查一下队首决策\(h\)，如果\(t_{h,h+1}\le i\)，说明\(h\)的巅峰时刻已经过去，出队。最后队首就是所有函数中的最大值。

貌似并没有用到什么三元组啊qwq

update:感谢孤独·粲泽的指正，二分上下界确实该调调

不过还是没有用到什么三元组啊qwq，蒟蒻之前都把临界值\(k\)存下了，直接用就可以啦

#include<bits/stdc++.h>
#define RG register
#define R RG int
#define G if(++ip==iend)fread(ip=buf,1,N,stdin)
#define calc(i,j) a[j]+sq[i-j]//计算函数值
using namespace std;
const int N=5e5+9;
char buf[N],*iend=buf+N,*ip=iend-1;
int n,a[N],q[N],k[N];
double p[N],sq[N];
inline int in(){
    G;while(*ip<'-')G;
    R x=*ip&15;G;
    while(*ip>'-'){x*=10;x+=*ip&15;G;}
    return x;
}
inline void chkmx(RG double&x,RG double y){
    if(x<y)x=y;
}
inline int bound(R x,R y){//二分临界值k
    R l=y,r=k[x]?k[x]:n,m,ret=r+1;//控制二分上下界
    while(l<=r){
        m=(l+r)>>1;
        if(calc(m,x)<=calc(m,y))
            ret=m,r=m-1;
        else l=m+1;
    }
    return ret;
}
void work(){
    for(R h=1,t=0,i=1;i<=n;++i){
        while(h<t&&calc(k[t-1],q[t])<calc(k[t-1],i))--t;//维护k单调
        k[t]=bound(q[t],i);q[++t]=i;
        while(h<t&&k[h]<=i)++h;//将已经不优的决策出队
        chkmx(p[i],calc(i,q[h]));//因为做两遍所以取max
    }
}
int main(){
    n=in();
    R i,j;
    for(i=1;i<=n;++i)
        a[i]=in(),sq[i]=sqrt(i);
    work();
    for(i=1,j=n;i<j;++i,--j)//序列翻转
        swap(a[i],a[j]),swap(p[i],p[j]);
    work();
    for(R i=n;i;--i)//翻转过了所以要倒着输出
        printf("%d\n",max((int)ceil(p[i])-a[i],0));
    return 0;
}