最短路：spfa算法

板子补完计划绝赞继续中(

这篇博客就来写一写spfa（这我居然板子都打错了一次，我太弱啦！）

先来看一下定义：（引自http://blog.csdn.net/juststeps/article/details/8772755）

首先说明，SPFA是一种单源最短路径算法，所以以下所说的“某点的最短路径长度”，指的是“某点到源点的最短路径长度”。

我们记源点为S，由源点到达点i的“当前最短路径”为D[i]，开始时将所有D[i]初始化为无穷大，D[S]则初始化为0。算法所要做的，就是在运行过程中，不断尝试减小D[]数组的元素，最终将其中每一个元素减小到实际的最短路径。

过程中，我们要维护一个队列，开始时将源点置于队首，然后反复进行这样的操作，直到队列为空：

(1)从队首取出一个结点u，扫描所有由u结点可以一步到达的结点，具体的扫描过程，随存储方式的不同而不同；

(2)一旦发现有这样一个结点，记为v，满足D[v] > D[u] + w(u, v)，则将D[v]的值减小，减小到和D[u] + w(u, v)相等。其中，w(u, v)为图中的边u-v的长度，由于u-v必相邻，所以这个长度一定已知（不然我们得到的也不叫一个完整的图）；这种操作叫做松弛。

引用内容
松弛操作的原理是著名的定理：“三角形两边之和大于第三边”，在信息学中我们叫它三角不等式。所谓对i,j进行松弛，就是判定是否d[j]>d[i]+w[i,j]，如果该式成立则将d[j]减小到d[i]+w[i,j]，否则不动。

(3)上一步中，我们认为我们“改进了”结点v的最短路径，结点v的当前路径长度D[v]相比于以前减小了一些，于是，与v相连的一些结点的路径长度可能会相应地减小。注意，是可能，而不是一定。但即使如此，我们仍然要将v加入到队列中等待处理，以保证这些结点的路径值在算法结束时被降至最优。当然，如果连接至v的边较多，算法运行中，结点v的路径长度可能会多次被改进，如果我们因此而将v加入队列多次，后续的工作无疑是冗余的。这样，就需要我们维护一个bool数组Inqueue[]，来记录每一个结点是否已经在队列中。我们仅将尚未加入队列的点加入队列。

算法能否结束？

对于不存在负权回路的图来说，上述算法是一定会结束的。因为算法在反复优化各个最短路径长度，总有一个时刻会进入“无法再优化”的局面，此时一旦队列读空，算法就结束了。然而，如果图中存在一条权值为负的回路，就糟糕了，算法会在其上反复运行，通过“绕圈”来无休止地试图减小某些相关点的最短路径值。假如我们不能保证图中没有负权回路，一种“结束条件”是必要的。这种结束条件是什么呢？思考Bellman-Ford算法，它是如何结束的？显然，最朴素的Bellman-Ford算法不管循环过程中发生了什么，一概要循环|V|-1遍才肯结束。凭直觉我们可以感到，SPFA算法“更聪明一些”，就是说我们可以猜测，假如在SPFA中，一个点进入队列——或者说一个点被处理——超过了|V|次，那么就可以断定图中存在负权回路了。

定义从来就不是我们要学习的重点 我们要优雅の打板子！

   来看这一道比奶牛热浪还裸的模板题：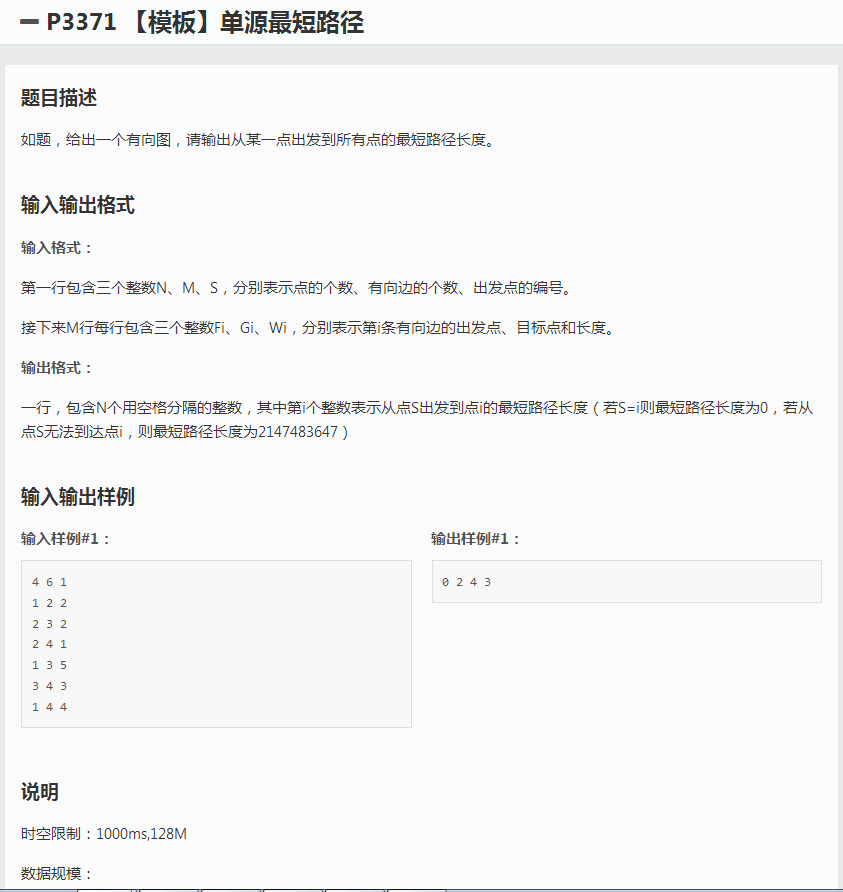

      然而似乎还是不够裸..

   我们让结构允许出现负环，出现时输出-1

   就可以用下面的代码实现啦

#pragma GCC optimize("O2")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<limits.h>
#include<ctime>
#define N 100001
typedef long long ll;
const int inf=0x3fffffff;
const int maxn=2017;
using namespace std;
inline int read()
{
    int f=1,x=0;char ch=getchar();
    while(ch>'9'||ch<'0')
    {
        if(ch=='-')
        f=-1;
        ch=getchar();
    }
    while(ch<='9'&&ch>='0')
    {
        x=(x<<3)+(x<<1)+ch-'0';
        ch=getchar();
    }
    return f*x;
}
struct tsdl{
	int to,w,next;
}edge[N*4];
int tot,head[N],inq[N],d[N],n,m,cnt[N];
queue<int>q;

void add(int ui,int vi,int wi)
{
	edge[++tot].next=head[ui];
	edge[tot].w=wi;
	edge[tot].to=vi;
	head[ui]=tot;
}
bool spfa(int u,int n)
{
    memset(inq,0,sizeof(inq));
    for(int i=1;i<=n;i++)
    d[i]=inf;
    d[u]=0,inq[u]=1;
    q.push(u);
    while(!q.empty())
    {
        int x=q.front();
        q.pop();
        inq[x]=0;
        for(int i=head[x];i!=-1;i=edge[i].next)
        {
            int v=edge[i].to;
            if(d[v]>d[x]+edge[i].w)
            {
                d[v]=d[x]+edge[i].w;
                if(!inq[v])
                {
                    inq[v]=1;
                    q.push(v);
                    if(++cnt[v]>n)return 1;
                }
            }
        }
    }
    return 0;
}

int main()
{
	memset(head,-1,sizeof(head));
	n=read(),m=read();
	int ts=read();
	for(int i=1;i<=m;i++)
	{
		int u=read(),v=read(),w=read();
		add(u,v,w);
	}
	if(spfa(ts,n))
	{
		cout<<-1<<endl;
		return 0;
	}
	for(int i=1;i<=n;i++)
        cout<<d[i]<<endl;
}

　　一期非常蒟蒻的模板总结 以上desu