OI内的排列与组合（简单版）

§1基本原理

△让我们来看下面问题：
　　从甲地到乙地，可以乘火车，也可以乘汽车，还可以乘轮船。一天中，火车有4班，汽车有2班，轮船有3班。那么，一天中乘坐这些交通工具从甲地到乙地共有多少种不同走法？
△分析：因为从甲地到乙地，乘火车有4种选择（方法），乘汽车有2种选择（方法），乘轮船有3种选择（方法）。因此，一天中乘坐这些交通工具从甲地到乙地共有：4＋2＋3 = 9种不同的方法。

▲一般地，做一件事，完成它可以有n类方法，在第一类办法中有m1种不同的方法，在第二类办法中有m2种不同的方法，……，在第n类办法中有m n种不同的方法，
那么完成这件事共有：N = m1＋m2＋…＋m n种不同的方法。

一、加法原理：
　　△再看这样一个例子：
　　　　由A村去Ｂ村的道路有３条，由Ｂ村去Ｃ村的道路有２条（如下图所示）。从Ａ村经Ｂ村去Ｃ村，共有多少种不同的走法？

　　　　△分析：从A村到B村有3种不同的走法，按这3种走法中的每一种走法到达B村后，再从B村到C村又有2种不同的走法。因此，从A村经B村去C村共有：3×2 = 6种不同的走法。

▲一般地，做一件事，完成它需要分成n个步骤，做完第一步有m1种不同的方法，做完第二步有m2种不同的方法，……，做第n步有m n种不同的方法。
那么，完成这件事共有：N = m1×m2×…×m n种不同的方法。

二、乘法原理：
　　〖举例〗
　　　　1． 书架上层放有6本不同的数学书，下层放有5本不同的语文书。
　　　　　　　　⑴从中任取一本，有多少种不同的取法？
　　　　　　　　⑵从中任取数学书与语文书各一本，有多少种不同的取法？
　　　　解：⑴分析：从书架上任取一本书，有两类情况：第1类情况是从上层取数学书，可以从6本书中任取一本，有6种方法；第2类情况是从下层取语文书，可以从5本书中任取一本，有5种方法。
　　　　　　　　根据加法原理，得到不同的取法的种数是： N = 6＋5 = 11
　　　　　　⑵分析：从书架中任取数学书与语文书各一本，可以分成两个步骤：第1步取一本数学书，有6种方法；第2步取一本语文书，有5种方法。
　　　　　　　　根据乘法原理，得到不同的取法的种数是：N = 6×5 = 30
　　　　2． 由数字1，2，3，4，5可以组成多少个三位数（各位上的数字允许重复）？
　　　　解：分析：要组成一个三位数可以分成三个步骤：　　　　　　　　　　

　　　　　　　　　　①第1步确定百位上的数字，从5个数字中任选一个数字，共有5种选法；　　　　　　　　　　

　　　　　　　　　　②第2步确定十位上的数字（由于数字允许重复）这儿仍有5种选法；　　　　　　　　　　

　　　　　　　　　　③第3步确定个位上的数字，同理，它也有5种选法。
　　　　　　　　根据乘法原理，得到可以组成的三位数的个数是：N = 5×5×5 = 5 3 = 125
　　▲不难发现，加法原理的要点是一个“类”字，乘法原理的要点是一个“步”字，即分“类”时用加法原理；分“步”时用乘法原理棗分清“类”与“步”是正确解题的关键。
　　△练习：
　　　　　　1．在读书活动中，一个学生要从2本科技书、2本政治书、3本文艺书里任选一本，共有多少种不同的选法？
　　　　　　2．乘积（a1＋a2＋a3）（b1＋b2＋b3＋b4）（c1＋c2＋c3＋c4＋c5）展开后共有多少项？
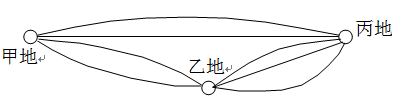
　　　　　　3．如下图所示，从甲地到乙地有2条陆路可走，从乙地到丙地有3条陆路可走，又从甲地不经过乙地到丙地有2条水路可走。
　　　　　　　　⑴从甲地经乙地到丙地有多少种不同的走法？
　　　　　　　　⑵从甲地到丙地共有多少种不同的走法？

                              

 

 

                                                         　　　　　　　　　　　　　　　§2排列　

△让我们来看下面这个例子：

　　由数字1，2，3，4可以组成多少个没有重复数字的三位数？

　　△分析：这个问题就是从1，2，3，4这四个数中，每次取出三个，按照百位、十位、个位的顺序排列起来，求一共有多少种不同的排法。

　　　　第一步：先确定百位上的数字，在1，2，3，4这四个数字中任取一个，有4种方法。

　　　　第二步：确定十位上的数字。当百位上的数字确定以后，十位上的数字只能从余下的三个数字中去取，有3种方法。

　　　　第三步：确定个位上的数字。当百位、十位上的数字都确定以后，个位上的数字只能从余下的两个数字中去取，有2种方法。

　　　　根据乘法原理，可以组成4×3×2 = 24 个没有重复数字的三位数。

▲上面这个问题实质是从4个不同的元素（通常，将被取的对象叫做元素）中，任取3个，然后按一定的顺序排成一列，求一共有多少种不同的排法。

 

一般地说，从n个不同元素中，任取m（m≤n）个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出m 个元素的一个排列。

 

一、排列：

▲从n个不同元素中取出m（m≤n）个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用图一所示符号表示。

〖举例〗从8个不同元素中取出5个元素的排列数图二所示符号表示 ，从7个不同元素中取出6个元素的排列数图三所示符号表示。

  图一　　   图二　      图三　　

二、排列数：

△让我们来看这样一个问题：求排列数P(2,n)。

　　分析：　⑴先填第一个位置，可以从这n个元素中任选一个填空，有n种方法。

　　　　　　⑵再填第二个位置，可以从剩下的n－1个元素中任选一个填空，有n－1种方法。

　　　　于是，根据乘法原理，得到排列数为 = n ( n－1)

　　　　类似，排列数 = n ( n－1 ) ( n－2 )。

三、排列数公式：P(m,n)= n ( n－1 ) ( n－2 ) … ( n－m＋1 )

　　这里n，m∈N，并且m≤n。

　　▲自然数1到n的边乘积，叫做n的阶乘，用n !表示。

　　△当m = n时，有P(m,n)= n • ( n－1 ) • ( n－2 ) … 3 • 2 • 1=n!　　

n个不同元素全部取出的一个排列，叫做n个不同元素的一个全排列

　　【举例】

　　　　1、某段铁路上有12个车站，共需要准备多少种普通客票？

　　　　　　解：△分析：因为每一张车票对应着2个车站的一个排列，因此需要准备的车票种数，就是从12个车站中任取2个的排列数。12×11=132 （种）

　　　　2、某信号兵用红、黄、蓝三面旗从上到下挂在竖直的旗杆上表示信号，每次可以任挂一面、二面或三面，并且不同的顺序表示不同的信号，一共可以表示多少种不同的信号？

　　　　　　解：△分析：如果把3面旗看成3个元素，则从3个元素里每次取出1个元素的一个排列，对应一种信号。

　　　　　　　　　　　　根据加法原理，所求的信号种数是3＋3×2＋3×2×1=15(种)

　　　　3、用0到9这十个数字，可以组成多少个没有重复数字的三位数？

　　　　　　　　△分析：百位上的数字只能从除0以外的1到9这九个数字中任选一个；十位和个位上的数字，可以从余下的九个数字中任选两个。

　　　　　　　　　　　　根据乘法原理，所求的三位数的个数是 9×9×8 = 648

　　△练习：

　　　　1.6名同学排成一排照相，有多少种排法？

　　　　2.有5本不同的书，准备给3名同学，每人1本，共有多少种给法？

　　　　3.一个火车站有8股岔道，停放4列不同的火车，有多少种不同的停放的方法（假定每股岔道只能停放一列火车）？

 

 

 

 

△让我们来看下面的例子：从5名学生中，选出2名去农村调查，有多少种选法？

　　△分析：这个问题可以理解为从5个元素中任取2个，不管怎样的顺序并成一组，求一共有多少个不同的组（从5名学生中选出2名学生，被选出的2名学生中谁先被选出、谁后被选出与求解无关）——这是组合问题了。

 

▲一般地说，从n个不同元素中，任取m（m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合。

一、组合：

　　△从5个不同元素a，b，c，d，e中取出2个元素的排列与组合的关系如下所示

　　组  合排  列

　　  a,b                a,b||b,a

　　  a,c                a,c||c,a

　　  a,d               a,d||d,a

　　  a,e               a,e||e,a

　　........................

　　不难发现，排列与元素的顺序有关，组合与元素顺序无关。

　　从n个不同元素中取出m（m≤n）个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数，用符号C(m,n)【其中m在C左上方，n在C左下方】表示。

二、组合数公式：

　　C(m,n)=P(m,n)/P(m,m)=n*(n-1)*....*(n-m+1)/(m!)

　　又∵P(m,n)=n!/(n-m)!

　　∴C(m,n)=n!/[m!*(n-m)!]

 

 

　　　　

　　2.

 

　　　　

　　　　

进行一个补充：

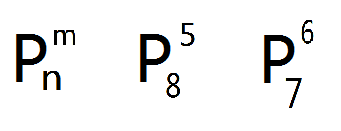
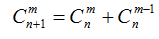
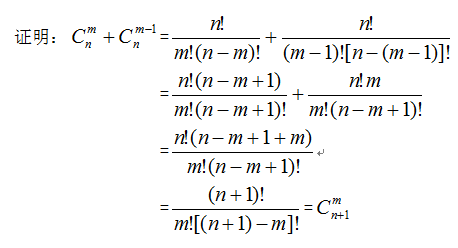
巧用“捆绑”、“插空”、“分组”法解决排列组合题目

在求解排列组合问题时，经常遇到有关几个元素必须相邻、几个元素互不相邻、将ｎ个元素分成ｍ组的问题。现将此类问题的解法通过例题介绍如下。
　　例１ 由数字１、２、３、４、５、６、７组成无重复数字的七位数。(1）求三个偶数必相邻的七位数的个数；（2）求三个偶数互不相邻的七位数的个数。
　　　　解 (1)：因为三个偶数２、４、６必须相邻，所以要得到一个符合条件的七位数可以分为如下三步：第一步将１、３、５、７四个数字排好有P(4,4)种不同的排法；
　　　　　　　　第二步将２、４、６三个数字“捆绑”在一起有P(3,3) 种不同的“捆绑”方法; 第三步将第二步“捆绑”的这个整体“插入”到第一步所排的四个不同数字的五个“间隙”(包括两端的两个位置)中的其中一个位置上,有P(1,5)种不同的“插入”方法。根据乘法原理共有P(4,4)*P(3,3)*P(5,1)=720种不同的排法。所以共有720个符合条件的七位数。
　　　　解（2）：因为三个偶数２、４、６ 互不相邻，所以要得到符合条件的七位数可以分为如下两步：第一步将１、３、５、７四个数字排好，有P(4,4) 种不同的排法；
　　　　　　　　第二步将２、４、６分别“插入”到第一步排的四个数字的五个“间隙”（包括两端的两个位置）中的三个位置上，有P(3,5) 种“插入”方法。根据乘法原理共有P(4,4)*P(3,5)＝1440种不同的排法。所以共有1440个符合条件的七位数。
　　例２ 将Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ分成三组，共有多少种不同的分法？
　　　　解：要将Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ分成三组，可以分为三类办法：（１－１－４）分法、（１－２－３）分法、（２－２－２）分法。下面分别计算每一类的方法数：
　　　　　　　　第一类（１－１－４）分法，这是一类整体不等分局部等分的问题，可以采用两种解法。解法一：从六个元素中取出四个不同的元素构成一个组，余下的两个元素各作为一个组，有C(4,6)种不同的分法。
　　　　解法二：从六个元素中先取出一个元素作为一个组有C(1,6) 种选法，再从余下的五个元素中取出一个元素作为一个组有C(1,5) 种选法，最后余下的四个元素自然作为一个组，由于第一步和第二步各选取出一个元素分别作为一个组有先后之分，产生了重复计算，应除以P(2,2)。所以共有C(1,6)*C(1,5)/P(2,2) ＝15种不同的分组方法。
　　　　　　　　第二类（１－２－３）分法，这是一类整体和局部均不等分的问题，首先从六个不同的元素中选取出一个元素作为一个组有C(1,6) 种不同的选法，再从余下的五个不同元素中选取出两个不同的元素作为一个组有C(2,5) 种不同的选法，余下的最后三个元素自然作为一个组，根据乘法原理共有C(1,6)*C(2,5)＝60种不同的分组方法。
　　　　　　　　第三类（２－２－２）分法，这是一类整体“等分”的问题，首先从六个不同元素中选取出两个不同元素作为一个组有C(2,6) 种不同的取法，再从余下的四个元素中取出两个不同的元素作为一个组有C(2,4)种不同的取法，最后余下的两个元素自然作为一个组。由于三组等分存在先后选取的不同的顺序，所以应除以P(3,3) ，因此共有C(2,6)*C(2,4)/P(3,3) ＝15种不同的分组方法。
根据加法原理，将Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ六个元素分成三组共有：15＋60＋15＝90种不同的方法。
　　例３ 一排九个坐位有六个人坐，若每个空位两边都坐有人，共有多少种不同的坐法？
　　　　解：九个坐位六个人坐，空了三个坐位，每个空位两边都有人，等价于三个空位互不相邻，可以看做将六个人先依次坐好有P(6,6)种不同的坐法，再将三个空坐位“插入”到坐好的六个人之间的五个“间隙”（不包括两端）之中的三个不同的位置上有C(3,5)种不同的“插入”方法。根据乘法原理共有P(6,6)*C(3,5)＝7200种不同的坐法。

小结：（１）ｍ个不同的元素必须相邻，有P(m,m) 种“捆绑”方法。
（２）ｍ个不同元素互不相邻，分别“插入”到ｎ个“间隙”中的ｍ个位置有 P(m,n)种不同的“插入”方法。
（３）ｍ个相同的元素互不相邻，分别“插入”到ｎ个“间隙”中的ｍ个位置，有C(m,n)种不同的“插入”方法。
（４）若干个不同的元素“等分”为 ｍ个组,要将选取出每一个组的组合数的乘积除以P(m,m)。

希望这篇博文对您有所帮助！！