[学习笔记] Splay Tree 从入门到放弃

前几天由于出行计划没有更博QwQ

(其实是因为调试死活调不出来了TAT我好菜啊)

伸展树

伸展树（英语：Splay Tree）是一种二叉查找树，它能在O(log n)内完成插入、查找和删除操作。它是由丹尼尔·斯立特（Daniel Sleator）和罗伯特·塔扬在1985年发明的^[1]。

在伸展树上的一般操作都基于伸展操作：假设想要对一个二叉查找树执行一系列的查找操作，为了使整个查找时间更小，被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法， 在每次查找之后对树进行调整，把被查找的条目搬移到离树根近一些的地方。伸展树应运而生。伸展树是一种自调整形式的二叉查找树，它会沿着从某个节点到树根之间的路径，通过一系列的旋转把这个节点搬移到树根去。

它的优势在于不需要记录用于平衡树的冗余信息。

优点

• 可靠的性能——它的平均效率不输于其他平衡树^[2]。
• 存储所需的内存少——伸展树无需记录额外的什么值来维护树的信息，相对于其他平衡树，内存占用要小。

缺点

伸展树最显著的缺点是它有可能会变成一条链。这种情况可能发生在以非降顺序访问n个元素之后。然而均摊的最坏情况是对数级的——O(log n)

以上摘自中文Wikipedia

永远不要用单旋代替双旋...单旋那叫Spaly,Splay中的势能分析在单旋时会失效,复杂度不对的...(警告某整天单旋的ryf)

Rotate操作:

在离散数学中，树旋转（英语：Tree rotation）是在二叉树中的一种子树调整操作, 每一次旋转并不影响对该二叉树进行中序遍历的结果. 树旋转通常应用于需要调整树的局部平衡性的场合。

然后上几张图来作一下左旋/右旋的说明:

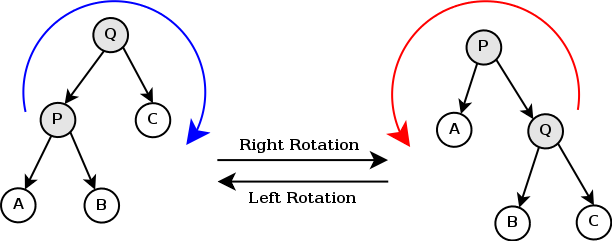
(第一张是动图不知道cnblogs能不能很好地滋磁GIF)

我们可以将左旋理解为将根旋转为右子节点的左子树,右旋为将根旋转为左子节点的右子树(往哪旋根就变成哪边的子树)

附C++袋马实现(左右合并,k=0为左旋,k=1为右旋)

#define lch chd[0]
#define rch chd[1]
#define kch chd[k]
#define xch chd[k^1]

void Rotate(Node* root,int k){
    Node* tmp=root->xch;
    if(root->prt==NULL)
        this->root=tmp;
    else if(root->prt->lch==root)
        root->prt->lch=tmp;
    else
        root->prt->rch=tmp;
    tmp->prt=root->prt;
    root->xch=tmp->kch;
    if(root->xch!=NULL)
        root->xch->prt=root;
    tmp->kch=root;
    root->prt=tmp;
}

Rotate

注:Node的定义:

struct Node{
    int k;
    Node* prt;
    Node* chd[];
    Node(const int& key){
        this->k=key;
        this->prt=NULL;
        this->lch=NULL;
        this->rch=NULL;
    }
    inline int size(){
        return this==NULL?:this->s;
    }
    inline int key(){
        return this==NULL?:this->k;
    }
    inline int Pos(){
        return this==this->prt->lch;
    }
};

Node

这样定义可以直接使用new与空指针NULL而且不必在每次都判空

还可以防止delete野指针造成RE

然后是在前面我为了方便而使用的宏定义:

 #define lch chd[0]
 #define rch chd[1]
 #define kch chd[k]
 #define xch chd[k^1]

Macro Definition

如果要维护子树大小还要记得旋转之后先维护原根(代码中的root)再维护新根(代码中的tmp)

Splay操作:

Splay(伸展)操作是Splay Tree的核心,作用是将一个指定的结点旋转到根的位置.

这时可分三种情况:

I.要伸展的结点的父节点就是根

这时直接一次单旋解决(Zig Step)

II.要伸展的结点的父节点不是根且要伸展的结点/该结点的父节点/该节点的祖父结点成一条直线

这时要先旋转祖父结点再旋转父节点且旋转方向相同(Zig-zig Step)

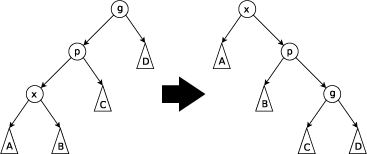
III.要伸展的结点的父节点不是根且要伸展的结点/该结点的父结点/该结点的祖父结点不在一条直线上

这时要先旋转父节点再反向旋转祖父结点(Zig-zag Step).需要注意的是旋转父节点后要伸展的结点的祖父结点变成了父结点.

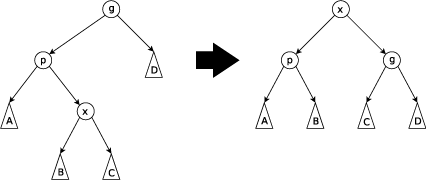
重复上面的情况直至要伸展的结点伸展至根.

实际应用时伸展函数有时候会有两个参数:要伸展的结点指针和根的父节点指针.这样可以控制结点不一定要伸展到整棵树的根而是一个子树的根.后面Insert和Delete操作中会用到.

然后是代码实现.这里将三种情况进行了适当合并,感性理解一下就好

 void Splay(Node* root,Node* prt=NULL){
     while(root->prt!=prt){
         int k=root->Pos();
         if(root->prt->prt==prt){
             this->Rotate(root->prt,k);
         }
         else{
             int d=root->prt->Pos();
             this->Rotate(k==d?root->prt->prt:root->prt,k);
             this->Rotate(root->prt,d);
         }
     }
 }

Splay

Insert操作:

这个操作有多种写法,对于最朴素的Splay可以先按照普通二叉树的方法插入结点,然后将插入的结点伸展到根.

如果题目要求需要维护子树大小来求第K大/小的值与某数的排名的话可以用双参Splay操作与K大/排名操作配合进行,先查找该值前驱伸展到根,然后查找该值后继伸展到根的右子树,然后直接将右子树的左儿子上新建一个结点.

第一种写法的代码是我从Wikipedia上摘录的,其中将模板部分替换为了int并将下划线命名规则改为大驼峰:

 void Insert( const int &key ) {
     Node *z = root;
     Node *p = ;

     while( z ) {
         p = z;
         if( key<z->key ) z = z->lch;
         else z = z->rch;
     }

     z = new Node( key );
     z->prt = p;

     if( !p ) root = z;
     else if( z->key<p->key ) p->lch = z;
     else p->rch = z;

     Splay( z );
 }

Insert:写法1

第二种写法的代码如下:

 void Insert(const int& key){
     int pos=this->Rank(key)-;
     this->Splay(this->Kth(pos));
     this->Splay(this->Kth(pos+),this->root);
     Node* tmp=new Node(key);
     this->root->rch->lch=tmp;
     tmp->prt=this->root->rch;
     this->root->rch->Maintain();
     this->root->Maintain();
 }

Insert: 写法2

注:Maintain()函数的作用为维护子树大小信息,Kth()为求K大函数,Rank()为求排名函数,定义见后续.

Delete操作:

Delete操作同样有多种写法,首先对于无附加信息的普通Splay:

首先查找到要删除的结点,然后伸展到根,并从它的右子树中查找值最小的结点并用它把待删除的结点替换掉.注意维护这两个结点周边结点的指针信息.代码如下,摘自Wikipedia:

 Node* Find( const T &key ) {
     Node *z = root;
     while( z ) {
         if(key<z->key())
             z=z->lch;
         else if(z->key<key)
             z=z->rch;
         else return z;
     }
     return NULL;
 }
 void Delete( const int &key ) {
     Node *z = Find( key );
     if( !z ) return;

     Splay( z );

     if( !z->lch ) Replace( z, z->rch );
     else if( !z->rch ) Replace( z, z->lch );
     else {
         Node *y = SubtreeMinimum( z->rch );
         if( y->prt != z ) {
             Replace( y, y->rch );
             y->rch = z->rch;
             y->rch->prt = y;
         }
         Replace( z, y );
         y->lch = z->lch;
         y->lch->prt = y;
     }

     delete z;
 }
 Node* subtreeMinimum( Node *u ) {
     while( u->lch ) u = u->lch;
     return u;
 }

Delete:写法1

注:Wikipedia中使用了两个辅助函数,一个是Find()用于查找,一个是SubtreeMinimum()用于查找子树最小值.这两个函数也摘录在上面的代码中了.

对于维护了子树大小附加信息的Splay则与Insert类似,不同的是一个是新建结点一个是切断连接并删除罢了

代码如下:

 void Delete(const int& key){
     int pos=this->Rank(key);
     this->Splay(this->Kth(pos-));
     this->Splay(this->Kth(pos+),root);
     delete this->root->rch->lch;
     this->root->rch->lch=NULL;
     this->root->rch->Maintain();
     this->root->Maintain();
 }

Delete:写法2

以上即为伸展树的几种基本操作.如果我们维护了子树大小的话还可以计算第K大/小的值与某数的排名,代码如下,具体原理不再详述.

 int Rank(const int& key){
     Node* root=this->root;
     int rank=;
     while(root!=NULL){
         if(root->key()<key){
             rank+=root->lch->size()+;
             root=root->rch;
         }
         else
             root=root->lch;
     }
     return rank;
 }

 void Insert(const int& key){
     int pos=this->Rank(key)-;
     this->Splay(this->Kth(pos));
     this->Splay(this->Kth(pos+),this->root);
     Node* tmp=new Node(key);
     this->root->rch->lch=tmp;
     tmp->prt=this->root->rch;
     this->root->rch->Maintain();
     this->root->Maintain();
 }

Kth/Rank

通过这两个函数还可求某数的前驱与后继的值,代码如下:

 inline int Predecessor(const int& key){
     return this->Kth(this->Rank(key)-)->key();
 }

 inline int Successor(const int& key){
     return this->Kth(this->Rank(key+))->key();
 }

Predecessor/Successor

对于Insert/Delete操作的第二种写法需要在进行所有操作前新建两个结点,值分别为INF与-INF来保证不会访问空指针

最后附上封装好的完整代码,维护了子树大小,可作为"普通平衡树"的模板.

 #define lch chd[0]
 #define rch chd[1]
 #define kch chd[k]
 #define xch chd[k^1]

 const int INF=0x7FFFFFFF;

 class SplayTree{
 private:
     struct Node{
         int k;
         int s;
         Node* prt;
         Node* chd[];
         Node(const int& key){
             this->k=key;
             this->s=;
             this->prt=NULL;
             this->lch=NULL;
             this->rch=NULL;
         }
         inline int size(){
             return this==NULL?:this->s;
         }
         inline int key(){
             return this==NULL?:this->k;
         }
         inline void Maintain(){
             if(this!=NULL)
                 this->s=this->lch->size()+this->rch->size()+;
         }
         inline int Pos(){
             return this==this->prt->lch;
         }
     }*root;

     void Rotate(Node* root,int k){
         Node* tmp=root->xch;
         if(root->prt==NULL)
             this->root=tmp;
         else if(root->prt->lch==root)
             root->prt->lch=tmp;
         else
             root->prt->rch=tmp;
         tmp->prt=root->prt;
         root->xch=tmp->kch;
         if(root->xch!=NULL)
             root->xch->prt=root;
         tmp->kch=root;
         root->prt=tmp;
         root->Maintain();
         tmp->Maintain();
     }

     void Splay(Node* root,Node* prt=NULL){
         while(root->prt!=prt){
             int k=root->Pos();
             if(root->prt->prt==prt){
                 this->Rotate(root->prt,k);
             }
             else{
                 int d=root->prt->Pos();
                 this->Rotate(k==d?root->prt->prt:root->prt,k);
                 this->Rotate(root->prt,d);
             }
         }
     }
 public:
     Node* Kth(int pos){
         Node* root=this->root;
         while(root!=NULL){
             int k=root->lch->size()+;
             if(pos<k)
                 root=root->lch;
             else if(pos==k)
                 return root;
             else{
                 pos-=k;
                 root=root->rch;
             }
         }
         return NULL;
     }

     int Rank(const int& key){
         Node* root=this->root;
         int rank=;
         while(root!=NULL){
             if(root->key()<key){
                 rank+=root->lch->size()+;
                 root=root->rch;
             }
             else
                 root=root->lch;
         }
         return rank;
     }

     void Insert(const int& key){
         int pos=this->Rank(key)-;
         this->Splay(this->Kth(pos));
         this->Splay(this->Kth(pos+),this->root);
         Node* tmp=new Node(key);
         this->root->rch->lch=tmp;
         tmp->prt=this->root->rch;
         this->root->rch->Maintain();
         this->root->Maintain();
     }

     void Delete(const int& key){
         int pos=this->Rank(key);
         this->Splay(this->Kth(pos-));
         this->Splay(this->Kth(pos+),root);
         delete this->root->rch->lch;
         this->root->rch->lch=NULL;
         this->root->rch->Maintain();
         this->root->Maintain();
     }

     inline int Predecessor(const int& key){
         return this->Kth(this->Rank(key)-)->key();
     }

     inline int Successor(const int& key){
         return this->Kth(this->Rank(key+))->key();
     }

     SplayTree(){
         this->root=new Node(-INF);
         this->root->rch=new Node(INF);
         this->root->rch->prt=this->root;
         this->root->rch->Maintain();
         this->root->Maintain();
     }
 };

Full Splay Tree

然后是图包时间QwQ