TensorFlow简易学习[2]:实现线性回归
上篇介绍了TensorFlow基本概念和基本操作,本文将利用TensorFlow举例实现线性回归模型过程。
线性回归算法
线性回归算法是机器学习中典型监督学习算法,不同于分类算法,线性回归的输出是整个实数空间R(故也可用线性回归做分类)。关于线性回归网络资料很多,算法具体推演不做叙述,这里简要概括基本点。
目标函数y(不考虑噪声形式):
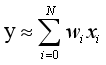
损失函数Loss:
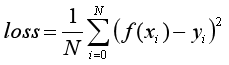
求解方法梯度下降:
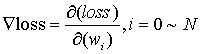
TensorFlow实现
代码
#!/usr/bin/pyton import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt x_data = np.random.rand(100).astype(np.float32)
y_data = x_data*0.1 + 0.3 Weights = tf.Variable(tf.random_uniform([1], -1.0, 1.0))
biases = tf.Variable(tf.zeros([1])) y = Weights*x_data + biases loss = tf.reduce_mean(tf.square(y-y_data))
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss) sess = tf.Session()
#initialize_local_variables no more support in new version
if int((tf.__version__).split('.')[1]) < 12 and int((tf.__version__).split('.')[0]) < 1:
init = tf.initialize_all_variables()
else:
init = tf.global_variables_initializer() sess.run(init)
plt.figure()
for step in range(201):
sess.run(train) plt.scatter(x_data, sess.run(y))
plt.plot(x_data, sess.run(y), color = 'red')
plt.show()
sess.close()
结果
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAoAAAAHZCAYAAAAWpIqBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAIABJREFUeJzt3Xl4VOX99/HPZIeUBCHNIkQTFosRENlCiEqlofigKOXnT4pVKYqAClLTKokiJNWKWJTUgvKT5+cGAtalKjZNq0ELkWAqywMxogjBBZKwlSSAJDBznj9iBoaZCZmQTGbmvF/Xletq7rnncM8pOh+/55zvbTEMwxAAAABMI6i9FwAAAADvIgACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEwmpL0X4M9sNpv27dunTp06yWKxtPdyAABAMxiGodraWl144YUKCjJnLYwAeB727dunxMTE9l4GAABogW+//Vbdu3dv72W0CwLgeejUqZOkhr9AUVFR7bwaAADQHDU1NUpMTLR/j5sRAfA8NF72jYqKIgACAOBnzHz7ljkvfAMAAJgYARAAAMBkCIAAAAAmQwAEAAAwGQIgAACAyRAAAQAATIYACAAAYDIEQAAAAJMhAAIAAJgMARAAAMBkCIAAAAAmQwAEAAAwGQIgAACAyRAAAQAATIYACAAAYDIEQAAAAJMhAAIAAJgMARAAAMBkCIAAAAAmQwAEAAAwGQIgAACAyRAAAQAATIYACAAAYDIEQAAAAJMhAAIAAJgMARAAAMBk/CYALlmyRElJSYqIiFBqaqpKSkqa9b6PP/5YISEhGjBggNNrr7/+uvr06aOIiAj169dP+fn5rb1sAAAAn+MXAfC1115TZmam5s2bp82bN+vyyy/X6NGjtX///ibfd+TIEd1+++362c9+5vTahg0bNHHiRN15553asmWLxo0bp3Hjxqm0tLStPgYAAIBPsBiGYbT3Is4lNTVVQ4YM0eLFiyVJNptNiYmJmjlzprKysty+75e//KV69+6t4OBgvf3229q6dav9tQkTJujYsWN677337GPDhg3TgAEDtHTp0matq6amRtHR0aqurlZUVFQLPx0AAPAmvr/9oAJYX1+vTZs2KSMjwz4WFBSkjIwMFRcXu33fiy++qN27d2vevHkuXy8uLnY4piSNHj26yWMCAAAEgpD2XsC5HDx4UFarVXFxcQ7jcXFx2rFjh8v37Ny5U1lZWVq/fr1CQlx/xMrKSpfHrKysdLuWuro61dXV2X+vqalp7scAAADwGT5fAfSU1WrVLbfcotzcXF1yySWteuz58+crOjra/pOYmNiqxwcAAPAGn68AxsTEKDg4WFVVVQ7jVVVVio+Pd5pfW1urTz/9VFu2bNGMGTMkNdwzaBiGQkJC9M9//lMjR45UfHx8s4/ZKDs7W5mZmfbfa2pqCIEAALQCq83Qxt2HVLzrkCRDaT1iNKxnVwUHWdp7aQHJ5wNgWFiYBg0apMLCQo0bN05SQ6ArLCy0B7wzRUVFafv27Q5jzz77rNauXas33nhDycnJkqS0tDQVFhbqN7/5jX3e+++/r7S0NLdrCQ8PV3h4eGt8LAAA8IP8bRV68M1tOlp3yj62+MNd6twxVE+M76dr+ya04+oCk88HQEnKzMzUpEmTNHjwYA0dOlR5eXk6duyYJk+eLKmhMrd371698sorCgoKUt++fR3eHxsbq4iICIfxWbNmacSIEXrqqad03XXXafXq1fr000/1/PPPe/WzAQBgZvPzy/Q/68pdvnbk+ElNX7FZS28dSAhsZX4RACdMmKADBw5o7ty5qqys1IABA1RQUGB/iKOiokLffPONR8ccPny4Vq5cqTlz5uihhx5S79699fbbbzuFRwAA0Dbyt+1zCn+h1pM6GRQiWU5f+s159zONSonncnAr8os+gL6KPkIAALSM1WZoyB/e1+FjJyVJvQ98rfdfuFeS9HrfDD1w3W8c5q+6a5jSenZtlT+b728/qQACAIDAUlJ+2B7+9iy43uG1hNoDTvP3157wyrrMIuDawAAAAN+3v/aEpn7yplP4k6Rbf/kHp7HYThHeWJZpUAEEAADeZbPpxiu668azhn990zx91HOI0/T4qHANTe7inbWZBAEQAAC0uvpTNr28oVz/3vMfRYYFa/zA7hreK0bBI6+R/vUvp/lJs99ze6ycGy7jAZBWRgAEAACtan5+mZ5fV64znzL9sHiHtj5zi9PcK6e/oO+iY10ep2NYsJ6++XJawLQBAiAAAGg1rvr6ubrPT926Sd99pzmlFcpdU6aK6tMPeUSGB2vKlT103896U/lrIwRAAADQKupP2fT8GeHv2i8+1tK35zvNu/r3+frw4WsVLOnavgkalRKvkvLD2l97QrGdIjQ0uQvBr40RAAEAQKtYXrzHftnXVdXvxUFjlZsxTTpmU0n5YXtfv+AgS6v1+EPzEAABAECr+Prwca19fqp6/Gef02tnP+RBX7/2RR9AAABw/mw2/X5cP6fw92bfkS6f8KWvX/uiAggAAJrNajOc79cLdl1PctfaJSE6gr5+7YwACAAAmtQY+t4vq9TbW/fp8LF6SVL36ioVLb3Taf6tNz+qouQr3B5v3tgUHvJoZwRAAADgVoGLNi2Sm9YukmQYuiy/TB+f1QdQamjv8tR/09fPF1gMwzj7/x80U01NjaKjo1VdXa2oqKj2Xg4AAK2qoLRCd6/Y7BDkppS8pTkfvuA09+eP/FV/z7nRXtlzuxOID1T++P6mAggAAFyw2gzlrilzCH/uqn5Js9+T6uXQ2iUsJEh3Xd1Td13thcXCYwRAAADgpKT8sP2yb5PB7wy0dvEftIEBAABO9teekAzDZfjbmtCb1i5+jgogAABwcuMV3XWji3FXwc8iKZ7WLn6FCiAAADht1y7J4vygxpyf3+M2/Em0dvE3VAABAEADF8FPkpJnv+fU0qVRfHSE5o1NobWLnyEAAgBgdk8+Kc2e7Tz+7bcqOBKs+LP6AHaJDNUvBnRTRkp8w04gVP78DgEQAAAzc1P10w9tgq/tLo1KiXfe/o3Q59cIgAAAmFFYmHTypPO4zeYUCoODLPb+fggMBEAAAAJU4x6+DpU7i6QgF8+AhoZK9fVeXyPaBwEQAIAA5GoP36b274W50AYGAIAAYbUZKt51SL9f85mmr9hsD3/xNQddh78nniD8mRQVQAAAAoCrip/kvupntdp4kMPECIAAAPgxq83Q4rU7teiDnQ7j0z55Q9kfveQ0/+qpy/TNBQlaVX6YBztMjAAIAICfKiitUM67ZaqsaV7V78ydPPbXnnA5B+ZAAAQAwA/lb6vQPSs3O4y5DX4PrnFq7RLbKaLN1gbfRwAEAMCPWG2G/lz4pf5U+JXDeHOqflLD3r3x0Q0tYWBeBEAAAPxEQWmFst7ariPHTzdwbm7wkxrCnyTNG5vCAyAmRxsYAAB8nNVm6E8f7NT0FZvt4a/7kUqX4e/tlBEuw5/UUPl77taBurZvQpuuF76PCiAAAD6s4UGPz1RZU2cf86TqJ0l3picpIyWePXxhRwAEAMBHFZRW6O4Vm9XYqvmxfyzRrVv/7jRv/K/+qM3dL3Uaj48KV84Nl1HxgxMCIAAAPuLMvXtjIsOV826ZPfx5WvW7P+MSzRjZi4ofXCIAAgDgAzzdyaPnA+/IGhTsNB5kkRZPHKgx/an6wT0CIAAA7Sx/2z7ds3KL07inVT9JWjzxCsIfzokACABAO8rfVqEZqxzDX0uCX+eOoXpifD/u90OzEAABAPCyxnv93i+r1Asf77GPx9cc1Mbnfu003yaLesxe4/JYnTuEanJ6Mvf7wSMEQAAAvMRqM7R47U69+PEeHfn+pMNrLan63Z/RWzNG9ib4wWMEQAAAvMDVLh6S9EjhMt356TtO82fc8KDeu/Rql8dKiI7QvLEpXO5FixEAAQBoY/nbKnTPys1O482t+sVHheupmwfo4NE6xXaKoKEzzhsBEACANpS/bV+zH/L4yW/fUl1ImNN4zg2XKb1XTJusD+ZEAAQAoI0UlFY4tXfx5F6/hp5+V3CpF62OAAgAQBuw2gzlrimz/96ynn40dEbbIAACANBKztzK7WBtnSqqT+jHRw/r30tudznfXfjjIQ+0taD2XkBzLVmyRElJSYqIiFBqaqpKSkrczi0qKlJ6erq6du2qDh06qE+fPlq0aJHTvLy8PP3kJz9Rhw4dlJiYqPvvv18nTpxwcUQAAJpWUFqhKxes1cRlGzVr9VY9+rfPtWfB9S7DX9Ls91yGvzvTk7TqrmEqmj2S8Ic25RcVwNdee02ZmZlaunSpUlNTlZeXp9GjR+uLL75QbGys0/zIyEjNmDFD/fv3V2RkpIqKijRt2jRFRkZq6tSpkqSVK1cqKytLL7zwgoYPH64vv/xSkydPlsVi0dNPP+3tjwgA8FMNvf2+0qIPvrSPPfaPJbp169+d5i686lYtHv5Lp3F28YC3WQzDMNp7EeeSmpqqIUOGaPHixZIkm82mxMREzZw5U1lZWc06xvjx4xUZGanly5dLkmbMmKHPP/9chYWF9jm//e1v9cknn6ioqKhZx6ypqVF0dLSqq6sVFRXl4acCAPi7gtIK5bz7mSpr6uxjntzrZ5E062e9NfNnNHP2Jr6//eAScH19vTZt2qSMjAz7WFBQkDIyMlRcXNysY2zZskUbNmzQiBEj7GPDhw/Xpk2b7JeSd+/erfz8fI0ZM6Z1PwAAICAVlFbo7hWb7eFvz4LrXYa//rNWu73Xb8ktV+g3oy4h/MHrfP4S8MGDB2W1WhUXF+cwHhcXpx07djT53u7du+vAgQM6deqUcnJyNGXKFPtrt9xyiw4ePKgrr7xShmHo1KlTmj59uh566CG3x6urq1Nd3en/yqupqWnhpwIA+LPGJ3wbL6F5+oQvD3mgvfl8ADwf69ev19GjR7Vx40ZlZWWpV69emjhxoiTpo48+0uOPP65nn31Wqamp+uqrrzRr1iw9+uijeuSRR1web/78+crNzfXmRwAA+KCS8sOqqD7hUfB75LpLFdMpnJ084BN8/h7A+vp6dezYUW+88YbGjRtnH580aZKOHDmid95x3j/Rlccee0zLly/XF198IUm66qqrlJqaqoULF9rnrFixQlOnTtXRo0cVFOR8ddxVBTAxMdHU9xAAgBnl/6tUY37az+VrZ4c/i6T46AgVzR5J6PMR3APoBxXAsLAwDRo0SIWFhfYAaLPZVFhYqBkzZjT7ODabzSG8HT9+XCEhjh8/ODhYkuQuE4eHhys8PNzTjwAA8DNn9vNzqthZLHJ1t3hTDZ3njU0h/MGn+HwAlKTMzExNmjRJgwcP1tChQ5WXl6djx45p8uTJkqTs7Gzt3btXr7zyiqSGnoEXXXSR+vTpI0lat26dFi5cqPvuu89+zLFjx+rpp5/WgAED7JeAH3nkEY0dO9YeBAEA5lNQWqHcNWWqqD7dFzYhOkKv7nxTPV58zmn+ystH66FrZ7o8Fvf6wVf5RQCcMGGCDhw4oLlz56qyslIDBgxQQUGB/cGQiooKffPNN/b5NptN2dnZKi8vV0hIiHr27KkFCxZo2rRp9jlz5syRxWLRnDlztHfvXv34xz/W2LFj9Yc//MHrnw8A4Bsan+w9+zpQ8UMZLucnN1H1uz+jt2aMpL0LfJPP3wPoy7iHAAACg9VmaMNXBzX91U06Vme1j7t7yEP79kkJCW6rhVT9fBvf335SAQQAoK0UlFYo663tOnL8pMO4u/BX/NVBpSV0lSRd2zdBo1Li3d8vCPgoAiAAwHSsNkMbdx3Sik/26O+lVQ6vnau1y59qHfeMDw6yKK1n17ZZKNBGCIAAAFNxV/HrWP+9yhb9t8v3nPmEb2yniDZdH+ANBEAAgGkUlFZo+orNTuPNaejc2M9vaHKXtloe4DU+vxcwAACtwWozlPPuZw5j9254zWX4K7r4cpd9/ejnh0BBBRAAYAol5YdVWXN6QwBPtnHrEhmqx3/Rjyd7ETAIgAAAU9j/w8Mb7oLfiKnP6+sLLnQa79IxVBuzMxQWwkUzBA4CIADAFGI7RXhU9Wv0+Ph+hD8EHAIgACDwWSxKczHcVPDr3DFUT4znsi8CEwEQABC46uqkCNdtW9yFv//TN063piZpWM+uPPCBgEUABAAEJovr8FawfZ+y3toundUH8IKOoZpPxQ8mQQAEAASWZ56RZs1yHr/oIunrr3WtpFEp8dq465CKdx+U1LCTx7AeVPxgHgRAAEDgcFP1k2E4/BocZFF67xil947xwqIA38NjTQAA/2exuA5/n37qFP4AUAEEAPi7Zlb9AJxGAAQA+CeCH9BiXAIGAPgXq5XwB5wnKoAAAP9B8ANaBRVAAIDvW7nSdfgLCiL8AS1ABRAA4BOsNkMl5Ye1v/aEYjtFaGhyl4a+fFT9gFZHAAQAtLv8bfs0551SHT52eneOPQuudz157Vrpmmu8tDIgMBEAAQDtxmoz9JvVm7VmW6XDuNvwR9UPaBUEQABAuygorVDWW9t15Pi5q37WU1YFB3PbOtBa+KcJAOB1BaUVunvF5tPhzzDchr+k2e+pZM9/vLg6IPBRAQQAeJXVZih3TZkaL+Y2Ffwa7a894YWVAeZBBRAA4FUl5YdVUX1CP/+yuFnhT5JiO0V4Y2mAaVABBAB41f7aE80OfpLUJTJUQ5O7tPWyAFMhAAIA2oTLvn7BQbrRxdxZ1/9W71zmurXLYzf2begHCKDVEAABAK2uoLRCuWvKVFF9+t49T6p+jaZdnawx/S9s9fUBZkcABAC0isaK3wdllfrfj/fYx90Fvx4PvivD4vpW9B+Fh+jJ/+qvMf0T2mKpgOkRAAEA58VqM7R47Vd68eNyHfn+pMNrbvv6WW16tqzSqUrYuWOoJg9P1oyRvbjsC7QhAiAAoMVcNXOWzn25d1X5YV3bN0GjUuJd7/8LoE0RAAEALVJQWqHpKzY7jA3fs1UrX5vjcr6rvn7BQRal9ezadosE4BIBEADgscZmzmfy5CEP+voB7YsACADwWGMzZ8l98Hvsmjv0f4eOdxizSIqPjqCvH9DOCIAAgHM6u6dfZfX3kjyr+jXe2TdvbAr3+QHtjAAIAGiSu55+v3Axt/fv/qqTwaEujxMfHaF5Y1N0bV9auwDtjQAIAHCpsb3Log++dBj3tKHzHelJGpUSzxO+gA8hAAIAnBSUVijn3c9UWVNnH/M0+F3QMVTzx/ej4gf4IAIgAMCuoeq3U4s+2Gkf61v5ld57+Tcu5yfNfk9dIkN1+NjpPoCdO4RqcnqSZozsTcUP8FEEQACA/XLvCx+Xq/qM3TyaU/V75PrLFB8VQTNnwI8QAAHA5Fzt5rHryRsUbNic5i4dOl5PXHOHw1h8VATNnAE/QwAEABNztZtHc+/1o6cf4L8IgABgUmfv5uEu+F16/xv6Psz1zh309AP8EwEQAEyqObt5uHvCN4GefoBfIwACgEntrz3hcfCTpPszevOEL+DnCIAAEMDqT9m0vHiPvj58XBd36ajb0pIUFhIk7dihG6+41OV73IW/+Khw5dxwGVU/IAAQAAEgQM3PL9Oy9eWyGafH/pD/uXY/0ZKq3yWaMbIXVT8gQAS19wKaa8mSJUpKSlJERIRSU1NVUlLidm5RUZHS09PVtWtXdejQQX369NGiRYuc5h05ckT33nuvEhISFB4erksuuUT5+flt+TEAwCvm55fpf9Y5hr9PltzuMvy93ytVyU3s5rH01oGalcElXyCQ+EUF8LXXXlNmZqaWLl2q1NRU5eXlafTo0friiy8UGxvrND8yMlIzZsxQ//79FRkZqaKiIk2bNk2RkZGaOnWqJKm+vl6jRo1SbGys3njjDXXr1k1ff/21Onfu7O2PBwCtqv6UTcvWlzuMubvXT4Yha2mF4teU2R8IkdjNAwh0FsMwjHNPa1+pqakaMmSIFi9eLEmy2WxKTEzUzJkzlZWV1axjjB8/XpGRkVq+fLkkaenSpfrjH/+oHTt2KDQ0tEXrqqmpUXR0tKqrqxUVFdWiYwBAa/vf9bv16N8+l+Q++A2c+aru/e9huvOqHpIaWsKUlB9mNw+YAt/ffnAJuL6+Xps2bVJGRoZ9LCgoSBkZGSouLm7WMbZs2aINGzZoxIgR9rF3331XaWlpuvfeexUXF6e+ffvq8ccfl9VqdXucuro61dTUOPwAgK/5+vBxSU23djncMdo+T5KCgyxK69lVNw7oprSeXQl/QIDz+UvABw8elNVqVVxcnMN4XFycduzY0eR7u3fvrgMHDujUqVPKycnRlClT7K/t3r1ba9eu1a9+9Svl5+frq6++0j333KOTJ09q3rx5Lo83f/585ebmnv+HAoA29Ptx/fR7F+NnP+RxcZeO3lkQAJ/j8xXA87F+/Xp9+umnWrp0qfLy8rRq1Sr7azabTbGxsXr++ec1aNAgTZgwQQ8//LCWLl3q9njZ2dmqrq62/3z77bfe+BgA0DzffitZXFfuzg5/QRbptrQkLywKgC/y+QpgTEyMgoODVVVV5TBeVVWl+Pj4Jt+bnJwsSerXr5+qqqqUk5OjiRMnSpISEhIUGhqq4OBg+/xLL71UlZWVqq+vV1hYmNPxwsPDFR4efr4fCQBazO29es0Mfo3uuiq5oR8gAFPy+X/6w8LCNGjQIBUWFtrHbDabCgsLlZaW1uzj2Gw21dXV2X9PT0/XV199JZvNZh/78ssvlZCQ4DL8AUB7Kyit0JUL1mriso2atXqrJi7bqK8SL3Ed/i69VPP/9pnOvpUvyCJNuzpZ2WNSvLNoAD7J5yuAkpSZmalJkyZp8ODBGjp0qPLy8nTs2DFNnjxZUsOl2b179+qVV16R1NAz8KKLLlKfPn0kSevWrdPChQt133332Y959913a/HixZo1a5ZmzpypnTt36vHHH3eYAwC+oqC0Qnev2Kwz2zY01dpFkrIl/fbnfVzvBALA1PwiAE6YMEEHDhzQ3LlzVVlZqQEDBqigoMD+YEhFRYW++eYb+3ybzabs7GyVl5crJCREPXv21IIFCzRt2jT7nMTERP3jH//Q/fffr/79+6tbt26aNWuWZs+e7fXPBwDuWG2GNu4+pKw3t9vDn7vgZ/1ql4J79nAYCwsJsrd6AYBGftEH0FfRRwhAW2gMfSs2fq11Xx7QsfrT7amaau2y6q5hSuvZ1VvLBPwW399+UgEEALMoKK1Q1lvbdeT4SYfxpoJfo/21J1zOAYCzEQABwEcUlFZo+orNDmOdv6/R1mducTn/7Cd8YztFtNnaAAQWAiAA+ACrzVDOu2UOY82p+kmSRVJ8dENLGABoDgIgAPiAkvLDqqxpuIT78l/makT5ZpfzXIU/SZo3NoXt2wA0GwEQAHxA4/17za36NYqPjtC8sSm6tm9Cm60NQOAhAAKAD7jxiu660cX4mF8/o7I45zYunTuGasnEgRrWsyuVPwAeIwACgJe01jZukvTE+H5K7x3TVksFEOAIgADgBQWlFcpdU6aK6tOtWjy93Cs1VP6eGN+PS74AzgsBEADa2NnbuHWoP6HPF93keu72fersog9gx7BgTbu6p2aM7MUlXwDnjQAIAG3IajOUu6bs3Nu4WW0KDrLoWkmjUuK1cfchFe86JMlQWo8Y7vUD0KoIgADQhkrKD6ui+oR+/8/ndPuWv7mckzT7Pa0qP2zfxi04yKL0XjFK78U9fgDaBgEQAFqJq4c89teeYBs3AD6HAAgA58lqM7R47U69+PEeHfn+9L17exZc77K1y3/f8oT+ndjXYYxt3AB4EwEQAFqoIfh9pefX7dKxeqvDa2zjBsCXEQABoAXyt+3Tg29u09G65gW/ZBetXdjGDUB7CWrvBQCAv5mfX6Z7Vm5xCH8h1lNNVv1+k3GJ4qMdL/PGR0fouVsH0tMPgNdRAQSAZrLaDP3pgy/1P+vKHcabc7k3KaajimaPdL0TCAB4GQEQAJqhoLRCWWc1aJ6+8Q1l/esll/PPvtcvtlOEgoMs9lYvANCeCIAAcA4FpRWavmKzw5gn27gl8JAHAB9DAASAJlhthnLeLbP/7i743TV+jt7vPczlazzkAcDXEAABoAkl5YdVWdPQpNmTqp8kde4YqifG9+MhDwA+hwAIAD84n508ztQxLFjTru6pGSN7UfkD4JMIgACghvv8cteUqaL69JZsCVHhKn54lMv57sLf2P7xyvvlQIIfAJ9GAARgao27eSz64EuHcU+rfpL054lXaOzlF7bq+gCgLRAAAZhWQWmFct79TJU1dfax/9peqKfyF7mc31T4e/aWKzSmP+EPgH8gAAIwpYLSCt29YrOMM8aaqvrdn9FbnTfscegDKPGgBwD/RAAEYDpWm6HcNWX28Ocu+D3wf2bp9f4N9wAmxURq05xR2rj7kIp3HZJkKK1HjIb17Mr9fgD8DgEQgCmc+YTvwdo6+8Mezb3Xr3Enj/ReMUrvFdPm6wWAtkQABBDwXD3h6y74JT/4rgxLkP13i6R4dvIAEGAIgAACmqf3+rnCTh4AAg0BEEDAau69fu6CX0J0hOaNTeEBDwABhwAIIGCVlB9WRfUJ/XTXv/XSG7ku57gLf/dn9NaMkb2p/AEISARAAAGrJdu4UfUDYAYEQACByWLRjS6GH//pZD2f+l8OY49cd6liOoXb9/+l6gcg0BEAAfi1M9u72APW81NZAAAgAElEQVRccJDLuWdX/Rqf8P11ejKhD4CpEAAB+K2z27u4u9zb+3dv61Sw47/uGuMeT/gCMCPX/5kMAD6usb3LucKfDEN/njRU8dERDsPx0RF67taB3OsHwJSoAALweWdf5h108QX29i7ugl/a4x+oaPZIBUu6tm+CRqXEO18qpvIHwKQIgAB8mqtdPLpEhuqinaUqXv5bl+9Jmv2eVH1CJeWHldazqyQpOMhi/98AYHYEQAA+K3/bPt2zcovT+Oa5o13OP/shj/21J1zOAwCzIwAC8En52yo0Y5Vj+Nv15A0KNmxOcxen3ayFV9/uNB7bKcJpDABAAATggwpKK3TPys0OY540dG5s7zI0uUtbLA8A/B4BEIBPady/t5G74Ncn8w2dCHWu8NHeBQDOjTYwAHxK4/69UtNVv8bw1yUyzOE12rsAwLlRAQTgUzzZvzchOkL/euAabfr6P7R3AQAPEAAB+I6yMt14xWUuX3J1r9+8sSkKCwmivQsAeIgACMCrXO7dG2SRLK6rdq6CX5BFWjzxCi7zAkAL+c09gEuWLFFSUpIiIiKUmpqqkpISt3OLioqUnp6url27qkOHDurTp48WLVrkdv7q1atlsVg0bty4tlg6gB8UlFboygVrNXHZRs1avVUTl23UgS5xLsPfXy+7Rskuwp8kLZ44UGP6X9jWywWAgOUXFcDXXntNmZmZWrp0qVJTU5WXl6fRo0friy++UGxsrNP8yMhIzZgxQ/3791dkZKSKioo0bdo0RUZGaurUqQ5z9+zZo9/97ne66qqrvPVxAFNq3LvXOGOsqf17O5RWKP6sHUASoiM0b2wKlT8AOE8WwzCMc09rX6mpqRoyZIgWL14sSbLZbEpMTNTMmTOVlZXVrGOMHz9ekZGRWr58uX3MarXq6quv1h133KH169fryJEjevvtt5u9rpqaGkVHR6u6ulpRUVGefSjABKw2Qxt3H9KGrw7qpQ17dKzeKsl98LMeOKjgmK4O72f/XgCtje9vP6gA1tfXa9OmTcrOzraPBQUFKSMjQ8XFxc06xpYtW7RhwwY99thjDuO///3vFRsbqzvvvFPr168/53Hq6upUV1dn/72mpqaZnwIwn4LSCmW9tV1Hjp90GG/qCd9V1VJazOkx9u8FgLbh8wHw4MGDslqtiouLcxiPi4vTjh07mnxv9+7ddeDAAZ06dUo5OTmaMmWK/bWioiL97//+r7Zu3drstcyfP1+5ubmefQDAhApKKzR9hec7ebB3LwB4h988BNIS69ev16effqqlS5cqLy9Pq1atkiTV1tbqtttu07JlyxQTE3OOo5yWnZ2t6upq+8+3337bVksH/JbVZijn3dM7eSTUHGh2Xz/27gUA7/D5CmBMTIyCg4NVVVXlMF5VVaX4+Pgm35ucnCxJ6tevn6qqqpSTk6OJEydq165d2rNnj8aOHWufa7M1bDAfEhKiL774Qj179nQ6Xnh4uMLDw8/3IwEBraT8sCprzr2Tx5nYuxcAvMvnK4BhYWEaNGiQCgsL7WM2m02FhYVKS0tr9nFsNpv9/r0+ffpo+/bt2rp1q/3nhhtu0DXXXKOtW7cqMTGx1T8HYBb7a0/ozeW/cxn+/pU80GX4k9i7FwC8yecrgJKUmZmpSZMmafDgwRo6dKjy8vJ07NgxTZ48WVLDpdm9e/fqlVdekdTQM/Ciiy5Snz59JEnr1q3TwoULdd9990mSIiIi1LdvX4c/o3PnzpLkNA7AMzde0d3luKuGzlJD5Y/WLgDgXX4RACdMmKADBw5o7ty5qqys1IABA1RQUGB/MKSiokLffPONfb7NZlN2drbKy8sVEhKinj17asGCBZo2bVp7fQQg8LnZyWPY3S+pMsr5XtvoiBA9e+sgDevRlcofAHiZX/QB9FX0EQJ+4ME2bo2W3jqQqh+AdsH3tx/cAwjAh1nc7OFrGCrYvk+dO4Y6vdS5YyjhDwDamV9cAgbgYw4dkty1UPrhosK1fRM0KiVeG3cfUvGuQ5IMpfWI0bCeXPIFgPZGAATgGTeXe+XibpLgIIvSe8UovVfz+20CANoel4ABOLHaDBXvOqR3tu5V8a5DstoMacIE1+GvRw+X4Q8A4LuoAAJwUFBaodw1ZaqoPr0tm7uGzgQ/APBPBEAAdgWlFbp7xWY1xjq3wW/HDuknP/HaugAArYsACEBSw2Xf3DVl5wx/VquNhzgAwM8RAAFIatjDt6L6xDn3711VflhpPbt6c2kAgFbGQyAAJEmH9h8+Z/iTGvb6BQD4NyqAACSLRa6in6udPGI7RbT9egAAbYoKIGBm99/f7G3cLJISoiM0NLmLFxYGAGhLVAABs3IT/JJdVP0aZ84bm8IDIAAQAKgAAgHKZTNnyf3+vZ98IhmGnrt1oOKjHS/zxkdH6Dn27wWAgEEFEAhArpo5J0RHqPihDNdvOKOhc+MeviXlh7W/9oRiOzVc9qXyBwCBgwAIBJizmzlLnu/kERxkodULAAQwLgEDAeTsZs6h1pNs4wYAcEIFEAggjc2cJfdVv6TZ72nVXcOU5s2FAQB8CgEQ8GNWm+Fwr15l9fe67+NVyix61eX8xtYuNHMGAHMjAAJ+pjH0vV9Wqbe37tPhY/X215qzk4dEM2cAMDsCIOBHCkorlPNumSprHCt47oLfr2/K0Uc9B9t/t6ihpQvNnAHA3AiAgJ8oKK3Q9BWbncabW/WjmTMAoBEBEPADVpuh3/7l/zmMnSv4dYkM1eFjJ+3j8dERmjc2hWbOAAACIOAPNnx1UMfqrZIki2FT+ZM3uJx3ZtXvkesvU3xUBM2cAQBOCICAH3hr83eSmn+5V5LioyJo5gwAcIkACPgQq83Qxt2HVLzrkCRDaT1iNKxnV/X7cI0WPT/P5Xtc3evHgx4AgKYQAAEfUVBaoay3tuvI8dP37S3+cJf2LLhed7iY76rq14gHPQAATSEAAu3MajO0eO1OLfpgp8O4u8u9d9+Ypb/3udLlawk86AEAaAYCINCO3tmyV1lvbdP3J20O457c69dobP945f1yIJU/AMA5EQCBdnLD4vXa9l2Nw5jb4PfgGsli0fX9E/S3bRUyznjNImnq1cnKHpPSdosFAAQUAiDQDqa8XOIY/gxDe54c63LumVW/USlxevrmAVpevEdfHz6ui7t01G1pSQoLCWrjFQMAAgkBEPCy7+ut+uDzA/bfPbncG9spQmEhQbrzqh5ttj4AQOCjbAB42eP5ZZKkYd9s87CvXzitXQAArYIKIOBlew4db9FDHjk3XMYDHgCAVkEABLwpKEjLDcNpeNb1v9U7l13j8i2dO4bqifH9aO0CAGg1BEDAWyyuq3fuqn4/T4nVpLRkDevZlcofAKBVEQCBtuYm+PV44B3ZgoJdvta/e5Sev31IW64KAGBiPAQCtCU34U+GoZ+5uaSbcemP9e6Mq9pwUQAAs6MCCJwHq81QSflh7a89odhOERqa3KXhcm0Twa/RstuH6Pt6qx7PL9OeQ8eV1LWjHhqTog5hrquCAAC0FgIg0EL52yo0551SHT5Wbx8bcfRbvbzkbtdvcPHwR4ewYD06rl9bLREAAJcIgEALzM8v0/+sK3cYc9faxVXwAwCgPXEPIOCh/G37HMJf0XN3uAx/trw8wh8AwCdRAQSaof6UTcuL92jPoeN6Y9O39vGmGjqvun6Y0ry0PgAAPEEABM5hfn6Zlq0vl+2MYp674HfJb/+q+pBQSdL+2hPeWB4AAB4jAAJN8ORev7MbOsd2imizdQEAcD4IgIAb9adsWrb+dPjzZP/erpFhGprcpc3WBgDA+SAAAmc4s6/fp3sOy2ZIyYf36sNl01zOd7eN26M39mX7NgCAzyIAAj8oKK1Q7poyVVSfvnfPk6pfo2lXJ2tMf9e7fAAA4Av8pg3MkiVLlJSUpIiICKWmpqqkpMTt3KKiIqWnp6tr167q0KGD+vTpo0WLFjnMWbZsma666ipdcMEFuuCCC5SRkdHkMRHYCkordPeKzfbw9/qKB12Gv8VpN7sNf10iQ/XsLVcoe0xKm64VAIDz5RcVwNdee02ZmZlaunSpUlNTlZeXp9GjR+uLL75QbGys0/zIyEjNmDFD/fv3V2RkpIqKijRt2jRFRkZq6tSpkqSPPvpIEydO1PDhwxUREaEFCxbo5z//uT777DN169bN2x8R7chqM5S7pkyND/l6UvULskh//K/+uvCCjqe3gQMAwMdZDMP3O9WmpqZqyJAhWrx4sSTJZrMpMTFRM2fOVFZWVrOOMX78eEVGRmr58uUuX7darbrgggu0ePFi3X777c06Zk1NjaKjo1VdXa2oqKjmfRi0u7P377UZhn71fz9xG/wu+81fdCy8o8vXpl2dTMUPAPwM399+UAGsr6/Xpk2blJ2dbR8LCgpSRkaGiouLm3WMLVu2aMOGDXrsscfczjl+/LhOnjypLl14cjNQWW2GFq/dqRc/3qMj35+0j3fuEOrxvX5BFumuqwh/AAD/5PMB8ODBg7JarYqLi3MYj4uL044dO5p8b/fu3XXgwAGdOnVKOTk5mjJlitu5s2fP1oUXXqiMjAy3c+rq6lRXV2f/vaamppmfAu3tva379Ls3/59OnLQ5jHsS/G4bdpEsFosu7tJRt6UlKSzEb26hBQDAgc8HwPOxfv16HT16VBs3blRWVpZ69eqliRMnOs174okntHr1an300UeKiHDfvHf+/PnKzc1tyyWjDdz1yr/1ftl+h7G42oP65Nlfu5x/dvizSIqPjlDODbR2AQAEBp8PgDExMQoODlZVVZXDeFVVleLj45t8b3JysiSpX79+qqqqUk5OjlMAXLhwoZ544gl98MEH6t+/f5PHy87OVmZmpv33mpoaJSYmevJx4EVWm6FZqzY7hT9Pqn6NcW/e2BTCHwAgYPj8NaywsDANGjRIhYWF9jGbzabCwkKlpaU1+zg2m83h8q0kPfnkk3r00UdVUFCgwYMHn/MY4eHhioqKcviBb8rftk+DHv2n3tteaR976m9Puwx/Ky8fbQ9/nTuEOrwWHx2h524dqGv70tcPABA4fL4CKEmZmZmaNGmSBg8erKFDhyovL0/Hjh3T5MmTJTVU5vbu3atXXnlFUkPPwIsuukh9+vSRJK1bt04LFy7UfffdZz/mggULNHfuXK1cuVJJSUmqrGwICj/60Y/0ox/9yMufEK3pfPbvXXLLQAUFWexPCNPaBQAQiPwiAE6YMEEHDhzQ3LlzVVlZqQEDBqigoMD+YEhFRYW++eYb+3ybzabs7GyVl5crJCREPXv21IIFCzRt2untvJ577jnV19frpptucviz5s2bp5ycHK98LrQuq83Qnwt3OoQ/d8Fv4MxXdbhjtMNYQnSEhvXsSuADAAQ8v+gD6KvoI+Q7CkorlPNumSprWr6N21Iu9QKAKfD97ScVQKApjdu4tWQnD0mKjgjWgpsuJ/wBAEyDAAi/c+ZOHjGR4cp5t2Ebt051x7Q9b4LL97gLf4Mu7qy/TBvOZV8AgKkQAOE33O3kIXle9bNYpClXJuvh69jJAwBgPgRA+IX8bRV68M1tOlp3ymF86idv6qGPXnSa/8KgG/T7jKkuj/VfA7tp/vj+7OQBADAtAiB8nqu2LpLnVT9JmnY1+/cCAEAAhE/L37av2T39hty7XAd+dIHL17p0DNVj4/ppTH8e9AAAgAAIn2W1GZrzTqnDWEuqfvdnXKIZI3vxoAcAAD8gAMKnnPmE78HaOh0+1vCwR0uCX0J0hOaNTaG9CwAAZyEAwmfkb6vQnHdKdfhYvX0s/FS9vnhqvMv5Z4e/+KhwPXXzAB08Wsc2bgAANIEACJ9wPvv3Nsq54TKl94pp9bUBABBo6IOBdnf2gx7Xf77OZfh7YdANLsNf5w4hbOMGAIAHqACiXTTe61dZc0Jz39luH/e06nd9/wT96ZdXcKkXAAAPEADhdQWlFcpdU6aK6hP2sbXPT1WP/+xzmjv87he0LyrWabxLZKgeu7GvxvS/sE3XCgBAICIAwiusNkMbdx3Sik/26O+lVQ6vNbfq98h1lyqmUzgPeAAAcJ4IgGhzBaUVynpru44cb/n+vV0jw/Tr9GRCHwAArYAAiDZVUFqh6Ss2O4wF2aza/ccbXc53d6/fozf2JfwBANBKCIBoE1aboY27D2n2m9scxlu6fy9buAEA0HoIgGh1rh7yuHT/bv39xfuc5j6XepMW/PTXLo/Dgx4AALQNAiBaVUFphe5esVnGGWPNrfpZJHWJDNOc6y5VfHQHHvQAAKCNEADRaqw2Q7lryuzhL+ujFzX9kzed5g27+yVVRrneseMPv+hLQ2cAANoYARCtpqT8sP2yr6f3+iVER2je2BTCHwAAXkAARIs17uaxv/aEYjtFqLLmRIse8rg/o7dmjOzN5V4AALyEAIgWcXrQwzC058mxTvMOdOysITNXuDzGBR1DNX98P6p+AAB4GQEQzdZY8Xu/rFIvfLzHPu5J1e9H4cG6PS1J6b1iNKxHV6p+AAC0AwIgmsVVa5fu1VUqWnqn09w5o+7WqwOvcxhrjHkL//tyKn4AALQzAiDOqSWtXbpEhunwsXr7eDwPeQAA4DMIgHCrcTePrDe328PfxK0Fmv+PxU5zz27t8sgPvfwaHxChpx8AAL6DAAiXXF3y9eRev/joDkrr2bXN1gcAAFqOAAgnZ1/yfefl+3V55U6neUkPrpEsjlU9ixou9w5N7tL2CwUAAC1CAISk00/4Vtac0KPvfdYQ/ty0dtnTOUE/nbbMabwxCs4bm8LlXgAAfBgBEOd9ubcRD3oAAOAfCIAm5a6nX+fva7T1mVuc5j/wf2bp9f6jXB7rzvQkZaTE86AHAAB+ggBoQq4qfhL79wIAYBYEQJNx1dNv4Hef661XH3CaO+Te5Trwowucxjt3DNWSiQM1rCc7eQAA4I8IgCZitRnKXVPmUUPnMzVGvSfG91N67xin1wEAgH8gAJpA/Smblhfv0Sflh+2Xfd01dHbV2qURD3kAABAYCIABbn5+mZatL5ftjLKfq6rfqwOu1cOjZziMWdSwpducH3b14CEPAAACAwEwgM3PL9P/rCu3/77szd9r1FclTvOautz7h1/0peIHAECAIQAGqPpTNi1b3xD+wk6d1JdP/cJpzvhf/VGbu1/q8v1c7gUAIHARAAPU8uI9shnSk/l5unn7B06vu2vtQk8/AAACHwEwQB3c/Y3Le/0G3LdSRzpEOY3T0w8AAPMgAAaixETN/u47h6Enr75dz6bd7DR13IALNWHIRVT8AAAwEQJgIPn3v6WhQ52G3bV2CbJIT950ucJCgryxOgAA4CMIgIHCRcB7LXepZh/v7vYtd12VTPgDAMCE+Pb3dy+/7Lpxs2FowtxpmnZ1ss6+shtkkaZdnazsMSneWSMAAPApFsMwjHNPgys1NTWKjo5WdXW1oqKcH6xoLVaboZLyw9pfe0KxnSIa7tezWaXQUOfJO3dKvXo5DDXuBPL14eO6uEtH3ZaWROUPAGBa3vr+9mVcAvZhVpuhxWu/0osfl+vI9yft409/uFTjS85q43LNNdLatS6PExYSpDuv6tGWSwUAAH7Eb8pAS5YsUVJSkiIiIpSamqqSEucdLRoVFRUpPT1dXbt2VYcOHdSnTx8tWrTIad7rr7+uPn36KCIiQv369VN+fn5bfgSPFJRWaNBj72vRB1/aw1+X49Xas+B65/BXU+M2/AEAAJzNLwLga6+9pszMTM2bN0+bN2/W5ZdfrtGjR2v//v0u50dGRmrGjBlat26dPv/8c82ZM0dz5szR888/b5+zYcMGTZw4UXfeeae2bNmicePGady4cSotLfXWx3KroLRC01ds1pHjp6t+a5+fqs1//pXDvGU/u11Wq03q1MnbSwQAAH7ML+4BTE1N1ZAhQ7R48WJJks1mU2JiombOnKmsrKxmHWP8+PGKjIzU8uXLJUkTJkzQsWPH9N57p6tpw4YN04ABA7R06dJmHbMt7iGw2gxduWCtKqpPSJK6HjuiTYtvdZrX2Npl1V3DlNaza6v82QAAmAH3APpBBbC+vl6bNm1SRkaGfSwoKEgZGRkqLi5u1jG2bNmiDRs2aMSIEfax4uJih2NK0ujRo5t9zLZSUn7YHv4kafa/XnJ4fcr4Rxq2cfvhyd/9tScEAADgCZ9/COTgwYOyWq2Ki4tzGI+Li9OOHTuafG/37t114MABnTp1Sjk5OZoyZYr9tcrKSpfHrKysdHu8uro61dXV2X+vqanx5KM0y9mB7qMegzX28/V6eeB1euKaO5zmx3aKaPU1AACAwObzAfB8rF+/XkePHtXGjRuVlZWlXr16aeLEiS0+3vz585Wbm9uKK3R2dqDL73Ol8vtc6XJuQnRDSxgAAABP+HwAjImJUXBwsKqqqhzGq6qqFB8f3+R7k5OTJUn9+vVTVVWVcnJy7AEwPj7e42NmZ2crMzPT/ntNTY0SExM9+jznMjS5ixKiI1RZfUJN3ZxpkTRvbAr79wIAAI/5/D2AYWFhGjRokAoLC+1jNptNhYWFSktLa/ZxbDabw+XbtLQ0h2NK0vvvv9/kMcPDwxUVFeXw09qCgyyaN7Zhhw530e6CjqF67taBurZvQqv/+QAAIPD5fAVQkjIzMzVp0iQNHjxYQ4cOVV5eno4dO6bJkydLaqjM7d27V6+88oqkhp6BF110kfr06SNJWrdunRYuXKj77rvPfsxZs2ZpxIgReuqpp3Tddddp9erV+vTTTx1axbSXa/sm6LlbByp3TZnDAyGdO4RqcnqSZozsTeUPAAC0mF8EwAkTJujAgQOaO3euKisrNWDAABUUFNgf4qioqNA333xjn2+z2ZSdna3y8nKFhISoZ8+eWrBggaZNm2afM3z4cK1cuVJz5szRQw89pN69e+vtt99W3759vf75XLm2b4JGpcQ7bwFH8AMAAOfJL/oA+ir6CAEA4H/4/vaDewABAADQugiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYDAEQAADAZAiAAAAAJkMABAAAMBkCIAAAgMkQAAEAAEyGAAgAAGAyBEAAAACTIQACAACYTEh7L8CfGYYhSaqpqWnnlQAAgOZq/N5u/B43IwLgeaitrZUkJSYmtvNKAACAp2praxUdHd3ey2gXFsPM8fc82Ww27du3T506dZLFYmn149fU1CgxMVHffvutoqKiWv34OI1z7V2cb+/hXHsP59p7zvdcG4ah2tpaXXjhhQoKMufdcFQAz0NQUJC6d+/e5n9OVFQU/zLxEs61d3G+vYdz7T2ca+85n3Nt1spfI3PGXgAAABMjAAIAAJhMcE5OTk57LwLuBQcH66c//alCQrha39Y4197F+fYezrX3cK69h3N9fngIBAAAwGS4BAwAAGAyBEAAAACTIQACAACYDAEQAADAZAiA7WzJkiVKSkpSRESEUlNTVVJS0uT8jz76SAMHDlR4eLh69eqll156yTsLDQCenOu33npLo0aN0o9//GNFRUUpLS1N//jHP7y4Wv/m6d/rRh9//LFCQkI0YMCANl5hYPH0fNfV1enhhx/WxRdfrPDwcCUlJemFF17w0mr9m6fn+tVXX9Xll1+ujh07KiEhQXfccYcOHTrkpdX6r3Xr1mns2LG68MILZbFY9Pbbb5/zPXw/eshAu1m9erURFhZmvPDCC8Znn31m3HXXXUbnzp2Nqqoql/N3795tdOzY0cjMzDTKysqMP//5z0ZwcLBRUFDg5ZX7H0/P9axZs4wFCxYYJSUlxpdffmlkZ2cboaGhxubNm728cv/j6blu9J///Mfo0aOH8fOf/9y4/PLLvbRa/9eS833DDTcYqampxvvvv2+Ul5cbGzZsMIqKiry4av/k6bkuKioygoKCjD/96U/G7t27jfXr1xuXXXaZ8Ytf/MLLK/c/+fn5xsMPP2y89dZbhiTjr3/9a5Pz+X70HAGwHQ0dOtS499577b9brVbjwgsvNObPn+9y/oMPPmhcdtllDmMTJkwwRo8e3abrDASenmtXUlJSjNzc3LZYXkBp6bmeMGGCMWfOHGPevHkEQA94er7//ve/G9HR0cahQ4e8tcSA4em5/uMf/2j06NHDYeyZZ54xunXr1qbrDDTNCYB8P3qOS8DtpL6+Xps2bVJGRoZ9LCgoSBkZGSouLnb5nuLiYof5kjR69Gi389GgJef6bDabTbW1terSpUtbLTMgtPRcv/jii9q9e7fmzZvnjWUGjJac73fffVeDBw/Wk08+qW7duumSSy7R7373O33//ffeWrZfasm5TktL07fffqv8/HwZhqGqqiq9/vrrGjNmjLeWbRp8P3qOANhODh48KKvVqri4OIfxuLg4VVZWunxPZWWly/k1NTX8y7sJLTnXZ1u4cKGOHj2qm2++uS2WGDBacq537typrKwsrVixgo7+HmrJ+d69e7eKiopUWlqqv/71r8rLy9Mbb7yhe+65xxtL9lstOdfp6el69dVXNWHCBIWFhSk+Pl6dO3fWkiVLvLFkU+H70XMEQOAcVq5cqdzcXP3lL39RbGxsey8noFitVt1yyy3Kzc3VJZdc0t7LMQWbzSaLxaJXX31VQ4cO1ZgxY/T000/r5Zdf5ouylZWVlWnWrFmaO3euNm3apIKCAu3Zs0fTp09v76UB4j+320lMTIyCg4NVVVXlMF5VVaX4+HiX74mPj3c5PyoqSh06dGiztfq7lpzrRqtXr9aUKVP0+uuvO11egDNPz3Vtba0+/fRTbdmyRTNmzJDUEFAMw1BISIj++c9/aldLcWQAAAMvSURBVOTIkV5Zuz9qyd/thIQEdevWTdHR0faxSy+9VIZh6LvvvlPv3r3bdM3+qiXnev78+Ro+fLgeeOABSVL//v0VGRmpq666So899pgSEhLafN1mwfej56gAtpOwsDANGjRIhYWF9jGbzabCwkKlpaW5fE9aWprDfEl6//333c5Hg5aca0latWqVJk+erFWrVum6667zxlL9nqfnOioqStu3b9fWrVvtP9OnT9dPfvITbd26Vampqd5cvt9pyd/t9PR07du3T0ePHrWPffnllwoKClL37t3bfM3+qiXn+vjx4063NQQHB0uSDMNou8WaEN+PLdC+z6CY2+rVq43w8HDjpZdeMsrKyoypU6canTt3NiorKw3DMIysrCzjtttus89vfMz9gQceMD7//HNjyZIlPObeTJ6e61dffdUICQkxlixZYlRUVNh/jhw50l4fwW94eq7PxlPAnvH0fNfW1hrdu3c3brrpJuOzzz4z/vWvfxm9e/c2pkyZ0l4fwW94eq5ffPFFIyQkxHj22WeNXbt2GUVFRcbgwYONoUOHttdH8Bu1tbXGli1bjC1bthiSjKefftrYsmWL8fXXXxuGwfdjayAAtrM///nPxkUXXWSEhYUZQ4cONTZu3Gh/bdKkScaIESMc5n/44YfGgAEDjLCwMKNHjx7Giy++6N0F+zFPzvWIESMMSU4/kyZN8v7C/ZCnf6/PRAD0nKfn+/PPPzcyMjKMDh06GN27dzcyMzON48ePe3nV/snTc/3MM88YKSkpRocOHYyEhATjV7/6lfHdd995edX+58MPP2zy38F8P54/i2FQhwYAADAT7gEEAAAwGQIgAACAyRAAAQAATIYACAAAYDIEQAAAAJMhAAIAAJgMARAAAMBkCIAAAAAmQwAEAAAwGQIgAACAyRAAAQAATIYACAAAYDIEQAAAAJMhAAIAAJgMARAAAMBkCIAAAAAmQwAEAAAwGQIgAACAyRAAAQAATIYACAAAYDIEQAAAAJMhAAIAAJgMARAAAMBkCIAAAAAmQwAEAAAwGQIgAACAyRAAAQAATIYACAAAYDIEQAAAAJMhAAIAAJjM/wey3tT9HWLShgAAAABJRU5ErkJgggA=" alt="" width="473" height="349" />
--------------------------------------
说明:本列为前期学习时记录,为基本概念和操作,不涉及深入部分。文字部分参考在文中注明,代码参考莫凡
TensorFlow简易学习[2]:实现线性回归的更多相关文章
- TensorFlow简易学习[3]:实现神经网络
TensorFlow本身是分布式机器学习框架,所以是基于深度学习的,前一篇TensorFlow简易学习[2]:实现线性回归对只一般算法的举例只是为说明TensorFlow的广泛性.本文将通过示例Ten ...
- TensorFlow简易学习[1]:基本概念和操作示例
简介 TensorFlow是一个实现机器学习算法的接口,也是执行机器学习算法的框架.使用数据流式图规划计算流程,可以将计算映射到不同的硬件和操作系统平台. 主要概念 TensorFlow的计算可以表示 ...
- TensorFlow 学习笔记(1)----线性回归(linear regression)的TensorFlow实现
此系列将会每日持续更新,欢迎关注 线性回归(linear regression)的TensorFlow实现 #这里是基于python 3.7版本的TensorFlow TensorFlow是一个机器学 ...
- (转) TensorFlow深度学习,一篇文章就够了
TensorFlow深度学习,一篇文章就够了 2016/09/22 · IT技术 · TensorFlow, 深度学习 分享到:6 原文出处: 我爱计算机 (@tobe迪豪 ) 作者: 陈迪 ...
- TensorFlow深度学习,一篇文章就够了
http://blog.jobbole.com/105602/ 作者: 陈迪豪,就职小米科技,深度学习工程师,TensorFlow代码提交者. TensorFlow深度学习框架 Google不仅是大数 ...
- windows下Anaconda3配置TensorFlow深度学习库
Anaconda3(python3.6)安装tensorflow Anaconda3中安装tensorflow3是非常简单的,仅需通过 pip install tensorflow 测试代码: imp ...
- 问题集录--TensorFlow深度学习
TensorFlow深度学习框架 Google不仅是大数据和云计算的领导者,在机器学习和深度学习上也有很好的实践和积累,在2015年年底开源了内部使用的深度学习框架TensorFlow. 与Caffe ...
- 没有博士学位,照样玩转TensorFlow深度学习
教程 | 没有博士学位,照样玩转TensorFlow深度学习 机器之心2017-01-24 12:32:22 程序设计 谷歌 操作系统 阅读(362)评论(0) 选自Codelabs 机器之心编译 参 ...
- HTML DOM简易学习笔记
文字版:https://github.com/songzhenhua/github/blob/master/HTML DOM简易学习笔记.txt 学习地址:http://www.w3school.co ...
随机推荐
- Python和SQL Server 2017的强大功能
Python和SQL Server 2017的强大功能 摘要: 源:https://www.red-gate.com/simple-talk/sql/sql-development/power-pyt ...
- CoreData和SQLite多线程访问时的线程安全问题
数据库读取操作一般都是多线程访问的.在对数据进行读取时,我们要保证其当前状态不能被修改,即读取时加锁,否则就会出现数据错误混乱.IOS中常用的两种数据持久化存储方式:CoreData和SQLite,两 ...
- RoportNG报表显示中文乱码和TestNG显示中文乱码实力解决办法
最近在进军测试自动化框架学习阶段,但无意间总是会伴随小问题的困扰,比如中文乱码,而导致显示总是不舒服,个人觉得,就一定要解决,似乎有点点强迫症.所以遇到RoportNG报表显示中文乱码和TestNG显 ...
- win10 3dmax 激活后反复激活和激活码无效问题
我也是遇到这个问题在网上找答案,像什么断网,清理注册表,删除某个.dat文件 各种试了好多都没管用 弄这个弄了五六个小时才总算成功 心累 现在我总结一下这些方法 我是第一条成功的 其他的我试着都没用 ...
- nexus3 添加第三方本地文件jar到仓库
因为nexus3和nexus2手动上传第三方jar有点区别 故记录一下. 如上传京东 open-api-sdk-2.0.jar 首先创建一个目录 方便执行上传的时候url参数 也可以不创建 mkdir ...
- 墨卡托投影坐标系(Mercator Projection)原理及实现C代码
墨卡托投影是一种"等角正切圆柱投影",荷兰地图学家墨卡托(Mercator)在1569年拟定:假设地球被围在一个中空的圆柱里,其赤道与圆柱相接触,然后再假想地球中心有一盏灯,把球面 ...
- Fiddler使用总结(一)
与后端数据通信是前端日常开发的重要一环,在与后端接口联调的时候往往需要通过查看后端返回的数据进行调试.如果在PC端,Chrome自带的DevTools就已经足够用了,Network面板可以记录所有网络 ...
- [maven(1)]myeclipse2014下如何配置maven
1.maven工程下载,解压压缩包到某一目录中 2.配置环境变量 在电脑环境变量中新建M2_HOME M2_HOME:D:\MAVEN\apache-maven-3.3.9(类似Java_Home) ...
- 深入理解final和static关键字
深入理解final和static关键字 参考:http://blog.csdn.net/qq1028951741/article/details/53418852 final关键字 final关键字可 ...
- Java基础总结--IO总结2
1.键盘录入--Java具有特定的对象封装这些输入输出设备在System类定义 in-InputStream类型和out-PrintStream类型成员变量阻塞是方法:read()无数据就阻塞wind ...
