leetcode#42 Trapping rain water的五种解法详解

leetcode#42 Trapping rain water

这道题十分有意思，可以用很多方法做出来，每种方法的思想都值得让人细细体会。

42. Trapping Rain Water
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

For example,
Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.

Solution 1:

通过分别计算每一坐标i上有多少水，进而将其相加得到答案。

问题是我们如何知道每一坐标i上有多少水呢？仔细思考，其实只有出现“两高夹一矮”才可能会存到水，如下图所示。

进而，我们可以想到：每一坐标i上存多少水是由 1.其自身高度 2.它左边的最高高度left_most 3.它右边的最高高度right_most三种因素决定的。

当 min{ left_most, right_most} 小于或等于其自身高度时，它能存的水就是0，比如array[1]=1,其left_most= array[0]=0, 其right_most=array[7]=3, min{left_most, right_most}=left_most=0< height= array[1]=1，这也就是说坐标1 存不了水。

当min{ left_most,right_most} 大于其自身高度时，这时这三者间出现了“两高夹一矮”的情况，故其能存水，而且其存水数= min{left_most,right_most} - height。

我们分别来对一些坐标进行验证：

坐标1，存水数=0.//正确

坐标2，leff_most=1,right_most=3，存水数=left_most-height=1-0=1.//正确

坐标3，left_most=1,right_most=3,min{left_most,right_most}=1=height，存水数=0.//正确

读者可以对每个坐标进行验证，会发现以上结论皆是正确的。所以，现在我们的solution就出来了，我们只需要求出每个坐标对应的left_most和right_most，再把存水数相加，就是总的存水数了。

所以，很朴素自然的一个想法就是，遍历一遍数组，对每个数组元素遍历左边一次求出left_most，遍历右边一次求出right_most。

代码如下，

 
//29ms 6.36%
//complexity: O(N^2)
int trap(vector<int>& height)
{
    int ans = 0;
    int size = height.size();
    for (int i = 1; i < size - 1; i++) {
        int max_left = 0, max_right = 0;
        for (int j = i; j >= 0; j--) { //Search the left part for max bar size
            max_left = max(max_left, height[j]);
        }
        for (int j = i; j < size; j++) { //Search the right part for max bar size
            max_right = max(max_right, height[j]);
        }
        ans += min(max_left, max_right) - height[i];
    }
    return ans;
}

Solution 2：

在solution 1里，我们已经知道只要求出left_most和right_most，就可以求出答案，那能不能优化一下求这两个数的过程呢？当然是可以的，我们只需要左遍历一次数组，右遍历一次数组，即可得到left_most和right_most。

/*Solution2: 上一种方法其实有优化的空间
通过两次for循环可分别求得left_most和right_most，第三次for循环即可求得sum，
complexity: O(n)
*/
int trap(vector<int>& height)
{
    if(height == null)
        return ;
    int ans = ;
    int size = height.size();
    vector<int> left_max(size), right_max(size);
    left_max[] = height[];
    for (int i = ; i < size; i++) {
        left_max[i] = max(height[i], left_max[i - ]);
    }
    right_max[size - ] = height[size - ];
    for (int i = size - ; i >= ; i--) {
        right_max[i] = max(height[i], right_max[i + ]);
    }
    for (int i = ; i < size - ; i++) {
        ans += min(left_max[i], right_max[i]) - height[i];
    }
    return ans;
}

Solution 3：

这里再介绍一种优化方法，双指针法，在数组首尾分别创建一个指针，两指针相见时结束循环。

int trap(vector<int>& height)
{
    int left = , right = height.size() - ;
    int ans = ;
    int left_max = , right_max = ;
    while (left < right) {
        if (height[left] < height[right]) {
            height[left] >= left_max ? (left_max = height[left]) : ans += (left_max - height[left]);
            ++left;
        }
        else {
            height[right] >= right_max ? (right_max = height[right]) : ans += (right_max - height[right]);
            --right;
        }
    }
    return ans;
}

Solution 4：

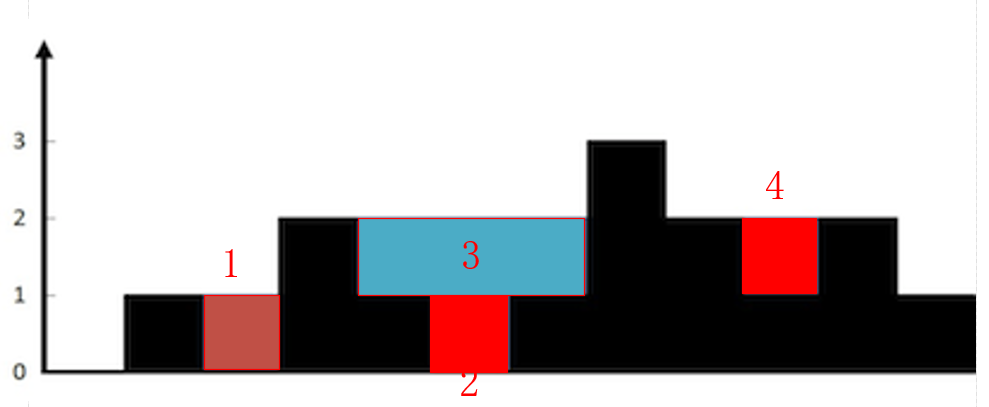
既然可以纵向的求存水数，那我们能不能一层一层的求存水数呢？

这是第一层，当我们遇到一个空的，且不在边界，存水数+1，所以第一层我们在i=2,i=5 时分别+1.

第二层，存水数+4，依次类推，最终可以求出答案。

代码笔者就不给了，读者有兴趣的可以自己写来试试。

Soluton 5：

这是在leetcode中solution给出的一种很新颖的解法，利用了栈的结构，通过维护一个非递增栈来得到答案。

本质思想还是利用了要存水必须是“两高夹一矮”这个特点，只不过这里是用非递增栈来实现。

下面定义一些符号以便理解：

stack[-1] 栈顶元素

stack[-2] 栈顶的下面一个元素（即倒数第二个元素）

solution4的整个算法是这么实现的：遍历数组，遇到一个元素时，将其与栈顶元素比较，如果其小于等于栈顶元素，直接压栈，将其放入栈中（为维护非递增栈的结构,不能将比栈顶元素大的元素压栈），

若是其大于栈顶元素，此时一定形成了一个“两高夹一矮”局面，因为栈是非递增栈，所以 stack[-1]<stack[-2],又 current>stack[-1],所以是一个“两高夹一矮”局面，此时算完存水数后栈顶元素出栈，继续判断，

递归处理即可。

在上例中整个过程是这样的。

step0: 0不入栈

step1: 1>0 array[1] 入栈 栈：[1]

step2: 0<stack[-1]=1 入栈 栈：[1,0]

step3: 2>stack[-1]=0 存水数+1，0出栈，2>stack[-1]=1, 此时stack内元素不足2，不足以形成“两高夹一矮”局面, 1出栈，2入栈 栈：[2]

step4: 1<stack[-1]=2 1入栈 栈：[2,1]

step5: 0<stack[-1]=1 0入栈 栈：[2,1,0]

step6: 1>stack[-1]=0 存水数+1，0出栈 1=stack[-1] 1入栈 栈：[2,1,1]

step7: 3>stack[-1]=1 存水数+0，1出栈 3>stack[-1]=1 存水数+3,1出栈 3>stack[-1]=2 存水数+0 2出栈 3入栈 栈：[3]

step8: 2<stack[-1] 2入栈 栈：[3,2]

step9: 1<stack[-1] 1入栈 栈：[3,2,1]

step10: 2>stack[-1] 存水数+1 1出栈 2入栈 栈：[3,2,2]

step 11:1<stack[-1] 入栈 栈：[3,2,2,1]

done

/*Solution4
Stack solution
这个solution利用了栈结构，通过维护一个非递增栈，一步一步算出ans
*/

int trap(vector<int>& height)
{
    int ans = , current = ;
    stack<int> st;
    while (current < height.size()) {
        while (!st.empty() && height[current] > height[st.top()]) {
            int top = st.top();
            st.pop();
            if (st.empty())
                break;
            int distance = current - st.top() - ;
            int bounded_height = min(height[current], height[st.top()]) - height[top];
            ans += distance * bounded_height;
        }
        st.push(current++);
    }
    return ans;
}