noip2016十连测题解

以下代码为了阅读方便，省去以下头文件：

#include <iostream>
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <time.h>
#include <stdlib.h>
#include <string>
#include <bitset>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <algorithm>
#include <sstream>
#include <stack>
#include <iomanip>
using namespace std;
#define pb push_back
#define mp make_pair
typedef pair<int,int> pii;
typedef long long ll;
typedef double ld;
typedef vector<int> vi;
#define fi first
#define se second
#define fe first
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);}
#define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);}
#define es(x,e) (int e=fst[x];e;e=nxt[e])
#define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e])

D1 P1

两个长度都为n的字符串，修改不超过k次（一次只能修改任意一串的任意一个字符）使最长公共子串最长。n<=300，k<=350。

枚举最长公共子串在两串中的开头，往后看匹不匹配，不匹配就修改。

#define SZ 666666
int n,k;
char sa[SZ],sb[SZ];
int main()
{
    FO(master)
    scanf("%d%d%s%s",&n,&k,sa,sb);
    int ans=0;
    for(int a=0;a<n;a++)
    {
        for(int b=0;b<n;b++)
        {
            int cur=0;
            for(int l=1;a+l<=n&&b+l<=n;l++)
            {
                cur+=(sa[l+a-1]!=sb[l+b-1]);
                if(cur>k) break;
                ans=max(ans,l);
            }
        }
    }
    printf("%d\n",ans);
}

D1 P2

给出一个n个点的图的邻接矩阵，求有多少条简单路径恰好经过了4个点。n<=1500。

我们枚举一条边作为简单路径中间的一条边，那么对答案的贡献就是(d1-1)*(d2-1)*2类似这样。

这时候我们发现三元环好像会被计算若干次，扣掉就行了。三元环的个数只要枚举一条边，两个端点的邻接矩阵and在一起看一下有多少个1就行。bitset一波。

#define SZ 666666
int n;
ll cc[SZ];
char rp[1505][1505];
bitset<1503> bs[1505];
int main()
{
    FO(tour)
    scanf("%d\n",&n);
    for(int i=1;i<=n;i++) gets(rp[i]+1);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            cc[j]+=(rp[i][j]=='1');
            bs[i][j]=rp[i][j]-'0';
        }
    }
    ll ans=0,cyc=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=i+1;j<=n;j++)
        {
            if(rp[i][j]!='1') continue;
            ans+=(cc[i]-1)*(cc[j]-1)*2;
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=i+1;j<=n;j++)
            if(rp[i][j]=='1') cyc+=(bs[i]&bs[j]).count();
    }
    cout<<ans-cyc*2<<"\n";
}

D1 P3

有n个点，编号为1~n，开始有m条单向边。每个点有一个编码val，如果$val_i~and~val_j=val_j$，那么i->j也有一条单向边。边权都为1，求1号点到每一个点的距离。n<=20W，m<=30W，1<=val<2^20。

我们考虑把每个val建一个点，假设对于一个val的位置为val+r，i->val[i]+r连一条权值为1的边，val[i]+r->i连一条权值为0的边，那么我们只要让val里面连的那些边边权为0就行了。

val里面连边暴力连显然比较蠢，我们只连二进制相差一位的val，这样传递一下就相当于连了所有变了。

至于边权为0和1的最短路怎么跑...2^20个点，spfa显然过不去。有一种技巧是边权为0的扩展完塞到队头，边权为1的塞到队尾，这样bfs就可以了。

#define SZ 11500003
int N,n,m,vs[233333];
int M=0,fst[1281909],vb[SZ],nxt[SZ];
bool vc[SZ];
void ad_de(int a,int b,int c)
{++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}
int r=0,lim=1<<20;
int dist[1281909];
#define P 2097151
int qs[P+3];
void spfa()
{
    memset(dist,127/3,sizeof(dist));
    dist[1]=0;
    int h=0,t=0; qs[t++]=1;
    while(h^t)
    {
        int x=qs[h++]; h&=P;
        if(dist[x]>=dist[0]) continue;
        for es(x,e)
        {
            int b=vb[e],c=vc[e];
            if(dist[b]<=dist[x]+c) continue;
            dist[b]=dist[x]+c;
            if(c) qs[t++]=b, t&=P;
            else qs[h=(h-1)&P]=b;
        }
    }
}
char ch,B[1<<15],*S=B,*T=B;
#define getc() (S==T&&(T=(S=B)+fread(B,1,1<<15,stdin),S==T)?0:*S++)
#define isd(c) (c>='0'&&c<='9')
int aa,bb;int F(){
    while(ch=getc(),!isd(ch)&&ch!='-');ch=='-'?aa=bb=0:(aa=ch-'0',bb=1);
    while(ch=getc(),isd(ch))aa=aa*10+ch-'0';return bb?aa:-aa;
}
#define gi F()
#define BUFSIZE 300000
namespace fob {char b[BUFSIZE]={},*f=b,*g=b+BUFSIZE-2;}
#define pob (fwrite(fob::b,sizeof(char),fob::f-fob::b,stdout),fob::f=fob::b,0)
#define pc(x) (*(fob::f++)=(x),(fob::f==fob::g)?pob:0)
struct foce {~foce() {pob; fflush(stdout);}} _foce;
namespace ib {char b[100];}
inline void pint(int x)
{
    if(x==0) {pc(48); return;}
    if(x<0) {pc('-'); x=-x;}
    char *s=ib::b;
    while(x) *(++s)=x%10, x/=10;
    while(s!=ib::b) pc((*(s--))+48);
}
int main()
{
    FO(walk)
    n=N=gi; m=gi;
    for(int i=1;i<=n;i++) vs[i]=gi;
    for(int i=1;i<=m;i++)
    {
        int a=gi,b=gi;
        ad_de(a,b,1);
    }
    r=n+1; n+=lim;
    for(int i=1;i<=N;i++) ad_de(i,vs[i]+r,1);
    for(int i=1;i<=N;i++) ad_de(vs[i]+r,i,0);
    int m1=M;
    for(int j=0;(1<<j)<lim;j++)
    {
        for(int i=0;i<lim;i++)
        {
            int nx=i|(1<<j);
            if(i==nx||nx>=lim) continue;
            ad_de(nx+r,i+r,0);
        }
    }
    spfa();
    for(int i=1;i<=N;i++)
    {
        if(dist[i]>=dist[0]) dist[i]=-1;
        pint(dist[i]); pc(10);
    }
}

D2 T1

给定m个不同正整数a1~am，对于0~m的每一个k，求[1,n]中有多少个数是a中恰好k个数的倍数。m<=200，1<=n,a<=10^9。

枚举每个数的约数即可，下面这个代码写的比较智障。

vector<pii> fj(int x)
{
    vector<pii> vec;
    for(int i=2;i*i<=x;i++)
    {
        if(x%i) continue;
        pii cur=pii(i,0);
        while(x%i==0) ++cur.se, x/=i;
        vec.pb(cur);
    }
    if(x>1) vec.pb(pii(x,1));
    return vec;
}
vector<pii> pp;
vi yy;
void dfs(int dep=0,int c1=1)
{
    if(dep==pp.size())
    {
        yy.push_back(c1);
        return;
    }
    int a=pp[dep].fi,b=pp[dep].se;
    for(int j=0;j<=b;j++)
    {
        dfs(dep+1,c1);
        c1*=a;
    }
}
vi yss(int x)
{
    yy.clear();
    pp=fj(x);
    dfs();
    return yy;
}
int n,m,a[SZ];
set<int> si;
int cc[SZ];
int cnt(int s)
{
    int ans=0;
    for(int i=1;i<=m;i++) ans+=(a[i]%s==0);
    return ans;
}
int main()
{
    FO(div)
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++) scanf("%d",a+i);
    for(int i=1;i<=m;i++)
    {
        vi t=yss(a[i]);
        for(int j=0;j<t.size();j++) si.insert(t[j]);
    }
    for(set<int>::iterator p=si.begin();p!=si.end();++p)
    {
        int g=*p;
        if(g>n) continue;
        ++cc[cnt(g)];
    }
    int sum=n;
    for(int i=0;i<=m;i++) sum-=cc[i];
    cc[0]+=sum;
    for(int i=0;i<=m;i++) printf("%d\n",cc[i]);
}

D2 T2

有n个商店，每个商店卖一个物品，一个物品有价格、价值，商店会在某一时间开张。

要进行m次购物，每次购物有一个预算，在某个时间开始，求每次的最大价值，购买之间独立。

n<=300，m<=10W，价格、预算<=10^9，价值、时间<=300。

询问离线后按时间排序。既然价值这么小，我们就用dp[i]表示达到i这么多的价值最少的价格，询问时二分。

#define SZ 666666
int n,m;
struct shop {int c,v,t;}cs[SZ];
struct plan {int t,m,id,ans;}ps[SZ];
bool operator < (shop a,shop b)
{return a.t<b.t;}
bool operator < (plan a,plan b)
{return a.t<b.t;}
bool cid(plan a,plan b)
{return a.id<b.id;}
int W=90000;
ll rp[99999];
int cur=1;
void pt(ll t)
{
    while(cur<=n&&ps[cur].t<t)
    {
        int l=0,r=W;
        while(l<r)
        {
            int m=(l+r+1)>>1;
            if(rp[m]<=ps[cur].m) l=m; else r=m-1;
        }
        ps[cur++].ans=l;
    }
}
int main()
{
    FO(market)
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    scanf("%d%d%d",&cs[i].c,&cs[i].v,&cs[i].t);
    for(int i=1;i<=m;i++)
    scanf("%d%d",&ps[i].t,&ps[i].m), ps[i].id=i;
    sort(ps+1,ps+1+m);
    sort(cs+1,cs+1+n);
    memset(rp,127/3,sizeof(rp)); rp[0]=0;
    for(int i=1;i<=n;i++)
    {
        pt(cs[i].t);
        for(int j=W;j>=cs[i].v;j--)
        rp[j]=min(rp[j],cs[i].c+rp[j-cs[i].v]);
    }
    pt(1e9+3);
    sort(ps+1,ps+1+m,cid);
    for(int i=1;i<=m;i++) printf("%d\n",ps[i].ans);
}

D2 T3

有一棵n个点的树，每条边i有一个限制区间[li,ri]表示速度在[li,ri]才能通过这条边。现在给出m个询问，每次给出一个速度求最长链。n,m<=70000，1<=li<=ri<=n。

首先我们知道我们是可以加边和维护一个森林的直径的。并查集，合并两个联通块时新直径只可能从6个点产生：原来两条直径的端点和接在一起的那条边。此外，我们也可以按照加边的顺序倒着撤销，只要并查集是按秩合并的就可以。

接下来我们考虑对于速度建出一棵线段树，然后那么一个限制区间就可以下放到线段树上的若干个节点，而一个询问针对的是一个叶子节点，满足条件的是这个叶子节点到线段树根上的这些边。那我们在线段树上dfs，进入一个节点的时候加上这个节点的边，出去的时候撤销这些边，这样就行了。

以下的代码没有在bzoj评测机上测过，（很有）可能会被卡常/爆内存。

#define SZ 200003
ll MOD=998244353;
Edg
#define P 19
typedef pair<int,int> pii;
int n,fa[SZ],dep[SZ];
int cc=0,app[SZ],bs[SZ],cx[SZ],c2=0;
pii pp[SZ],minn[SZ][P];
void dfs(int x)
{
    ++cc; app[x]=cc; pp[cc]=pii(dep[x],x); cx[++c2]=x;
    for(int e=fst[x];e;e=nxt[e])
    {
        int b=vb[e]; if(b==fa[x]) continue;
        fa[b]=x; dep[b]=dep[x]+1;
        dfs(b); pp[++cc]=pii(dep[x],x);
    }
}
void build()
{
    for(int i=1;i<=cc;i++) minn[i][0]=pp[i];
    for(int i=1;i<=cc;i++)
    {
        int g=0;
        while((1<<g)<=i) ++g;
        bs[i]=g-1;
    }
    for(int p=1;p<P;p++)
    {
        for(int i=1;i<=cc;i++)
        {
            if(i+(1<<p)-1>cc) break;
            minn[i][p]=min(minn[i][p-1],minn[i+(1<<(p-1))][p-1]);
        }
    }
}
int lca(int a,int b)
{
    a=app[a]; b=app[b];
    if(a>b) swap(a,b);
    int l2=bs[b-a+1];
    return min(minn[a][l2],minn[b-(1<<l2)+1][l2]).second;
}
int dis(int a,int b)
{
    int l=lca(a,b);
    return dep[a]+dep[b]-dep[l]*2;
}
pii mg(pii a,int b)
{
    int s[3]={a.fi,a.se,b};
    pii aa; int ans=-1;
    for(int i=0;i<3;i++)
    {
        for(int j=i+1;j<3;j++)
        {
            int d=dis(s[i],s[j]);
            if(d>ans) ans=d, aa=pii(s[i],s[j]);
        }
    }
    return aa;
}
//a,b为直径，c为衔接处
pii mg(pii a,pii b,pii c)
{
    pii aa=a; int ans=dis(a.fi,a.se);
    {
        int tmp=dis(b.fi,b.se);
        if(tmp>ans) ans=tmp, aa=b;
    }
    int as[3]={a.fi,a.se,c.fi},bs[3]={b.fi,b.se,c.se};
    for(int i=0;i<3;i++)
    {
        for(int j=0;j<3;j++)
        {
            int d=dis(as[i],bs[j]);
            if(d>ans) ans=d, aa=pii(as[i],bs[j]);
        }
    }
    return aa;
}
int m;
struct Tuple {int f; pii z;};
int ans=0,ff[SZ];
pii zj[SZ];
int gf(int x)
{
    return (ff[x]>0)?gf(ff[x]):x;
}
struct Msg
{
int ga,gb,fa,fb;
pii pa,pb;
Msg() {ga=gb=0;}
Msg(int a,int b,int c,int d,pii x,pii y) {ga=a; gb=b; fa=c; fb=d; pa=x; pb=y;}
};
//use the return value to reverse!
Msg uni(int u,int v)
{
    int ga=gf(u),gb=gf(v);
    if(ga==gb) return Msg();
    if(ff[ga]>ff[gb]) swap(ga,gb);
    Msg rt=Msg(ga,gb,ff[ga],ff[gb],zj[ga],zj[gb]);
    pii tmp=mg(zj[ga],zj[gb],pii(u,v));
    zj[ga]=tmp; ff[ga]+=ff[gb]; ff[gb]=ga;
    return rt;
}
void rev(Msg p)
{
    if(!p.ga) return;
    ff[p.ga]=p.fa; ff[p.gb]=p.fb;
    zj[p.ga]=p.pa; zj[p.gb]=p.pb;
}
#define ST 8888888
struct edg {int u,v,l,r;}es[SZ];
namespace seg
{
const int M=131072;
int nx[ST],fs[M+M+3],bb[ST],C=0;
Msg tmp[ST];
void split(int l,int r,int g)
{
    for(l+=M-1,r+=M+1;l^r^1;l>>=1,r>>=1)
    {
        if(~l&1)
        {++C; bb[C]=g; nx[C]=fs[l^1]; fs[l^1]=C;}
        if(r&1)
        {++C; bb[C]=g; nx[C]=fs[r^1]; fs[r^1]=C;}
    }
}
int cm[M+M+3];
int tat[ST];
void dfs(int x,int zjj=0)
{
    for(int e=fs[x];e;e=nx[e])
    {
        int b=bb[e];
        tmp[e]=uni(es[b].u,es[b].v);
        int a=tmp[e].ga;
        if(!a) continue;
        zjj=max(zjj,dis(zj[a].fi,zj[a].se));
    }
    if(x>M) cm[x]=zjj;
    else
    {
        dfs(x*2,zjj);
        dfs(x*2+1,zjj);
    }
    int tn=0;
    for(int e=fs[x];e;e=nx[e]) tat[++tn]=e;
    while(tn) rev(tmp[tat[tn--]]);
}
}
#define BUFSIZE 300000
char ch,B[1<<15],*S=B,*T=B;
#define getc() (S==T&&(T=(S=B)+fread(B,1,1<<15,stdin),S==T)?0:*S++)
#define isd(c) (c>='0'&&c<='9')
int aa,bb;int F(){
    while(ch=getc(),!isd(ch)&&ch!='-');ch=='-'?aa=bb=0:(aa=ch-'0',bb=1);
    while(ch=getc(),isd(ch))aa=aa*10+ch-'0';return bb?aa:-aa;
}
#define gi F()
namespace fob {char b[BUFSIZE]={},*f=b,*g=b+BUFSIZE-2;}
#define pob (fwrite(fob::b,sizeof(char),fob::f-fob::b,stdout),fob::f=fob::b,0)
#define pc(x) (*(fob::f++)=(x),(fob::f==fob::g)?pob:0)
struct foce {~foce() {pob; fflush(stdout);}} _foce;
namespace ib {char b[100];}
inline void pint(int x)
{
    if(x==0) {pc(48); return;}
    if(x<0) {pc('-'); x=-x;}
    char *s=ib::b;
    while(x) *(++s)=x%10, x/=10;
    while(s!=ib::b) pc((*(s--))+48);
}
int main()
{
    FO(speed)
    n=gi, m=gi;
    for(int i=1;i<n;i++)
    {
        es[i].u=gi, es[i].v=gi, es[i].l=gi, es[i].r=gi;
        adde(es[i].u,es[i].v);
    }
    for(int i=1;i<=n;i++) ff[i]=-1, zj[i]=pii(i,i);
    dfs(1); build();
    for(int i=1;i<n;i++)
        seg::split(es[i].l,es[i].r,i);
    seg::dfs(1);
    for(int i=1;i<=m;i++)
    {
        int q=gi;
        pint(seg::cm[q+seg::M]); pc(10);
    }
}

D3 T1

一个长度为n的序列，计算每个连续子序列（子段）的平均数，求第k小的平均数，n<=10W。

二分答案，那么我们要知道平均值<s的子段有几个，我们把所有数都减去s，就是要求和<0的子段个数，即前缀和逆序对个数。

由于懒得离散，写的归并

#define SZ 666666
int n,aa[SZ];
ll k,nx=0;
ld rp[SZ],tmp[SZ];
void fz(int l,int r)
{
    if(l==r) return;
    int tn=0,m=(l+r)>>1;
    fz(l,m); fz(m+1,r);
    int x=l;
    for(int i=m+1;i<=r;i++)
    {
        while(x<=m&&rp[x]<rp[i]) tmp[++tn]=rp[x++];
        nx+=m-x+1; tmp[++tn]=rp[i];
    }
    while(x<=m) tmp[++tn]=rp[x++];
    tn=0;
    for(int i=l;i<=r;i++) rp[i]=tmp[++tn];
}
//平均值<=s的有几个？
ll cnt(ld s)
{
    rp[0]=0;
    for(int i=1;i<=n;i++) rp[i]=rp[i-1]+aa[i]-s;
    nx=0; fz(0,n); return nx;
}
int main()
{
    FO(ave)
    scanf("%d%I64d",&n,&k);
    for(int i=1;i<=n;i++) scanf("%d",aa+i);
    ld l=0,r=1e9+3;
    for(int i=1;i<=80;i++)
    {
        ld m=(l+r)/2;
        if(cnt(m)<k) l=m; else r=m;
    }
    printf("%.4lf\n",l);
}

D3 T2

有一个n*m的网格，要用p种颜色涂色，使每相邻两列都出现了至少q种颜色，求方案数mod 998244353。n,p,q<=100且q<=p，m<=10^9。

我们用dp[a][b]表示前a列，第a列用了b种颜色的方案数，然后我们考虑枚举下一列用了x种新颜色，y种旧颜色，那么dp[a+1][x+y]+=C(b,x)*C(p-b,y)*pal(n,a+b)，其中pal(a,b)表示用恰好b种颜色染a个球的方案数。

注意到这个a是打酱油的，我们拿去矩阵快速幂优化一下。

至于这个pal怎么算，我们枚举在c种颜色中使用了多少种颜色，容斥一发即可。感觉这个东西应该有更优美的算法（这样硬算预处理是立方的），如果有知道的老司机求回答一下：http://stackoverflow.com/questions/39955981/how-to-calculate-the-ways-to-paint-n-different-balls-with-exact-c-different-colo。

#define SZ 666666
ll MOD=998244353;
ll C[233][233],fac[233],P[233][233];
ll pal[233][233];
ll pp[233][233];
int n,m,p,q;
ll qp(ll a,ll b)
{
    a%=MOD; ll ans=1;
    while(b)
    {
        if(b&1) ans=ans*a%MOD;
        a=a*a%MOD; b>>=1;
    }
    return ans;
}
//paint a with b colors
ll sel(int a,int b)
{
    ll ans=0;
    for(int j=1;j<=b;j++)
    {
        if(j%2==b%2) ans+=pp[j][a]*C[b][j]%MOD;
        else ans-=pp[j][a]*C[b][j]%MOD;
        ans%=MOD;
    }
    return ans;
}
int N;
struct mat
{
ll rp[110][110];
ll* operator [] (int p) {return rp[p];}
void clr() {memset(rp,0,sizeof(rp));}
};
mat operator * (mat a,mat b)
{
    mat ans; ans.clr();
    for(int i=0;i<N;i++)
    {
        for(int j=0;j<N;j++)
        {
            ll g=0;
            for(int k=0;k<N;k++)
            g=(g+a[i][k]*b[k][j]%MOD)%MOD;
            ans[i][j]=g;
        }
    }
    return ans;
}
mat dw()
{
    mat ans; ans.clr();
    for(int i=0;i<N;i++) ans[i][i]=1;
    return ans;
}
mat zy;
mat qp(mat x,int g)
{
    mat cur=dw();
    while(g)
    {
        if(g&1) cur=cur*x;
        x=x*x; g>>=1;
    }
    return cur;
}
int main()
{
    FO(color)
    fac[0]=1;
    for(int i=1;i<=200;i++) fac[i]=fac[i-1]*i%MOD;
    for(int i=0;i<=200;i++)
    {
        C[i][0]=1;
        for(int j=1;j<=i;j++) C[i][j]=(C[i-1][j-1]+C[i-1][j])%MOD;
        for(int j=0;j<=i;j++) P[i][j]=C[i][j]*fac[j]%MOD;
    }
    for(int i=0;i<=200;i++)
    {
        pp[i][0]=1;
        for(int j=1;j<=200;j++) pp[i][j]=pp[i][j-1]*i%MOD;
    }
    for(int i=0;i<=200;i++)
    {
        for(int j=1;j<=200;j++) pal[i][j]=sel(i,j);
    }
    cin>>n>>m>>p>>q;
    N=p+1;
    for(int j=0;j<=p;j++)
    {
        for(int a=0;a<=j;a++)
        {
            for(int b=0;b<=p-j;b++)
            {
                if(a+b==0) continue;
                if(j+b>=q);else continue;
                ll &s=zy[j][a+b];
                ll px=C[j][a]*C[p-j][b]%MOD*pal[n][a+b]%MOD;
                s=(s+px)%MOD;
            }
        }
    }
    mat ss=qp(zy,m);
    ll ans=0;
    for(int i=0;i<N;i++) ans+=ss[p][i], ans%=MOD;
    cout<<(ans%MOD+MOD)%MOD<<"\n";
}

D3 T3

有一个长度为n的序列和m个询问，每个询问都是l r x的形式，表示询问l~r位置有多少个数>=x。现在有q次修改，每次要改变一个位置上的数。要求在修改前和每次修改后输出每个询问结果的和，修改强制在线（xor lastans）。

我们考虑一个位置上的数，例如a[s]=g，会对l<=s<=r且g>=s的询问有1的贡献，那么我们只要能数这些询问就可以了，差分完主席树就行。

#define enc
#define SZ 666666
#define S2 6666666
int ch[S2][2],rot[SZ],sum[S2],an=0;
void ins(int r1,int& r2,int l,int r,int p,int q)
{
    if(!r2) r2=++an;
    sum[r2]=sum[r1]+q;
    if(l==r) return;
    int mid=l+r>>1;
    if(p<=mid) ins(ch[r1][0],ch[r2][0],l,mid,p,q), ch[r2][1]=ch[r1][1];
    else ins(ch[r1][1],ch[r2][1],mid+1,r,p,q), ch[r2][0]=ch[r1][0];
}
int query(int r2,int l,int r,int p)
{
    if(l>p) return 0;
    if(r<=p) return sum[r2];
    int mid=l+r>>1,ans=0;
    ans+=query(ch[r2][0],l,mid,min(p,mid));
    if(p>mid) ans+=query(ch[r2][1],mid+1,r,p);
    return ans;
}
int n,m,q,a[SZ];
int ls[SZ],rs[SZ],xs[SZ];
int query(int g,int s)
{return query(rot[g],0,n,s);}
ll aa=0;
struct data
{
    int r,x,g;
    data() {}
    data(int a,int b,int c) {r=a; x=b; g=c;}
};
bool operator < (data a,data b)
{return a.r<b.r;}
data ds[SZ];
int dn=0;
namespace FFF
{
char ch,B[1<<15],*S=B,*T=B;
#define getc() (S==T&&(T=(S=B)+fread(B,1,1<<15,stdin),S==T)?0:*S++)
#define isd(c) (c>='0'&&c<='9')
ll aa,bb;
ll F(){
    while(ch=getc(),!isd(ch)&&ch!='-');ch=='-'?aa=bb=0:(aa=ch-'0',bb=1);
    while(ch=getc(),isd(ch))aa=aa*10+ch-'0';return bb?aa:-aa;
}
}
#define gl FFF::F()
int main()
{
    FO(seq)
    n=gl, m=gl, q=gl;
    //scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;i++) a[i]=gl;//scanf("%d",a+i);
    for(int i=1;i<=m;i++) ls[i]=gl, rs[i]=gl, xs[i]=gl;
    //scanf("%d%d%d",ls+i,rs+i,xs+i);
    for(int i=1;i<=m;i++)
    {
        ds[++dn]=data(ls[i],xs[i],1);
        ds[++dn]=data(rs[i]+1,xs[i],-1);
    }
    sort(ds+1,ds+1+dn);
    int cur=0,cp=1;
    for(int i=0;i<=n+1;i++)
    {
        int p=0;
        while(cp<=dn&&ds[cp].r==i)
        {
            p=0;
            ins(cur,p,0,n,ds[cp].x,ds[cp].g);
            //cout<<i<<" "<<ds[cp].x<<","<<ds[cp].g<<"\n";
            ++cp; cur=p;
        }
        rot[i]=cur;
    }
    for(int i=1;i<=n;i++) aa+=query(i,a[i]);
    ll lans=aa; printf("%I64d\n",lans);
    while(q--)
    {
        ll x=gl,y=gl;
        //scanf("%I64d%I64d",&x,&y);
#ifdef enc
        x^=lans; y^=lans;
#else
//debug only
#warning Encrypt?
#endif
        aa-=query(x,a[x]);
        a[x]=y;
        aa+=query(x,a[x]);
        printf("%I64d\n",aa);
        lans=aa;
    }
}

D4 T1

开始有a个红色，b个黄色，c个蓝色，要求至少x个红色，y个黄色，z个蓝色，每次可以把任何两个同种颜色转化为一个另一种颜色，问是否可行。多组询问，T<=100，0<=a,b,c,x,y,z<=1000000。

如果你不想动脑子，你可以每次把最多的分给最少的，这样暴力就行了。

如果你打算动脑子，我们考虑如果a比x大就有了(a-x)/2的空余，否则就有a-x的需求，只要判需求<=空余就行了。

int tar[3],x[3];
int main()
{
    FO(osiris)
    int T; scanf("%d",&T);
    while(T--)
    {
    scanf("%d%d%d%d%d%d",x,x+1,x+2,tar,tar+1,tar+2);
    while(x[0]<tar[0]||x[1]<tar[1]||x[2]<tar[2])
    {
        int need=0,ok=-1;
        if(x[1]<tar[1]) need=1;
        if(x[2]<tar[2]) need=2;
        if(x[0]-2>=tar[0]) ok=0;
        if(x[1]-2>=tar[1]) ok=1;
        if(x[2]-2>=tar[2]) ok=2;
        if(ok==-1) break;
        x[ok]-=2; x[need]++;
    }
    bool yy=1;
    for(int i=0;i<3;i++) yy&=(x[i]>=tar[i]);
    if(yy) puts("YES"); else puts("NO");
    }
}

D4 T2

给一个n个点m条边的有向图，求有多少个子图（即边集）是无环的，对1e9+7取模。n<=17。

不是很懂题解，待填坑。

D4 T3

给定n，求1<=a,b<=n且lcm(a,b)>n的(a,b)对数mod 1e9+7。

首先我们不妨把求lcm(a,b)>n改为求lcm(a,b)<=n，然后枚举gcd。

设，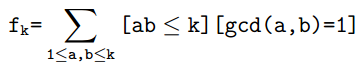

然后设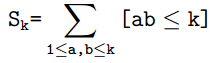，这个不妨设a<=b然后枚举b来算，就可以做到O(sqrt(k))。

那么我们枚举一下gcd，扣掉gcd不为1的就行了：

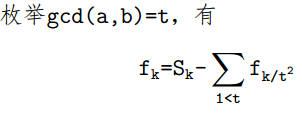
然后老套路，小的情况线筛预处理。那么怎么线筛？

我们考察f(n)-f(n-1)，这部分一定是乘积为n且互质的两个数...那就是2^(n的不同因子个数啊)，因为每个因子只能由一个数取光。

这样我们对于<=n^(2/3)的线筛，用老套路积分可以得到复杂度为O(n^(2/3))。

#define SZ 2333333
#define M 2000000
typedef long long ll;
ll p2[SZ];
bool np[SZ];
int ps[SZ],pn=0;
ll f[SZ];
ll MOD=1000000007;
void shai()
{
    np[1]=1; p2[1]=1;
    for(int i=2;i<=M;i++)
    {
        if(!np[i]) {ps[++pn]=i; p2[i]=2;}
        for(int j=1;j<=pn&&i*ps[j]<=M;j++)
        {
            int nx=i*ps[j]; np[nx]=1;
            if(i%ps[j]) p2[nx]=p2[i]*2;
            else {p2[nx]=p2[i]; break;}
        }
    }
    for(int i=1;i<=M;i++) f[i]=(f[i-1]+p2[i])%MOD;
}
ll gs(ll x)
{
    ll ans=0;
    for(ll i=1;i*i<=x;i++) ans+=(x/i-i)*2+1;
    return ans%MOD;
}
ll gf(ll x)
{
    if(x<=M) return f[x];
    ll s=gs(x);
    for(ll t=2;t*t<=x;t++) s-=gf(x/t/t);
    return s%MOD;
}
int main()
{
    shai();
    ll n,ans=0; cin>>n;
    for(ll s=1;s<=n;s=n/(n/s)+1)
    {
        ll ls=n/(n/s);
        ans+=gf(n/s)*(ls-s+1)%MOD;
        ans%=MOD;
    }
    ll aa=(n%MOD)*(n%MOD)%MOD-ans;
    aa=(aa%MOD+MOD)%MOD;
    cout<<aa<<"\n";
}

今天先施工到这。

UPD：辣鸡zzq noip后弃坑了，有心情估计不会再更新这篇文章不然我哪有心情更新新博客QAQ